Die Lichtgeschwindigkeit ist die nieder-dimensionale Grenze
Die Singularität in einem Schwarzen Loch ist die höher-dimensionale Grenze
Mit r_S\space =\space \frac{2\space *\space l_P^2}{\lambda}, ist der Schwarzschildradius direkt mit der Compton-Wellenlänge verbunden
leer
Dimensionale Physik
leer
Theorie zur Vereinigung der Allgemeinen Relativitätstheorie mit den Quantenfeldtheorien
Christian Kosmak, Würzburg 2023 Version 4.1 – 29.05.2023

Bindungsenergie als Schnittmenge von Raumzeitdichte.
5 Wellen und Quanten
leer
Es wird beschrieben, wie eine Quantisierung und eine Wellenbeschreibung entstehen. Dazu wird der dimensionale Übergang benötigt. Die „Seltsamkeiten“ in der QFT kommen fast alle aus dem dimensionalen Übergang ohne Zeit. Für einen ersten Ansatz wird an einer anderen Stelle begonnen und die DK erweitern. Die Gravitationskonstante G soll in der Formel mit der DK allgemeiner aufgebaut werden. Daraus ergibt sich dann ein Zusammenhang, der den dimensionalen Übergang erzeugt.
Dimensionale Konstante (DK) vollständig
Die DK beschreibt ganz allgemein die mögliche Veränderung/Widerstand innerhalb der Raumzeit. Daher muss diese auch eine Beschreibung für DRDs liefern, die nicht der Planck-Masse entsprechen. Im vorhergehenden Kapitel ist die DK in G aus der Beschreibung G\space =\space \frac{l_P}{E}\space *\space c^4 abgeleitet worden. Hier steht E für die Energie der Planck-Masse. Unser Universum ist mit DRD gefüllt, die wesentlich geringeren Energien aufweist. Daher muss der Term der DK um eine Korrektur erweitert werden. Es wird ein Term benötigt, der bei der Planck-Masse keine Auswirkung hat.
Als erstes wird die Definition der Compton-Wellenlänge anders ausgedrückt. Wie bei G stellen wir die Formel um, bis eine klare Aussage enthalten ist. Wir starten wieder mit der Lehrbuchdefinition. Es wird h in Energie mal Planck-Zeit zerlegt. Die Energie wird Planck-Masse mal das Quadrat der LG. Eine LG kürzt sich raus. Die verbleibende LG wird in Planck-Länge durch Planck-Zeit zerlegt.
\lambda_C\space =\space \cfrac{h}{m_C\space *\space c}\space \iff\space \cfrac{m_P\space *\space c^2\space *\space t_P}{m_C\space *\space c}\space \iff\space \cfrac{m_P\space *\space c\space *\space t_P}{m_C}\space \iff\space \cfrac{m_P\space *\space l_P\space *\space t_P}{m_C\space *\space t_P}\space \iff\space \cfrac{m_P}{m_C}\space *\space l_Pm_C\space *\space \lambda_C\space =\space m_P\space *\space l_P
Die Compton-Wellenlänge ist einfach die Planck-Länge mit einem Masseverhältnis multipliziert. Die Compton-Wellenlänge muss direkt mit der Planck-Länge zusammenhängen.
Die gefundene Beziehung wir in die veränderte Formel für G eingesetzt. Hier wird die Energie der Planck-Masse durch m_P\space *\space c^2 ersetzt. Dann die Planck-Masse durch den eben gefundenen Ausdruck.
G\space =\space \cfrac{l_P}{c^2\space *\space m_C}\space *\space \cfrac{l_P}{\lambda_C}\space *\space c^4\space \iff\space \cfrac{l_P}{m _C}\space *\space \cfrac{l_P}{\lambda_C}\space *\space c^2
Nun kann für die Masse eine beliebige DRD angegeben werden. Es muss die zur Masse korrespondierende Compton-Wellenlänge eingesetzt werden. Im Fall der Plack-Masse ist diese die Planck-Länge. Damit hat der zweite Term keine Wirkung. Die DK gibt an, dass für alle Massen, die nicht zu einem SL führen, eine Wellenlänge benötigt wird. Diese Wellenlänge korrespondiert direkt mit der Planck-Länge und der Masse selbst. Je kleiner die Masse, desto größter die Wellenlänge. Damit ist der erste Hinweis gegeben, dass man eine Wellendarstellung zwingend benötigt.
Ergibt sich aus der DK auch eine Quantisierung? Explizit nein! Um dies zu zeigen, wird G in der angegebenen Form in der Berechnung für einen SSR verwendet. M muss mit gleichgesetzt werden.
r_S\space =\space \cfrac{2\space *\space M\space *\space G}{c^2}\space \iff\space \cfrac{2\space *\space M}{c^2}\space *\space \cfrac{l_P}{ m_C}\space *\space \cfrac{l_P}{\lambda_C}\space *\space c^2\space \iff\space \cfrac{2\space *\space l_P^2}{\lambda_C}
\bold{r_S\space =\space \cfrac{2\space *\space l_P^2}{\lambda_C}} Diese kleine Formel ist für die DP wichtig!
Es ergeben sich drei wichtige Aussagen:
- In der Formel r_S\space =\space \frac{2\space *\space l_P^2}{\lambda_C} wird die Wellenlänge λ durch die Wellenlänge für ein SL, die Planck-Länge ersetzt. Dann ergibt dies r_S\space =\space 2\space *\space l_P. Das kleinstmögliche SL, welches sich in unserer Raumzeit bildet, hat einen SSR von mindestens zwei Planck-Längen.
- Nach der Planck-Länge aufgelöst ergibt sich l_P\space =\space \sqrt{\frac{r_S\space *\space \lambda_C}{2}}. Da die Planck-Länge eine Konstante ist, kann weder der SSR (aus ART) noch die Compton-Wellenlänge (aus QFT) null oder unendlich werden. Für beide Größen ist keine Quantisierung enthalten. Über die Planck-Länge erhält man einen Zusammenhang für die Darstellung einer DRD und der Gravitation. Damit ist die Gravitation und die DRD in ihren unterschiedlichen Darstellungen gegenseitig, an dieses Limit gebunden.
- r_S\space =\space 2\space *\space l_P ist in 3D das kleinstmögliche SL. Für die Ruhemasse eines Elektrons, mit der passenden Compton-Wellenlänge, ergibt sich ein SSR von ca. 10^{-57} Dieser SSR kann sich in 3D nicht gebildet haben. Dies gilt für alle Objekte des Standardmodells. Wenn die Gleichung stimmt und es zu jeder Compton-Wellenlänge einen SSR gibt, dann muss sich dieser SSR in einer Raumzeit gebildet haben, welche eine andere Planck-Skala hat. Das Hierarchie Problem ist hier die Lösung. Es wird eine Raumzeit benötigt, bei der sich mit einer kleineren DRD auf einer größeren Länge ein SSR bilden kann. Eine 2D-Raumzeit. Eine 2D-Raumzeit als Fläche lässt sich wesentlich einfacher verändern (DK) als einer 3D-Raumzeit mit Volumen.
Der SSR aus der ART und die Compton-Wellenlänge aus der QFT können gegenseitig ausgetauscht werden. Beide Werte sind nicht quantisiert. Die Compton-Wellenlänge ersetzt die Masse und die Gravitationskonstante gemeinsam für die Berechnung des SSR. Daraus kann man folgern, dass die Compton-Wellenlänge direkt die Veränderung der Raumzeit durch die DRD als Wellendarstellung angibt
Niederdimensionale Darstellung der DRD
Die DRD in 3D hat keine bestimmte geometrische Form. Diese ist einfach eine Dichte. Selbst wenn diese eine Form hätte, könnte wir diese nicht erkennen. Ein Meter bleibt ein Meter. Das gilt nicht nur für die Länge, sondern auch für die geometrische Form. Hier muss nun die letzte Annahme gemacht werden, damit überhaupt etwas erkannt werden kann.
Annahme A-03: Es gibt unendlich viele separate niederdimensionale Raumzeiten.
Unsere Raumzeit ist durch einen Urknall entstanden. Warum dann nicht auch andere Raumzeiten mit unterschiedlicher Anzahl an Raumdimensionen? Das Kopernikanische Prinzip wird allgemein auf Raumzeiten angewendet. Unsere Raumzeit stellt damit keine Besonderheit dar. In unserer Raumzeit passen unendlich viele niederdimensionale Raumzeit. Das Konzept der Quantisierung der Raumzeit, wird hier, in einer komplett anderen Form als Konzept der Separierung der Raumzeit angewendet. Nicht auf den Inhalt einer Raumzeit, sondern auf die Raumzeiten als einzelne Objekte. Jede Raumzeit ist ein separates Objekt für sich.
Damit befindet sich innerhalb einer DRD eine unendliche Menge an niederdimensionale Raumzeiten. Wie im Kapitel Raumzeit-Struktur angegeben, können diese über die Raumdimensionen miteinander verbunden sein. Daraus ergibt sich zwingend, dass die niederdimensionalen Raumzeiten auf die Veränderung der Raumzeitdefinition reagieren müssen. Es gibt grundsätzlich zwei verschiedene Wege, wie diese niederdimensionalen Raumzeiten auf die DRD reagieren können, mit und ohne Ruhemasse.
Wellendarstellung ohne Ruhemasse
Als Beispiel aus dem Standardmodell verwenden wir hier das Photon. Es ist für diese Darstellung in der DP das einfachste Teilchen. Die DRD in 3D kann man sich geometrisch einfach als eine Kugel (Volumen) vorstellen, in der die Raumzeit eine Definition hat, die einer höheren Dichte entspricht. Bleiben wir bei einem Meter. Die Kugel hat einen Durchmesser von einem Meter. Da die Dichte höher ist, nehmen wir an, dass in den Durchmesser insgesamt zwei Meter Länge enthalten sind. Liegt nun eine 2D-Raumzeit in diesen Volumen, so muss diese auf einer Länge von einem Meter zwei Meter unterbringen, ohne eine eigene DRD in 2D zu haben. Die 2D-Raumzeit wird eine transversale Welle ausbilden. Longitudinal geht nicht, da dies in der 2D-Raumzeit wieder eine DRD darstellen würde.
Es werden gleich mehrere Eigenschaften besprochen, welche dann auch für eine Wellendarstellung mit Ruhemasse gelten. Dort kommt nur noch der Unterschied, für eine Wellendarstellung mit Ruhemasse. Diese Welle muss nun folgende Eigenschaften haben:
- Begrenzung im Volumen: Da die DRD eine Ausdehnung hat, so muss die 2D-Welle auch eine Begrenzung erhalten, ab der diese wieder flach ist. Zur „Begrenzung“ kommt nochmals ein Punkt.
- Extrinsisch und intrinsisch: Damit eine extrinsische Welle an der Begrenzung wieder flach werden kann, muss immer ein intrinsischer Anteil vorhanden sein. Der Anteil von extrinsisch zu intrinsisch ist direkt miteinander verbunden. Dieser intrinsische Anteil ist eine 2D-Gravitation und die Schwankung ist eine Schwankung des elektrischen Feldes. Im Standardmodell wird gezeigt, dass ein elektrisches Feld nichts anderes ist als eine 2D-Gravitation, welche von 3D aufgeprägt ist.
- Ausgleich: Die Wellendarstellung gleicht sich selbst in der 2D-Raumzeit direkt aus. Das hat zwei Effekte:
- Das Photon stellt keine Quelle für das elektrische Feld (2D-Gravitation) dar. Es ist nur eine Schwankung. Diese Schwankung der 2D-Gravitation hat nichts mit einer Gravitationswelle in 3D zu tun.
- Die Welle ist vollständig. Es ist zu einem Wellen-Berg auch immer ein Wellen-Tal vorhanden. Die geometrische Darstellung in 2D ist in Summe ausgeglichen. Diese Eigenschaft wird später als Spin bezeichnet. Hier geht es nicht nur um den intrinsischen Anteil, sondern um die generelle Auslegung der Welle aus der Ebene.
- Statisch: Die Welle hat einen intrinsischen Anteil, der direkt als Gravitation angesehen werden kann. Laut der ART, hat die Gravitation in 2D zu wenige Freiheitsgrade, damit sich diese verändern kann. Diese hat wieder zwei Effekte:
- Die Raumkrümmung in 2D kann sich nicht selbstständig bilden. Diese muss immer aus 3D auf 2D „aufgeprägt“ werden.
- Die Raumkrümmung ist statisch, da sich diese nicht verändern kann. Damit ist der extrinsische wie auch der intrinsische Anteil der Raumkrümmung statisch. Eine Ausprägung in 2D bleibt erhalten, wie diese erzeugt wurde. Dies gilt für alle Ausprägungen. Dieses fehlen des Freiheitsgrades ist identisch mit der Energieerhaltung. Keine Änderung in der Zeit für jede geometrische Ausprägung. Es ist nur eine Umwandlung möglich. Dann muss das geometrische Gebilde sich auflösen und neugestaltet werden. Dabei dient die 3D-DRD als Sammeltopf für alle Ausprägungen. Die Sichtweise der QFT, dass sich bei einer WW die Objekte zerstören und neu ausbilden, ist absolut richtig.
- Energieniveau: Die 2D-Raumzeit muss die Kugel der DRD in 3D nicht voll schneiden. Diese könnte auch nur zu einem Teil in dem Volumen der DRD liegen. Dann muss sich eine kleinere Welle in ihrer Ausdehnung und in der Amplitude ausbilden. Der Anteil an DRD auf der 2D-Raumzeit ist geringer. Damit hat eine DRD, als geometrische Ausprägung in einer 2D-Welle, die Möglichkeit das gesamte Energiespektrum zu besitzen.
- Möglichkeiten: Wie man bereits beim Energieniveau erkennen kann, gibt es für die Darstellung der 2D-Welle unendlich viele Möglichkeiten in der Größe und in der Energie. Die 2D-Welle hat auch die Möglichkeit im gesamten Volumen der DRD zu erscheinen. Es können alle 2D-Möglichkeiten gleichzeitig ausgeprägt sein. In 2D existiert die Zeit aus 3D nicht. Damit gibt es für die Darstellungen keine zeitliche Überschneidung. Erst bei der WW würde die DRD auf Grund der 2D-Ausprägungen eine unendliche Energie haben. Dies beschreibt die Renormierung in der QFT. Die mathematische Unendlichkeit für alle WW zur gleichen Zeit ist tatsächlich nicht relevant. Nur eine WW verbindet die 2D-Möglichkeit in der Zeit mit der 3D-DRD. Dieser Teil ist dann die Bobachtung. Alle Möglichkeiten in 2D können sich aber gegenseitig als Summe in 3D beeinflussen. Diese sind alle tatsächlich vorhanden.
- Die DRD gibt die gesamte Menge an Energie für die Möglichkeiten vor. Diese Möglichkeiten liegen alle in 2D. Die Möglichkeiten (virtuellen Teilchen) haben keine Auswirkung auf die Gravitation in 3D, das hat nur die DRD in 3D selbst.
- Der Weg von den möglichen zur einzigen Ausprägung wird im Abschnitt „Superposition, Wahrscheinlichkeit und Kollaps“ beschrieben.
- Begrenzung in der Raumzeit: Eine Welle darf laut QFT im gesamten Universum auftreten und nicht nur in dem Volumen der DRD. Das ist vollkommen richtig. Da die DRD eine Dichte der Raumzeit selbst ist und es keinen Raumzeitpunkt mit der Energie von null geben kann, hat die Welle die Möglichkeit die gesamte Raumzeit als Aufenthaltsort zu nutzen. Eine DRD hat keine Grenze mit einer absoluten Null-Energie, außer die Grenze der Raumzeit selbst. Daher ist die gesamte Raumzeit erlaubt und nicht nur das Volumen der DRD. Die Wahrscheinlichkeit für eine WW außerhalb des 3D-DRD Volumen ist einfach nur sehr gering. Damit hat die 2D-DRD theoretisch die gesamte Raumzeit zur Verfügung, selbst wenn die DRD für die Gravitation in 3D klar lokalisiert ist. Die Fragestellung, wie passt das räumlich nicht 100% bestimmte Verhalten und die Gravitation zusammen ist damit gelöst. Das Problem existiert in der DP nicht.
- Wellenlänge für die Energie: Zur Beschreibung des Energieinhalts einer DRD reicht die Wellenlänge aus. Diese wurde auch für die DK benutzt. Warum nicht die Amplitude? Eine Wellenlänge gibt immer die Energie in einer DRD an. Wenn man die Amplitude erhöht, vergrößert sich automatisch das Volumen. So kommt keine höhere Energie zustande. Wenn der Energieinhalt einer DRD vergleichen werden soll, muss das Volumen konstant gehalten werden. Dann ist die Menge an 2D-Raumzeit, von einer Welle in dem Volumen, nur durch die Wellenlänge bestimmt. Mehr Raumzeit in einem Volumen ist eine höhere DRD.
- Amplitude für die Wahrscheinlichkeit: Will man in dem Volumen einer DRD eine WW erzeugen, so muss man eine Ausprägung der Möglichkeiten tatsächlich (physisch) treffen. Da sich immer 2D mit 2D trifft, ist nicht das Volumen, sondern die Fläche entscheidend. Dabei spielt die 2D-Ebene, aus der die Amplitude hervorgeht, keine Rolle. Nur die Auslenkung der Welle ist die Ausprägung der DRD und ist relevant. Die Auslenkung der Welle kann geometrisch immer als Kreis aufgefasst werden. Die Fläche des Kreises ist bei jeder Welle . Die Kreiszahl π ist bei allen möglichen Ausprägungen gleich. Nur der Radius unterscheidet sich. Daher ist das Quadrat der Amplitude für die „Trefferwahrscheinlichkeit“ die einzige wichtige Größe. Da es Wellen sind (Berg und Tal), wird die Welle mit der größten Fläche nicht immer getroffen. Selbst Wellen mit einer kleinen Amplitude können getroffen werden.
Da es im Standardmodell nur das Photon und das Gluon ohne Masse gibt, hier ein kurzer Vorgriff auf das Standardmodell. Beim Gluon liegt die Auslegung einer Welle auf 2 verschiedenen 2D-Raumzeiten. Hat den Spin 1, da sich über die 2D-Raumzeiten hinweg, aus Sicht von 3D, alles ausgleicht. Ist aber zugleich Träger der Ladung, da in der jeweiligen 2D-Raumzeit nur ein Teil der Welle liegt. Damit hat ein Gluon immer eine positive und eine negative Ladung. Die Reichweite ist, obwohl keine Ruhemasse, sehr gering. Die Welle liegt auf zwei verschiedenen Ebenen und hat keine eindeutige Richtung für den Impuls. Ein Gluon kommt aus der Überlagerung der DRD, welche die Quarks im Atomkern erzeugt, nicht raus.
Wellendarstellung mit Ruhemasse
Die zweite Möglichkeit, wie sich eine DRD auf 2D überträgt ist, dass in der 2D-Raumzeit direkt eine DRD aufgeprägt wird. Bei dieser Abbildung muss man aufpassen, mit welchen Werten gerechnet wird. Die Planck-Skala in 2D ist eine andere. Die DK war bis jetzt für unsere 3D-Raumzeit ausgelegt. In 2D müssen diese Werte unterschiedlich sein. Auf Grund des Hierarchie Problems ist klar, dass sich eine 2D-Raumzeit wesentlich leichter stauchen oder dehnen lässt als eine 3D-Raumzeit. Auf eine größere Länge muss eine kleinere Energie den höherdimensionalen Übergang auslösen. In 2D wird mit einer sehr kleinen Masse ein SL mit großen SSR erzeugt (im Verhältnis zur Planck-Skala in 3D).
Über die dimensionale Grenze bleiben als Größe nur die LG und die Compton-Wellenlänge erhalten. Die LG definiert sich über das Stauchen einer einzelnen Raumdimension. Dies ist in 3D zu 2D identisch. Die Compton-Wellenlänge kommt aus der Verbindung der Raumdimensionen und muss die gleiche Länge haben. Alle anderen Größen sind unterschiedlich. Daher kann man nicht einfach von 3D in 2D „hineinrechnen“.
Sobald man die DRD der Ruhemasse eines Elektrons hat, reicht diese aus, um in 2D ein SL zu erzeugen. Die Masse in 3D ist nicht die gleiche Masse aus Sich in 2D, da die Anzahl der beteiligten Raumdimensionen an der Masse unterschiedlich ist. Dieses SL kann sich laut ART in 2D durch eine reine intrinsische Abbildung nicht bilden. Es wird wieder eine extrinsische Abbildung benötigt. In 3D könnte man im Volumen der DRD sonst nichts feststellen. Durch das SL bekommt die 2D-Abbildung einen höherdimensionalen Übergang und belegt in 3D wieder alle Raumdimensionen. Der Trick ist, dass eine 2D-Abbildung durch die Singularität in einem SL alle Raumdimensionen in 3D belegt und damit eine Ruhemasse hat.
Die Darstellung ist aber keine volle Welle. Diese entspricht dem angegebenen Bild. Dies wird gern benutzt, um die Gravitation in 3D zu erklären. Dort ist das Bild falsch. Es zeigt explizit eine Mischung aus extrinsischer und intrinsischer Raumkrümmung. In 3D falsch, in 2D genau richtig.
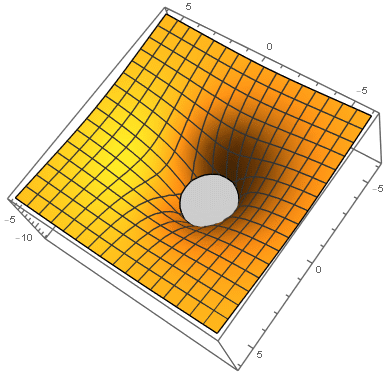
Es ist aus der Sicht einer Wellendarstellung nur eine halbe Welle. Daher ist der Spin nur ½ für diese Abbildung. Da sich die Abbildung in 2D nicht ausgleicht, ist das Raumvolumen „belegt“. Es können keine zwei gleichen Abbildungen dieser Art in das gleiche Raumvolumen gebracht werden. Das SL erzeugt ein konstantes Gravitationsfeld in 2D. Daher hat ein Elektron ein elektrisches Feld und ist die Quelle des Feldes. Genauere Erklärung beim Standardmodell.
Quantisierung
Die Quantisierung hat allgemein zwei Merkmale. Einmal gibt es Energien tatsächlich nur in bestimmten Stufen und ein anderes Mal kann die Energie beliebig sein, die Energie muss aber immer vollständig oder gar nicht in eine WW eingehen.
Der einfachere Teil ist Alles oder Nichts in der WW. Die DRD-Ausprägungen sind immer in 2D. Dort in unterschiedlichen Raumzeiten. Raumzeiten können gegenseitig nichts „abschneiden“. Weder 3D zu 2D noch 2D untereinander. Das geht insbesondere nicht, da die Zeit nicht geteilt wird. Eine WW kann nicht nach der „halben Zeit“ aufhören. Hier ist 3D der „Sammeltopf“ für alle niederdimensionale Ausprägungen. Es geht alles rein und wird in der WW wieder alles ausgeteilt.
Für die Quantisierung, dass die DRD-Ausprägung selbst nur bestimmte Stufen einnehmen kann, ist wieder die niederdimensionale Ausprägung verantwortlich. Ob halbe oder ganze Welle, die Darstellung ist immer eine Welle. Sonst ist im 3D Volumen eine 2D Ausprägung nicht erkennbar. Nun muss die Welle bei null starten und enden. Das Volumen könnte sich nur ändern, wenn sich die Amplitude ändern würde. Diese ist aber durch die WW festgelegt. Damit kann in dieses Volumen nur noch eine halbe oder eine volle Welle eingebracht werden. Daraus folgt, dass die Darstellungen in 2D selbst einen Potentialtopf bilden. In 3D allein gibt es keinen Grund für eine Quantisierung. Diese erfolgt nur über den dimensionalen Übergang.
In der DP werden zusätzlich zur Raumzeit keine weiteren Felder benötigt. Der Unterschied liegt nur in den jeweiligen geometrischen Ausprägungen in den verschiedenen Raumdimensionen. Dazu im Kapitel Standardmodell mehr.
Superposition, Wahrscheinlichkeit und Kollaps
Da es unendlich viele niederdimensionale Raumzeiten gibt kann es unendlich viele Ausprägungen für eine einzelne DRD geben. Unendlich viele reale Ausprägungen aus den niederdimensionalen ergibt eine unendliche Energie. Das wird nicht beobachtet. Hier ist es wichtig, sich nochmals in Erinnerung zu rufen, dass die DRD selbst in 3D mit einer konkreten Ausprägung liegt. Im niederdimensionalen hat die DRD unendlich viele Möglichkeiten einer realen Ausprägung. Die DRD hat im ersten Ansatz keinen Grund sich für eine Ausprägung zu entscheiden. Solange keine konkrete Ausprägung ausgewählt ist, existieren alle Möglichkeiten im Niederdimensionalen aus 3D-Sicht gleichzeitig. Die Raumzeiten sind mit dem Raum und nicht mit der Raumzeit verbunden. Es existiert kein zeitliches Problem, dass alle Ausprägungen zu jedem Zeitpunkt möglich sind. Damit ist die Darstellung der DRD im niederdimensionalen eine Superposition aller möglichen Ausprägungen für alle möglichen Zustände. Erst mit einer WW muss für die passende Geometrie der WW eine Ausprägung mit 3D verbunden werden. Wenn sich mindestens zwei 2D-Ausprägungen gegenseitig beeinfluss wollen, geht dies nur in 3D. Man kann daher nur mit einer Wahrscheinlichkeit eine spezielle Abbildung aus allen möglichen Abbildungen erhalten.
Eine WW hat eine konkrete Geometrie. Zum Beispiel ist das Photon eine transversale 2D Welle der Raumzeit selbst. Hat eine DRD für diese Geometrie keine mögliche Ausprägung, so kann diese an der WW nicht teilnehmen, hier z.B. eine Fläche. Die Möglichkeiten müssen sich auf eine konkrete Ausprägung dieser Geometrie festlegen. Die WW als DRD überlappt sich mit einer anderen DRD und muss darauf reagieren. Die DRD nimmt die WW auf und erzeugt einen neuen Zustand. Die Festlegung passiert im Sammeltopf 3D und ist damit kein Prozess im Niederdimensionalen. Daher kann zum Beispiel die Schrödinger-Gleichung den “Wellenkollaps” nicht beschreiben. Die 3D-Festlegung muss nur innerhalb der, durch die WW geforderten Geometrie, eindeutig sein. Daher sind bei einem Teilchen nur die Eigenschaften festgelegt, welche durch die WW vorgegeben sind.
Ist die Festlegung der Eigenschaft über eine Information an den 3D Raum gebunden, so ist diese Eigenschaft Teil der 3D-DRD und kann sich nicht sofort wieder ändern. Wird eine bestimmte Geometrie (“Eigenschaft”) festgestellt, so wird bei einer zweiten Messung diese Geometrie wieder beobachtet.
Verschränkung
Die Verschränkung lässt sich in der DP sehr leicht verstehen. Der entscheidende Gedanke dazu ist, dass eine Verschränkung kein Austausch von DRD in der 3D Raumzeit darstellt.
Eine WW wird durch eine DRD in 3D ausgelöst. Die WW selbst ist eine DRD, welche in der 3D Raumzeit vorhanden ist. Nur auf dieser Ebene lässt sich die Verschränkung nicht verstehen. Eine DRD hat eine Ausprägung und damit Eigenschaft im Niederdimensionalen. Zwei verschiedenen Objekte mit der gleichen Wellenfunktion haben diese Eigenschaft in der gleichen niederdimensionalen Geometrie. Damit ist aus Sicht von 3D und von 2D in der Wellenbeschreibung keine Unterscheidung mehr möglich. Diese Ausprägungen müssen mit einer einzigen Wellenfunktion beschrieben werden. Diese Objekte können in 3D in einer beliebigen Zeit auf eine beliebige Distanz gebracht werden. Diese Raumzeit existiert für die gemeinsame niederdimensionale Geometrie nicht.
Für eine Verschränkung lassen sie daher die folgenden zwingende Schlüsse ziehen:
- Verschränkung ist niederdimensional, eine WW ist mit der 3D Raumzeit verbunden. Daher wird bei der Verschränkung keine WW in 3D ausgetauscht.
- Da die Verschränkung die 3D-Raumzeit nicht kennt muss jede Veränderung an der niederdimensionalen Geometrie instantan im gesamten 3D Universum passieren. Es ist explizit keine Verzögerung möglich.
- Da nur die Eigenschaft im niederdimensionalen liegt und eine Information an eine 3D Raumzeit gebunden ist, kann niemals eine Information schneller als die LG über eine Verschränkung übertragen werden.
Das Problem der „Spukhaften Fernwirkung“ existiert nicht, da für die Wellenbeschreibung der verschränkten Objekte kein „Fern“ vorhanden ist.
Unbestimmtheit
Für eine Erklärung, woher die Unbestimmtheit kommt, wird das klassische Beispiel mit Impuls und Ort (\Delta p\space *\space \Delta x) benutzt. Der Impuls ist eine direkte Dichte in der Raumzeit. Wenn eine Dichte gemessen werden soll, so benötigt man zwingend ein Volumen/Strecke. Wird das Volumen kleiner gemacht, um den Ort besser zu bestimmen, so wird die Dichte im Verhältnis zum Rest immer schlechter feststellbar sein. Will man im Gegensatz die Dichte exakt feststellen, so müsste man dies im Verhältnis zum gesamten Rest machen. Der Rest ist in diesem Fall die Raumzeit selbst.
Für diese Messung ist die benötigte Menge an Raumzeit gegenläufig. Daher kommt man nicht unter ein bestimmtes Limit bei der Messung hinaus. Da in der DP alles eine Abbildung in der Raumzeit ist können nur wenige Kombinationen von Messungen exakt durchgeführt werden. Die Unbestimmtheit ist schon auf Grund der Definition der DRD als Raumdichte enthalten.
Vakuumfluktuation
In der DP kann es ein echtes Vakuum mit dem Energieinhalt null nicht geben. An jedem Punkt der Raumzeit ist allein durch die Existenz des Raumpunktes eine “Raumdichte” und damit eine von null verschiedene DRD gegeben. Ein Raumpunkt ohne zusätzliche DRD wird einfach als das Null-Niveau des Vakuums festgelegt. Im Vakuum ist immer DRD/Energie vorhanden, weil immer eine Raumzeit vorhanden ist.
In der QFT hat jeder Raumpunkt auf Grund seiner Vakuumenergie und der Unbestimmtheit eine Vakuumfluktuation. Hier ergibt sich eine Differenz in der Sichtweise zwischen QFT und DP. Damit auch eine unterschiedliche Aussage zur Vakuumfluktuation. In der QFT darf der Wert null, auf Grund der Unbestimmtheit nicht exakt erreicht werden. Der Wert darf positiv, wie negativ von Null abweichen, aber nicht exakt null werden. In der DP ist keine null erreichbar, da ein Raumpunkt vorhanden ist. Es ist nicht möglich von der positiven Energie auf die Null zu kommen. Es ist in diesem Kapitel beschrieben, dass die DRD einen Grund, in Form einer WW (Geometrie) zischen DRDs benötigt, um von der Wahrscheinlichkeitsaussage zu einer konkreten Ausprägung der Geometrie zu kommen. In der DP verbleibt der Raumpunkt in der Superposition und erzeugt damit keine Fluktuation. Es wird ein “Anreiz/Geometrie” benötigt. In der DP tritt nur dann eine Fluktuation auf, wenn bereits eine DRD mit mindestens einer geometrischen Ausprägung vorhanden ist. Gravitation löst keine Fluktuation aus, da diese in 3D liegt und keine Geometrie für 2D beinhaltet.
Fluktuation tritt nur auf, wenn eine DRD vorhanden ist. Der Unterschied von DP und QFT kann nicht durch eine direkte Messung festgestellt werden (Casimir-Effekt), da bei einer Messung immer eine DRD da ist. Indirekt ist dies evtl. durch die Vakuumenergie der gesamten Raumzeit möglich. Siehe dazu Kapitel Kosmologie.
Hilbertraum und QFT
Da die DRD eine geometrische Abbildung besitzt ist ein Vektorraum eine passende mathematische Grundlage für die Beschreibung. Wird genau eine geometrische Ausprägung gewählt, kann von den anderen Möglichkeiten keine mehr einen Anteil haben. Damit ist der Vektorraum zwingend orthogonal und das Skalarprodukt muss definiert sein.
Will man von einer Zustandsbeschreibung auf eine andere Zustandsbeschreibung wechseln, so haben diese die gleiche geometrische Grundlage. Diese geometrische Ausprägung darf sich nicht ändern, da diese die DRD definiert. Damit muss dieser Operator zwingend unitär sein.
Es muss einen Untervektorraum geben, da die Geometrie nicht bei jeder WW vollständig bestimmt ist. Je stärker die Geometrie festgelegt werden soll, umso mehr Information wird in der Wellengleichungen benötigt. Für jede mögliche einzelne Geometrie. Man kommt von der Schrödinger-Gleichung zur Pauli-Gleichung und dann zur Dirac-Gleichung.
Die Schrödinger-Gleichung muss eine komplexe Darstellung haben. Die beschriebene Welle hat in 3D und im Niederdimensionalen eine Ausprägung. Daher braucht man zwei verschiedene “Ebenen” der Darstellung in einer Gleichung. Das bringen die komplexen Zahlen mit.
In der QFT werden durch die Operatoren die Objekte erzeugt und vernichtet. Das entspricht der realen Darstellung besser als die Operatoren in der Quantenmechanik. Grund ist, dass die DRD in 3D liegt und die WW und das Objekt in diesen “Sammeltopf” einzahlen und sich ein neues Objekt mit den veränderten Eigenschaften bildet. Die 3D-DRD stellt den “Vermittler” zwischen den niederdimensionalen Abbildungen da.
Die Methode des Pfadintegrals in der QFT ist die richtige mathematische Berechnung für ein beliebiges Teilchen. Die niederdimensionale Ausprägung ist über den Raum und nicht der Raumzeit verbunden. Ein Teilchen hat damit „unendlich“ Zeit tatsächlich alles zu machen. Zusätzlich besitzt diese DRD alle möglichen niederdimensionale Raumzeiten für eine Bewegung in der eigenen Raumzeit. So verrückt die Idee auch klingen mag. Das Teilchen kann, ohne eine Einschränkung in 3D (z.B. eine Mauer), die gesamte 3D-Raumzeit in “Null-Zeit“ austesten. Nur die Summe aller Möglichkeiten muss sich dann wieder an die Begrenzungen aus 3D halten.
Die Quantenmechanik und die OFT sind tatsächlich die physikalisch richtigen Beschreibungen für die reale Darstellung. Es ist nicht nur ein mathematisches Hilfskonstrukt, dass das passende Ergebnis liefert.
Kontakt, Download und weitere Links
Mitarbeit, Kritik, Anregungen und Fragen – Kontakt per Mail
DP komplett als PDF – Version 4.1 vom 30.05.2023
English: DP complete as PDF – Version 4.1 from 30.05.2023
YouTube Kanal zur Dimensionalen Physik
Aufzeichnung Vortrag bei DPG Frühjahrsveranstaltung Dresden 20.03.2023
leer