
Alles besteht aus Raumzeit
Es sollte inzwischen allgemein bekannt sein, dass die QM für die Voraussage zu einer Messung, nur eine Aussage zur Wahrscheinlichkeit des Messergebnisses erzeugen kann. Das ist wie bei Unschärfe und Verschränkung nicht als Grundkonzept eingebaut. Das hat sich erst später herausgestellt. Tatsächlich wurde die Schrödingergleichung an Anfang anders interpretiert. Erst die sogenannte Bornsche Wahrscheinlichkeitsinterpretation (Regel) hat die Lösung gebracht. Damit war klar, obwohl man alle Information zur Schrödingergleichung hat, kommt da nichts Genaueres als eine Wahrscheinlichkeit heraus. Es ist nicht so, als ob da weitere Informationen gesammelt werden müssen, um eine exakte Aussage treffen zu können. Es ist bereits im Grundsatz nicht möglich eine andere Information als eine Wahrscheinlichkeit aus der QM zu erhalten.
Wir haben schon festgestellt, dass Einstein mit der Verschränkung seine Probleme hatte. Die Wahrscheinlichkeitsinterpretation war der zweite Punkt. Einstein schrieb an Max Born 1926: „Die Quantenmechanik ist sehr achtungsgebietend. Aber eine innere Stimme sagt mir, dass das doch nicht der wahre Jacob ist. Die Theorie liefert viel, aber dem Geheimnis des Alten bringt sie uns kaum näher. Ich bin überzeugt, dass der nicht würfelt.“ Bei der Verschränkung kommen wir auf eine gemeinsame Lösung zwischen der QM und Einstein. Bei der Wahrscheinlichkeit müssen wir uns aber komplett auf die Seite der QM schlagen. Wir werden sehen, dass wir auf Grund unseres Ansatzes, nur eine Wahrscheinlichkeit erhalten können.
Nur bei einem speziellen Aufbau eines Experimentes erhalten wir eine eindeutige Aussage zu einem Messergebnis. Wenn wir bei einer Messung einen Wert festgestellt haben und direkt anschließend diese Messung wiederholen, so erhalten wir mit 100% Wahrscheinlichkeit das identische Messergebnis wieder. Warum dies so ist, klären wir beim Doppelspaltexperiment. Der „Wellenkollaps“ bei der Messung ist hier noch kein Thema. Hier geht es darum, warum es nur Wahrscheinlichkeiten gibt und warum diese eine Gewichtung haben.
Für die QM brauchen wir, rein für die Wahrscheinlichkeit, nur zwei Grundelemente:
Ob die Schrödingergleichung und damit die Wahrscheinlichkeit nur eine Berechnung oder auch eine physikalische Abbildung ist, ist ein beliebtes Thema in den Interpretationen der QM. Wir weichen von der Kopenhagener Interpretation ab und behaupten, dass die Wahrscheinlichkeit eindeutig eine physikalische Abbildung hat und nicht nur eine Rechengröße ist. Damit müssen die zwei Grundelemente eine direkte Abbildung in der Raumzeit haben. Allerdings ist dies bei den Möglichkeiten und der Gewichtung anders ausgeprägt.
Für die Möglichkeiten benutzen wir die identische Grundlage wie bei der Superposition. In jeden n-dimensionalen Raumzeitvolumen einer Raumzeitdichte gibt es unendlich viele (n-1)-dimensionale Raumzeiten und damit Raumzeitvolumen und Raumzeitdichten.
Dabei kann eine einzelne Möglichkeit sich selbst nicht verändern. In der Kosmologie haben wir erkannt, dass wir bei nur zwei Raumdimensionen ausschließlich statische Abbildung erzeugen können. In der QM werden wir diese statischen Abbildungen später „stationäre Zustände“ oder „Pfade“ nennen. Die Erzeugung der Abbildung war in der Kosmologie ein Urknall, in der QM wird dies Erzeugung oder Vernichtung genannt. Dann hat sich aber in der Abbildung in 3D durch eine Wechselwirkung etwas verändert. In 2D bleibt alles erstmal statisch. Wenn es um Teilchen geht, so werden diese 2D Abbildungen „virtuelle Teilchen“ genannt. Vorhanden, aber in 3D nicht feststellbar, da die Abbildung in 2D liegt.
Wichtig: Es sind immer unendlich viele Möglichkeiten. Beim Beispiel mit dem Ort in der Superposition ist dies klar. Aber wie ist es beim Spin? Da messen wir doch nur Spin up und Spin down. Das sind nur zwei Möglichkeiten. Hier müssen wir aufpassen. Auch beim Spin ist die Richtung immer vollständig beliebig. Wenn wir den Spin messen wollen, so suchen wir uns eine vollkommen frei wählbare Achse zu dieser Messung aus. Bezogen zu dieser Achse hat der Spint die Eigenschaft up oder down. Die Messung kann sich aber auf alle beliebigen Richtungen (Achsen) beziehen. Durch die Frage/Messung, die wir an das System stellen, teilen wir alle Möglichkeiten in up und down auf. Es bleiben aber unendlich viele Möglichkeiten.
Bei der Messung werden wir dann sehen, dass sich die Möglichkeiten gegenseitig bedingen können. Das wird beim Doppelspalt für die Teilchen das Interferenzmuster ergeben. Auf dem Schirm werden aber immer nur ganz konkrete Orte für die einzelne Wechselwirkung angezeigt. Das heißt, bei der Wechselwirkung wird immer nur eine Möglichkeit „gezogen“. Daher kommt die Idee mit dem Wellen-Teilchen-Dualismus. Wir werden zeigen, dass es diesen Dualismus nicht gibt. Ein Teilchen ist eine Raumzeitdichte mit einem Volumen und kein Punkt. Ein Teilchen ist aber auch keine Welle. Das Verteilen und gegenseitige Beeinflussen sind viele verschiedene einzelne Abbildungen. Diesen niederdimensionalen Abbildungen kann man keinen eindeutigen Ort in 3D zuweisen. Wir müssen den Wellen-Teilchen-Dualismus nicht erklären, dieser existiert so nicht. In der DP haben wir einen Dualismus, der eine gleichzeitige Abbildung in 3D und in 2D ist. Wir haben keinen Punkt und keine Welle. Wir werden aber bei der Gewichtung sehen, dass die mathematische Wellenbeschreibung eine sehr gute Analogie für dieses Verhalten ist.
Bei der Gewichtung gibt es zwei verschiedene Arten von Gewichtungen. Bei der einen Gewichtung ist diese von Eigenschaften des Teilchens abhängig und bei der anderen nicht.
Machen wir erst das Beispiel mit dem Spin, dass ist einfacher. Beim Spin gibt es eigentlich keine Gewichtung. Das wir immer ein 50:50 Wahrscheinlichkeit von Spin up und Spin down erhalten, liegt an der Fragestellung. Es sind alle Richtungen mit einer identischen Gewichtung vorhanden. Durch die Fragestellung von Spin up und Spin down zu einer bestimmten Achse, teilen wir diese Menge in zwei gleiche Portionen auf. Das Ergebnis sollte uns nicht überraschen. Dies bedeutet aber auch, dass der Spin ein Merkmal sein muss, der zu den geometrischen Ausprägungen in 2D gehört. Diese können wir aus 3D heraus nicht unterscheiden und sind für uns immer gleich. Damit ist eigentlich keine Gewichtung vorhanden. Nur die Gewichtung, welche wir durch die Fragestellung einbringen.
Jetzt nehmen wir wieder unser Elektron, welches wir von uns weg beschleunigen. Da sieht die Sache anders aus. Das Elektron wird mit einer sehr hohen Wahrscheinlichkeit den geraden Weg beschreiten. Es hat aber eine geringe Wahrscheinlichkeit, die nicht null ist, dass es vom geraden Weg abweicht. Je größer die Abweichung, desto geringer die Wahrscheinlichkeit. Hier gibt es Unterschiede. Wenn ich mich als Mensch in gerader Richtung in Bewegung setze, dann darf ich die Wahrscheinlichkeit für eine Abweichung getrost auf null setzen. Das liegt an meiner Masse. Eine spezielle Eigenschaft des Objektes. An diesem Punkte bestehe ich darauf, dass dies nur am sehr großen Verhältnis der Masse von mir zum Elektron liegt, wie bei jedem andern Menschen auch. Selbst wenn meine Frau, zu meiner Eigenschaft der Masse, wahrscheinlich etwas anderes behaupten würde.
Hier ist die Gewichtung der Wahrscheinlichkeit an einer Eigenschaft gebunden, der Masse. Masse ist aber nur eine Form der Raumzeitdichte. Aus der Superposition wissen wir, dass alle möglichen 2D Ausprägungen jeweils separate 2D Raumzeiten sind. Diese müssen sich mit der 3D Raumzeitdichte räumlich überlagern. Da alle n-dimensionale Raumzeiten immer kontinuierliche sind, gibt es an jedem Raumzeitpunkt unserer Raumzeit eine Überlagerung. Damit wäre jeder Raumzeitpunkt mit der identischen Gewichtung versehen. Die Raumzeitdichte spielt jetzt den entscheidenden Faktor. Wir werden das Elektron eher dort finden, wo in 3D die 2D Raumzeitdichte dem Elektron am besten entspricht.
Damit ist im Mittel das Elektron am ehesten dort zu finden, wo auch die 3D Raumzeitdichte liegt. Die Abbildungen der Raumzeitdichten von 3D und 2D überlagern sich dort an stärksten. Hier kommt die Wellenabbildung ins Spiel. Wir haben nur kontinuierliche Raumzeiten. Wenn wir in 3D von 2D etwas erkennen wollen, dann fast nur über die extrinsischen geometrischen Ausprägungen in 2D. Damit ist die Wellenabbildung einfach passend. Die verschiedenen geometrische Abbildungen in 2D können sich nun an bestimmten Orten in 3D damit verstärken oder abschwächen. Das Elektron wird man wohl am meisten an den Orten feststellen können, wo die Verstärkung am größten ist. Das klären wir aber am Doppelspalt genauer. Die Wahrscheinlichkeit für das Elektron ist im Mittel genau dort am größten, wo auch die 3D Raumzeitdichte liegt. Bei den Abweichungen spielen die Interferenzen aus den „Wellen“ eine Rolle.
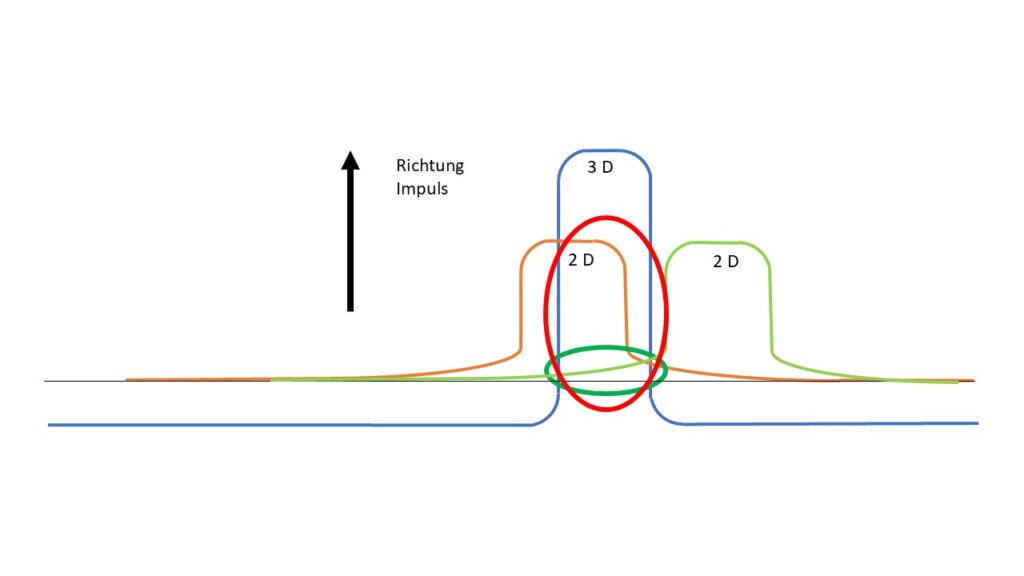
Die Amplitude soll die Richtung des Impulses darstellen. Die Welle von links in Orange hat die größte Schnittmenge mit der 3D Raumzeitdichte und daher mit größerer Wahrscheinlichkeit gemessen zu werden, als die Welle von rechts in Grün. Die Schnittmengen in den Kreisen ist die Wahrscheinlichkeit.
In dem Bild erkennen wir, wo die Überschneidung in der 3D Raumzeitdichte am größten ist. Dort wird das Teilchen im Mittel, über eine Wechselwirkung aus 2D heraus, am häufigsten anzutreffen sein. Je größer der Unterschied der Wellenamplitude, desto geringer ist die Wahrscheinlichkeit. Da bei einem Objekt, wie einem Menschen, die Amplitude der Raumzeitdichte in 3D ca. um den Faktor größer ausfällt als bei einem Elektron, ist eine Abweichung mit null gleichzusetzen. Daher erkennen wir im Alltagsleben nur eine Klassische Mechanik und keine Quantenmechanik.
Als gute Analogie für die Wahrscheinlichkeiten nehmen wir eine Urne mit Kugeln. Eine verdammt große Urne mit unendlich vielen Kugeln. Naja, es muss einen Vorteil haben Physik theoretische betreiben zu können.
Beim Spin sind in der Urne identisch Kugeln mit der Unterscheidung der Farbe. Sagen wir Weiß und Schwarz. Dann ist es klar, dass wir nach sehr vielen Entnahmen aus der Urne eine nahezu identische Menge an weißen und schwarzen Kugeln gezogen haben.
Beim Ort des Elektrons, hat jeder Raumzeitpunkt in 3D eine Kugel. Der Raumzeitpunkt mit der größten Übereinstimmung der Raumzeitdichte von 3D zu 2D hat die größte Kugel. Damit wird diese wahrscheinlicher gezogen als eine andere. Die Wahrscheinlichkeit für die anderen sind aber niemals null. Diese sind in der Urne vorhanden. Wenn sich die 2D Raumzeitdichten sich gegenseitig beeinflussen, so wird eine Kugel größer und im umgekehrten Fall kleiner.
Das Wellenbild ist etwas einfacher. Wenn wir von oben in die Urne reingreifen, dann werden wird am ehesten die Raumzeitdichte ziehen, welche die größte Amplitude hat und damit am meisten noch oben reicht.
Die Argumentation über die Raumzeitdichte hilft bei einem weiteren Fall zur Wahrscheinlichkeit. Wir werden später das Doppelspaltexperiment besprechen. Das hat man bereits mit größeren Objekten durchgeführt. Sehr bekannt ist dies mit C60 Buggy-Balls. Ein Molekül aus 60 Kohlenstoffatomen. Warum erhalten wir am Doppelspalt keine Interferenzen für 60 separate Kohlenstoffatome, sondern für ein C60-Molekül. Die Wahrscheinlichkeit für den Ort muss auf das gesamte Gebilde übergehen und nicht auf die Bestandteile. Wir müssen in unserem Beispiel von Elektron bis zum Menschen kommen.
Der Grund dafür ist wie immer Raumzeitdichte in einer kontinuierlichen Raumzeit. Damit überlagert sich die Raumzeitdichte bereits in 3D und wir erhalten eine Wahrscheinlichkeit für die gesamte überlagerte Raumzeitdichte in 3D.
Wir werden sehen, dass dies auch der Grund ist, warum es sowas wie eine „Quasi-Teilchen“ in der QM geben kann. Ihr seht, für eine funktionierende QM kommen wir an einer kontinuierlichen Raumzeit einfach nicht vorbei.
Hier das Gleiche wie bei der Verschränkung. Das wir eine Wahrscheinlichkeit erhalten ist bereits beim Ansatz für die Superposition mit drin. Wir haben unendlich viele Möglichkeiten in den niederdimensionalen Raumzeitkonfigurationen. Die Überraschung ist wohl eher, warum wir immer nur eine davon in 3D erhalten können. Da kommt unser h mit der Schnittstelle ins Spiel. Wir haben nur die Energie aus 3D Raumzeitdichte zur Verfügung. Eine Möglichkeit wird bei der Messung mit 3D interagieren. Welche es wird, ist vorab nicht bestimmbar. Damit ist zur Wahrscheinlichkeit schon fast alles gesagt. Wie die gegenseitige Beeinflussung der Wahrscheinlichkeiten läuft (die Interferenz der Wellen), machen wir im späteren Kapitel zur Mathematik der QM.
Durch unseren Ansatz, ist das oft „merkwürdige“ Verhalten der QM sehr leicht erklärbar.