
Alles besteht aus Raumzeit
Die SRT basiert auf nur 2 Prinzipien
Das klingt doch sehr einfach. Ist es auch. Wir werden hier die Dinge trotzdem entgegen dem Lehrbuchansatz anschauen müssen. Mit der DP haben wir einen für das Relativitätsprinzip wichtigen Aspekt verschoben. Es sieht so aus, dass eine Raumzeitdichte und damit auch der Bewegungszustand einen „absoluten“ Wert hat. Wir werden sehen, dass wir in der DP keinen absoluten Wert erhalten können. Allerdings ist eine Information von kleiner und größer zwischen Bewegungszuständen vorhanden. Laut dem Lehrbuchansatz des Relativitätsprinzips ist, das nicht erlaubt. Jedes Objekt kann sich als in Ruhe betrachten und es darf kein kleiner oder größer geben. Schon das Wort „Bewegungszustand“ ist dort nicht richtig. Dieser hängt immer vom gewählten Bezugssystem ab. Man kann einem Objekt keinen Zustand in der Bewegung eindeutig zuordnen. Doch, genau das werden wir. Um noch einen obendrauf zu legen, werden wir das Relativitätsprinzip für alles, was im Universum existiert, zwingend daraus erzeugen. Wir dürfen das Relativitätsprinzip nicht einfach als Postulat akzeptieren. Das müssen wir sauber begründen. Klingt doch spannend.
Es kommt dann immer das Gegenargument, dass die DP eine Art von Lorentz-Äther-Theorie ist. Hier ist wichtig, dass wir nie einen Äther benutzen. Es gibt nur Raumzeit. Ein zusätzlicher Äther in irgendeiner beliebigen Form wird durch die DP explizit verboten. Ein passender Gedanke aus der DP heraus ist, dass die Raumzeit und der Äther identisch sind. Eine Raumzeit in der DP verliert gegenüber dem Äther eine entscheidende Eigenschaft, die Raumzeit kann niemals als Referenz für einen Ruhepunkt dienen. Aber genau dafür wurde der Äther gebaut. Das müssen wir auch deshalb genauer betrachten, da die Mathematik zu einem Äther in das Relativitätsprinzip nach Einstein eingeflossen ist.
Die Existenz der Lichtgeschwindigkeit als eine maximale Geschwindigkeit haben wir schon im vorhergehenden Kapitel gezeigt. Das ist aber nicht ausreichend. Das Postulat der Lichtgeschwindigkeit hat zwei Eigenschaften. Es muss zusätzlich gezeigt werden, warum diese Grenze lokal für jeden Beobachter identisch ist. Wenn es ein kleiner und größer gibt, dann können wir doch feststellen, wer näher an der Raumzeitgrenze dran ist, oder? Nein, können wir nicht. Dies hat nichts damit zu tun, dass die Lichtgeschwindigkeit für alle Beobachter identisch definiert ist. Hier geht es wieder einmal darum, dass alle Verformungen der Raumzeit eine lokale Veränderung der Definition der Geometrie sind.
Entgegen den bisherigen Erklärungen müssen wir hier bei Adam und Eva anfangen. Wir gehen hier den klassischen Weg. Wir fangen bei Galileo an und gehen über Newton, Maxwell und Lorentz zu Einstein weiter. Dann werden wir feststellen, dass Einstein mit der Kombination von Lichtgeschwindigkeit und Relativitätsprinzip zwar alles richtig gemacht hat, sich aber auch einen großen Spaß erlaubt hat. Dies wird oft nicht erkannt. Ist für uns aber essenziell. Daher werden wir die Abfolge der Entwicklung ausführlicher betrachten. Mir ist klar, dass dieser Abschnitt für „Eingeweihte“ etwas zäh werden kann. Bitte trotzdem lesen. Ich bin gespannt, ob Euch diese Erkenntnis so bekannt war. Die meisten übersehen dies und stürzen sich gleich auf die Rechnungen. Dann habt Ihr aber den spaßigen Teil der SRT nicht entdeckt.
Galileo wird oft als der Urvater der modernen Physik angesehen. Für uns hat Galileo eines der wichtigsten Gedankenexperimente in die Physik mit eingebracht, die abgeschlossene Kiste. Die brauchen wir bei der SRT ohne und in der ART mit Wechselwirkung. Das war die Grundidee von Galileo zum Relativitätsprinzip. Die abgeschlossene Kiste war bei Ihm eine Schiffskabine, ohne eine Möglichkeit nach außen zu sehen. Das Ganze auf einem sehr ruhig fließenden Wasser. Bei Einstein ein Aufzug oder später ein Raumschiff. Jeder ist ein Kind seiner Zeit.
Sitzen wir in so einer Schiffskabine, können wir nicht feststellen, ob wir mit dem Wasser uns bewegen oder stehen. Das ist identisch zu der Frage: Fließen wir mit dem Wasser oder fließt das Wasser unter dem Schiff hindurch. Es fehlt ein Bezugssystem oder Bezugspunkt, um die Bewegung eindeutig feststellen zu können. Daraus wird abgeleitet, dass sich Bewegung generell nur relativ zu einem Bezugspunkt feststellen lässt. Wir erweitern das Gedankenexperiment mit zwei Kisten, die nur einen kleinen Sehschlitz offen haben. Etwas anderes als die Kisten selbst ist nicht zu erkennen.
Wenn wir in einer Kiste sitzen und rausschauen, so können wir die andere Kiste sehen, wie diese mit gleichbleibender Geschwindigkeit an unserer Kiste vorbeizieht. Wenn wir keine Beschleunigung spüren können, dann können wir für uns nicht feststellen, ob wie uns bewegen und der andere in Ruhe ist oder umgekehrt. Es könnten sich beide Kisten mit unterschiedlicher Geschwindigkeit bewegen und niemand ist in Ruhe. Es könnten sich auch beide Kisten gleichschnell in eine Richtung bewegen, dann würden wir zwischen den Kisten keine Bewegung erkennen. Die einzige erkennbare Größe ist der Unterschied in der Bewegung zwischen den beiden Kisten. Wir können nur die relative Bewegung der Kisten zueinander feststellen. Das ergibt das Relativitätsprinzip.
Zu einem Relativitätsprinzip gehört immer eine Transformation. Das ist der Wechsel der Sichtweise von der einen Kiste zur anderen Kiste. Dies wird die Galileo-Transformation genannt. Die Berechnung ist so einfach, dass ein Physikstudent dazu wohl keine Übungsaufgabe erhält. Genau hier liegt das Problem. Das Relativitätsprinzip nach Galileo ist so einfach, dass man sich keine Mühe macht die Grundlagen zu durchdenken. Einfach kurz erklärt und damit ist alles abgehackt und fertig. Wir müssen uns die Mühe machen und das Grundprinzip dahinter erarbeiten.
Die Gretchenfrage ist: Wann erhalten wir ein Relativitätsprinzip? Gehen wir diese Grundsatzfrage an. Der Ansatz kommt aus dem Beispiel mit den Kisten. Ein Relativitätsprinzip ergibt sich nur, wenn wir ausschließlich Differenzen zwischen Objekten (Kisten) feststellen können. Wir erweitern diese Aussage allgemein auf alle Messungen. Das ist nicht nur bei Geschwindigkeiten so. Dies ist ein generelles Problem der Messung. Wir gehen von der Geschwindigkeit weg und machen dies für eine Länge. Dann werden die Beispiele etwas klarer.
Wir können eine Messung machen, wenn wir mindestens 2 Messpunkte haben. Bei einer Länge ist uns dies klar. Mit einem Messpunkt können wir keine Länge feststellen. Aber auch keine Geschwindigkeit oder elektrische Ladung. Der zweite Messpunkt ist uns nur nicht immer gleich klar. Der andere Messpunkt ist oft der Nullpunkt. Dieser kann aber auch ein Maximalwert sein. Es ist egal, ob wir zu einem maximalen oder einen minimalen Wert eine Messung machen. Für die Angabe eines Wertes benötigten wir immer 2 Messpunkte. Eine Messung ist ein Vergleich. Dies waren bei uns gerade noch die zwei Kisten. Dann können wir eine Differenz messen.
Wir wollen einen absoluten Wert angeben. Dies ist ein Wert, der für jeden beliebige Beobachter gleichbleiben muss. Dann brauchen wir einen für alle Beobachter identischen Messpunkt. Intuitiv wird dies von uns immer mit dem Nullpunkt gleichgesetzt. Dies bedeutet, sobald wir einen für alle Beobachter allgemeinen Referenzpunkt für die Messung festlegen können, ist ein Relativitätsprinzip nicht mehr möglich.
Innerhalb eines Relativitätsprinzips dürfen wir uns bei dem Messwert einer Differenz einig sein. Das nennen wir eine invariante Größe. Die Messpunkte, die zu dieser invarianten Größe geführt haben dürfen dann aber selbst nicht „invariant“ sein. Die Messpunkte müssen sich dann verschieben. Diese müssen explizit unterschiedlich sein, sonst erhalten wir kein Relativitätsprinzip.
Die Grundsatzfrage nun anders formuliert: Wann können wir nur eine Differenz feststellen? Salopp ausgedrückt, wenn uns der Nullpunkt flöten gegangen ist. Es ist uns dann nicht möglich einen Absolutwert anzugeben. Wir kennen keinen allgemeingültigen Referenzpunkt mehr. Dann ergibt sich zwingend ein Relativitätsprinzip. Die einzigen Angaben sind nur noch Differenzen. Daraus folgt, dass diese Sichtweise zwischen den Objekten immer symmetrisch sein muss. Bei einer Differenz muss es egal sein, von welchen Objekt ab wir die Messung starten
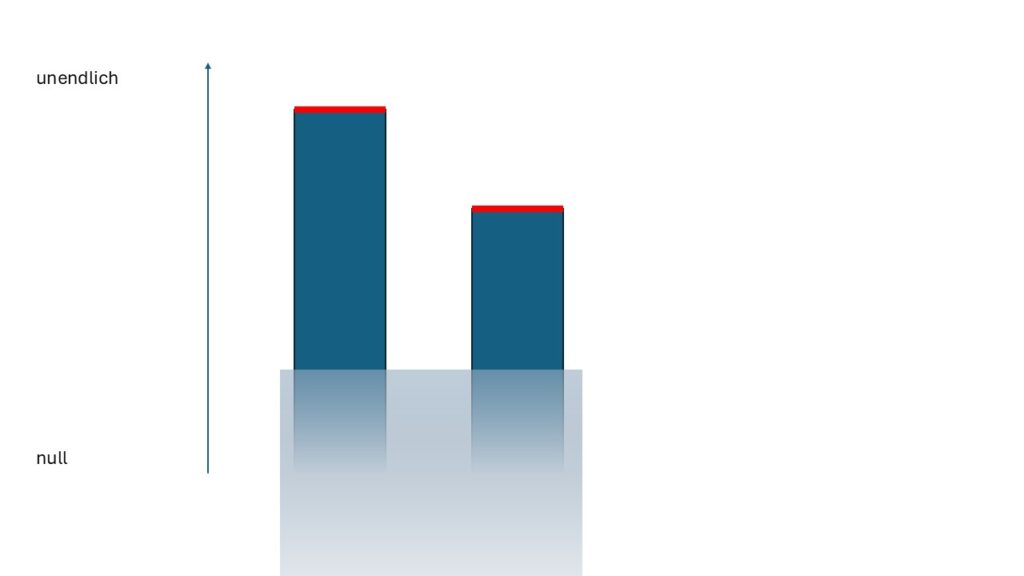
Wir haben zwei Längen. Wir können die absoluten Werte der Längen nicht feststellen. Der Nullpunkt, der für alle Beobachter gültiger Referenzpunkt, ist nicht erkennbar Das einzige erkennbare sind die zwei roten Kanten. Wir erhalten eine Differenz. Damit wir der Differenz einen Wert zuweisen können, legen wir den Nullpunkt einfach auf einer der roten Kanten. Bei einer Geschwindigkeit legen wir eine Geschwindigkeit einfach als null fest. Wir können rein aus der Mathematik heraus den Nullpunkt beliebig setzen. Den „echten“ Nullpunkt kennen wir nicht. Intuitiv wählen wir eine der Kanten aus. Wir erhalten eine symmetrische und relative Messung der beiden Objekte zueinander. Einen absoluten Wert können wir nicht erhalten. Bis hier sollte alles klar sein.
Für einen absoluten Wert könnte wir auch einen maximalen Wert angeben. Der ist genauso gut wie ein null Wert. Bei einer Länge haben wir noch keinen maximalen Wert entdeckt. Zu den Zeiten von Galileo galt dies auch nicht für eine Geschwindigkeit. Warum soll es eine maximale Geschwindigkeit geben? Dafür gab es keinen Grund. Damit war es ausreichend, den Nullpunkt rauszunehmen. Hier kommt der Trick, den wir uns merken müssen. Für Galileo gab es einen Nullpunkt, die absolute Ruhe. Wir können aber diesen Nullpunkt von einer geraden und gleichförmigen Bewegung nicht unterscheiden. Damit ist der Nullpunkt beliebig je Beobachter zu setzen. Dann setzt man sich selbst als den Nullpunkt fest.
Wichtig: Bei Galileo gibt es dann auch kein Größer oder Kleiner für die Werte. Bei einer Differenz kann es auch eine Differenz zwischen einem langen und einem kurzen Stab sein. Um die Länge eines Stabes zu Messen, brauchen wir aber einen Nullpunkt. Es gibt nur einen einzigen Referenzpunkt für alle absoluten Messungen. Genau der ist aber weg. Daraus folgt, dass es bei Galileo immer nur eine 100% symmetrische Sichtweise zwischen den Objekten gibt.
Das Relativitätsprinzip ist so einfach und logisch klar, dass dies Newton als Grundlage für seine Beschreibung der Physik ebenso benutzt hat. Newton und Galileo waren sich beim Relativitätsprinzip einig. Aufgrund der Definition seiner Axiome erkennen wir die Sichtweise für das Relativitätsprinzip bei Newton am besten. Wir haben bei Newton drei Axiome:
Das komische an den Axiomen ist, dass das zweite Axiom das erste Axiom zu enthalten scheint. Wenn wir keine Beschleunigung ausüben, dann gibt es keine Veränderung. Wenn wir keine Veränderung haben, dann bleibt ein Körper kräftefrei und damit in Ruhe oder in einer gradlinigen und gleichmäßigen Bewegung, da es keine Veränderung gibt. Wozu diese Doppelung? Weil es keine Doppelung ist. Das erste Axiom ist die kürzeste und schönste Beschreibung für die Grundlage eines Relativitätsprinzips. Zumindest so, wie man es bis zu Einstein verstanden hat. Wenn man so will, hat Newton das Relativitätsprinzip als Postulat mit aufgenommen.
Newton hat dies nicht wie in den heutigen Lehrbüchern zur SRT gemacht: Postulat, es gilt das Relativitätsprinzip. Das entscheidende an der Aussage von Newton ist für uns, dass ein kräftefreier Körper sich in Ruhe oder in einer geradlinigen und gleichförmigen Bewegung befinden kann. Das lässt sich nicht unterscheiden. Er hat den Grund für das Relativitätsprinzip angegeben. Der allgemeine Referenzpunkt für eine Geschwindigkeit, der Nullpunkt ist nicht mehr gültig. Newton zählt den Zustand der Ruhe explizit mit auf. Er ging, wie Galileo davon aus, dass dieser existiert, aber nicht erkennbar ist.
Die Welt war nach Newton für ca. 200 Jahre in Ordnung. Bis James Clerk Maxwell gekommen ist. Dieser hat eine ähnliche große Leistung wie Newton vollbracht. Newton hat alle einzelnen losen Ideen zur klassischen Mechanik in einer einzigen nahezu vollständig konsistenten Theorie zusammengeführt. Maxwell hat dies mit den einzelnen Teilen der Beschreibung von Elektrizität und Magnetismus gemacht und mit der Elektrodynamik auch eine vollständige konsistente Theorie abgeliefert.
Dadurch ist aber ein uns bekanntes Problem aufgekommen. Die beiden großen Theorien, welche die gesamte Physik zur damaligen Zeit beschreiben sollten, haben an einigen Stellen nicht zusammengepasst. Irgendwie wiederholen sich im Laufe der Zeit die Probleme immer wieder.
Wir greifen uns zwei wichtigen Punkte heraus.
c\space =\space \sqrt{\cfrac{1}{\epsilon_0\space *\space \mu_0}}
Das Problem bei der Beschreibung ist, dass \epsilon_0 die elektrische Feldkonstante und \mu_0[/katex die magnetische Feldkonstante jeweils unveränderliche Naturkonstanten sind. Dies unabhängig vom Bewegungszustand. Dann muss auch c zwingend eine unveränderliche Naturkonstante sein. Die Lichtgeschwindigkeit muss immer gleich sein, egal aus welchem Bezugssystem. Alle Naturkonstanten müssen in jedem Bezugssystem identisch sein. Diese Bezugssysteme sind Inertialsysteme. Damit durften diese sich gleichmäßig und geradlinig Bewegen. Wie soll die Lichtgeschwindigkeit gleichbleiben, wenn man diese aus einem beliebigen Inertialsystem heraus beobachtet?
Zu dieser Zeit war Newton der Halbgott der Physik. Daher hatte man eine Lösung gesucht, die unbedingt mit der Beschreibung von Newton übereinstimmen musste. Das Problem wurde selbst von Maxwell so aufgefasst, dass es in der Elektrodynamik wohl noch etwas unbekanntes geben muss, damit das Relativitätsprinzip auch für die Lichtgeschwindigkeit wieder funktioniert. Wir haben zwar keinen neuen Nullpunkt erhalten, aber einen absoluten maximalen Wert. Das ist ein eindeutiger Referenzpunkt für jeden Beobachter. Damit funktioniert kein Relativitätsprinzip mehr.
Ein Lösungsansatz war der Äther. Man vermutete bereits, dass diese maximale Geschwindigkeit zu dem Licht gehört und das Licht damit eine elektromagnetische Welle ist. Also musste diese Wellenbeschreibung des Lichtes ein Medium besitzen. Wie die Welle im Wasser oder der Schall in der Luft. Dieses Medium zur Ausbreitung und Anregung der elektromagnetischen Welle soll der Äther sein. Dann hat die Lichtgeschwindigkeit nur zum Äther diesen absoluten Wert der Geschwindigkeit. Das Relativitätsprinzip nach Galileo wäre damit gerettet und nur in Bezug auf den Äther nicht richtig. Der Äther musste dann gleich der absolute Nullpunkt, also Ruhepunkt, für die Lichtgeschwindigkeit sein. Zum Äther musste diese immer einen absoluten Wert aufweisen, aber nicht zum Raum des Beobachters (Raumzeit gab es noch nicht).
Es wurde bereits früh erkannt, dass diese Äther sehr seltsame Eigenschaften haben muss, damit dies alles funktioniert. Zusätzlich konnte dieser Äther in keinem Experiment nachgewiesen werden. Insbesondere das Experiment von Michelson und Morley aus dem Jahre 1881 und 1887 hat einer Äther-Theorie große Probleme bereitet. Dort sollte ein Äther über die Bewegung der Erde durch den Äther gefunden werden. Das Ergebnis war negativ und ist es bis heute geblieben.
Die Rettung des Äthers, nur für dieses Experiment, denn die anderen Probleme sind geblieben, ist dann von Hendrik Antoon Lorentz gekommen. Es wurde eine neue Transformation entwickelt, die Lorentz-Transformation. Diese ist so aufgebaut, dass eine Existenz eines Äthers mit dem Michelson-Morley-Experiment verträglich ist. Dafür musste aber in Bewegungsrichtung eine Länge kürzer und die Zeit langsamer werden. Längenkontraktion und Zeitdilatation waren schon vor der SRT bekannt. Für Lorentz war die Längenkontraktion nur im elektromagnetischen Feld (Äther) vorhanden und die Zeitdilatation ein reines mathematisches Hilfsmittel.
Rein mathematisch hatte Lorentz eine Lösung gefunden. Jetzt kommt der Witz an der Sache. Diese ist für eine Äther-Theorie entwickelt worden. Damit funktioniert die Lorentz-Transformation nur mit einem absoluten Nullpunkt und der dazugehörenden absoluten Geschwindigkeit. Das sollte klar sein. Wenn eine absolute Geschwindigkeit angenommen wird, dann muss es dazu einen absoluten Referenzpunkt geben. Hier war es der Nullpunkt in Bezug auf einen Äther.
Jetzt aber endlich zu unserem Spaßvogel. Die SRT hat aus meiner Sicht tatsächlich mehrere Väter. Es gab dazu schon etliche andere Entwicklungen von mehreren Personen um diesen Themenbereich. Einstein hat hier die letzte zündende Idee mit eingebracht. Er hat zur Entwicklung der SRT, wieder nur aus meiner Sicht, folgende Annahmen getroffen:
Diese Punkte sind ausreichend, um auf die SRT zu kommen. Wir können damit folgende Logik aufbauen:
Damit erhält man fast die SRT. Für eine saubere Begründung der Längenkontraktion und Zeitdilatation der Raumzeit, was zu Einsteins Zeit eine sehr mutige Annahme war, hat Einstein viel mit der Gleichzeitigkeit in der Raumzeit argumentiert. Besser ausgedrückt, mit der nicht mehr vorhandenen Gleichzeitigkeit. Dafür musste er eine zusätzliche Annahme machen, welche vorher nicht gegeben war. Die Lichtgeschwindigkeit ist nicht nur konstant, sondern auch noch maximal. Laut Maxwell ist c einfach nur konstant für elektromagnetische Wellen. Für Einstein musste diese nun maximal für jegliche Wirkung in der Raumzeit sein. Nur mit dieser Erweiterung ergibt sich eine SRT. Daher sieht diese Bedingung für viele wie ein „Fremdkörper“ in der Theorie aus.
Durch die maximale Geschwindigkeit kann es für eine Wirkung von einem Raumzeitpunkt zu einem anderen Raumzeitpunkt keine Gleichzeitigkeit mehr geben. Die Wirkung benötigt immer Zeit zwischen den Raumzeitpunkten. Wir werden gleich eine andere Vorgehensweise aufbauen, die zur DP besser passt und die Diskussion mit der Gleichzeitigkeit für Längenkontraktion und Zeitdilatation umgeht.
Wenn wir dieser Logik folgen, dann erkennen wir, nach meiner Meinung, den Witz an der Sache nicht. Gleiches gilt für die Argumentation mit der Gleichzeitigkeit, welche wir hier nicht weiterverfolgen werden. Genau so wird es aber in den Lehrbüchern erklärt. Daher fällt es fast keinen auf. Einstein hat nicht einfach das alte Relativitätsprinzip von Galileo verändert. Er hat ein komplett anderes Relativitätsprinzip aufgebaut. Die Grundannahmen der Galileo-Transformation und der Lorentz-Transformation schließen sich gegenseitig aus, wenn wir keinen Äther mehr haben.
Was hat Einstein den getan, dass ich Ihn für so einen Spaßvogel halte? Seine zwei Prinzipen sind:
Die beiden Prinzipien schließen sich gegenseitig aus. Das ist es, was ich meinte, dass sich die Galileo- und die Lorenz-Transformation bereits in den Grundannahmen nicht vertragen.
Kein Problem, dann hat eben Einstein Recht und Galileo nicht. Leider geht dies in der DP nicht so einfach. Wir werden als Argumentation für ein Relativitätsprinzip ein drittes Konzept aufbauen. Dieses folgt eher der Annahmen von Galileo und Newton. Zusätzlich muss aber Einstein auch Recht haben, obwohl sich die Ansätze gegenseitig ausschließen. Die SRT ist seit 120 Jahre in allen Berechnungen zu den Experimenten ohne Fehl und Tadel. Diese kann nicht falsch sein. Die unterschiedlichen Ansätze zur Relativität müssen unter bestimmten Umständen mathematisch identisch sein. Das Kunststück gelingt nur dadurch, dass alle Verformungen der Raumzeit eine Veränderung der Definition der Raumzeitgeometrie sind.
Daraus ergibt sich sofort die neue Gretchenfrage: Wieso funktioniert die SRT überhaupt? Das ergibt doch niemals ein Relativitätsprinzip. Doch tut es, nur nicht so wie sich dies alle vorstellen. In den beiden Relativitätstheorien werden grundsätzlich unterschiedliche Dinge miteinander verglichen. Darauf kommen wir nur, wenn wir uns die Grundlagen ansehen. Die Argumentationskette in den Lehrbüchern ist immer erst Galileo und dann dieses Relativitätsprinzip, durch Einstein abgeändert, zur SRT. Hier bin ich mir auch nicht sicher, ob dieser Unterschied von Einstein selbst erkannt wurde. Durch dieses Vorgehen übertragen wir einfach die Idee des Relativitätsprinzips von Galileo auf die SRT. Die SRT ist die Spezielle Relativitätstheorie. Klingt so, als sei dies nur ein Spezialfall der Relativität. Dieses Vorgehen ist falsch. Um dies zu klären, müssen wir was tun? Genau die nächste Grundsatzfrage stellen.
Was für Objekte werden, im Relativitätsprinzip nach Galileo verglichen? Erstmal unsere zwei Kisten. Die Kisten in Bezug auf was? Nur auf sich selbst, da uns der Referenzpunkt abhandengekommen ist. Der Referenzpunkt in Bezug auf was? Den umliegenden Raum. Wir dürfen bei Galileo und Newton nur von Raum sprechen. Eine Raumzeit mit dynamischer Längen- und Zeitdefinition war hier noch nicht bekannt. Das heißt ganz allgemein, wir vergleichen die Bewegungszustände verschiedener Objekte im identischen Raum. Diese niemals hinterfragte Grundstruktur wird nun in die SRT übertragen. Wie wir aus den Prinzipen gelernt haben, kann die SRT dies nicht tun. Die SRT muss etwas anderes machen.
Ich erspare euch die nächste Fragerunde und bringe gleich die Auflösung. Die SRT ist immer noch ein Relativitätsprinzip. Damit muss diese Objekte vergleichen. Es sind aber nicht unsere Kisten in einer Raumzeit. Die SRT vergleicht zwei fixe Raumzeiten, welche jeweils einer Kiste zugeordnet sind. In der SRT vergleichen wir nicht zwei Objekt in einer dynamischen Raumzeit. Wir vergleich zwei statische Raumzeiten die wir je Objekt zuweisen. Ein vergleich ja, aber eigentlich nicht der Vergleich den wir wollen.
Dazu ein kleiner Einschub, aus meinem persönlichen Erlebnis heraus. Als ich mir diese Grundlagen erarbeitete, diskutiert ich natürlich mit anderen darüber. Mal in einem persönlichen Gespräch oder in einem Physikforum. Dabei habe ich von unterschiedlichen Personen folgende Interpretation der SRT erhalten:
Das entscheidende daran ist, hätte ich diese Personen in einen Raum gesteckt und Ihnen eine rein mathematische Aufgabe zur SRT gegeben, dann bin ich mir zu 100% sicher, dass alle diese Personen zu dem identischen und absolut korrekten Ergebnis gekommen wären. Die Personen hätten sich gegenseitig gratuliert und behauptet wir haben alles identisch verstanden, da wir es richtig berechnen können. Das ist der Unterschied von Berechnen und Erklären.
Können wir zwischen Raumzeiten ein Relativitätsprinzip erzeugen? Schauen wir uns doch mal einen Vergleich laut SRT an.
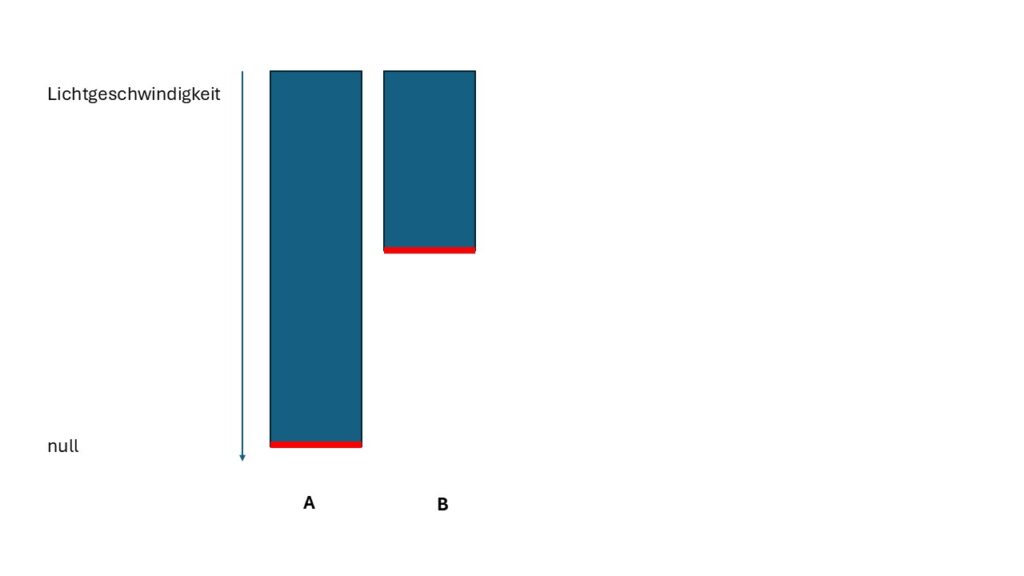
Hier sehen wir wieder zwei Längen. Dabei starten beiden vom Nullpunkt ab mit einer jeweils unterschiedlichen Länge zueinander. Beide Längen starten vom Nullpunkt in ihrer Raumzeit. Dann brauchen wir noch den Endpunkt, die Lichtgeschwindigkeit. Die muss für alle identisch sein. Sonst ist ein Vergleich bei verschiedenen Geometrien nicht möglich. Genau hier liegt ein entscheidender Punkt in der SRT. Wenn wir eine dynamische Geometrie haben, dann brauchen wir mindestens einen absoluten Referenzpunkt, damit wir die Geometrien überhaupt vergleichen können. Das übernimmt die Lichtgeschwindigkeit. Die Lichtgeschwindigkeit, als absoluter Referenzpunkt, „versaut“ uns die Relativität nicht, wir brauchen diese zwingend. Den Nullpunkt in jeder Geometrie brauchen wir, damit wir eine einheitliche zweite „Kante“ zur Differenzmessung erhalten. Daher funktioniert die Lorentz-Transformation mit den absoluten Werten für den Ruhepunkt und der Lichtgeschwindigkeit. Wir benötigen diese Punkte zwingend, damit wir eine Raumzeitgeometrie überhaupt vergleichen können.
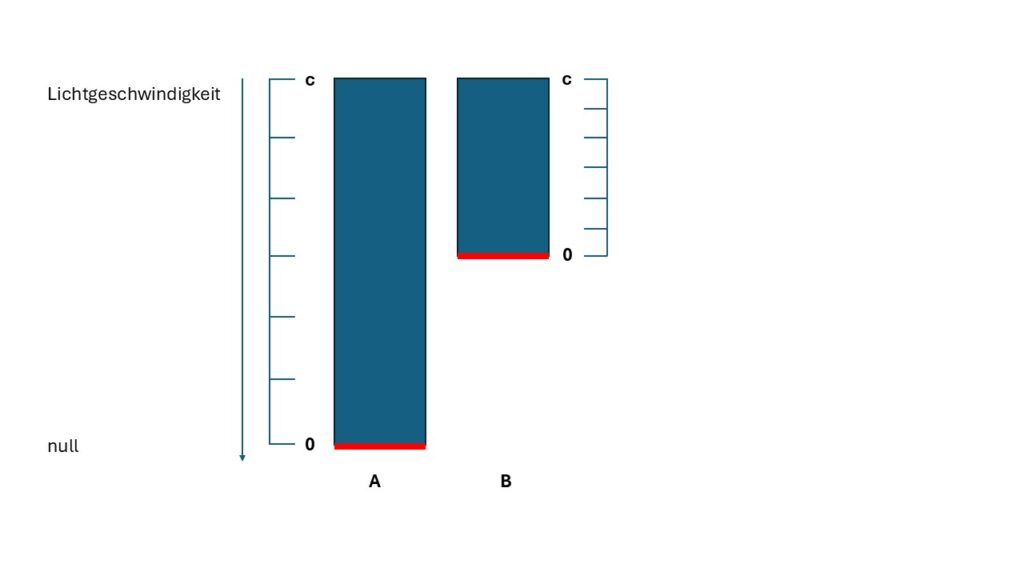
Dafür muss bei B eine andere Längeneinteilung gewählt werden. Die Menge an Einteilungen muss in beiden Fällen gleich sein. Von Null zu Lichtgeschwindigkeit soll für alle der identische Absolutwert sein. Dieser Vergleich ist wieder symmetrisch. Wir könnten bei A und bei B das Ruhesystem setzen. Damit kann A und B jeweils eine absolute Wertangabe in der Raumzeit A und B sein. Das ist kein Problem. In der jeweiligen Raumzeit wird kein Vergleich gemacht. Die Raumzeiten A und B werden verglichen. Wir sehen, das Relativitätsprinzip funktioniert auch zwischen unterschiedlich definierten Raumzeiten.
Dann muss unserer Bedingung, keine Referenzpunkt, für die Raumzeiten selbst und nicht nur für ein Objekt in der Raumzeit funktionieren. Die Raumzeiten zueinander dürfen keinen absoluten Referenzwert besitzen. Dazu schauen wir uns den Aufbau eines normales Raumzeitdiagramms an.
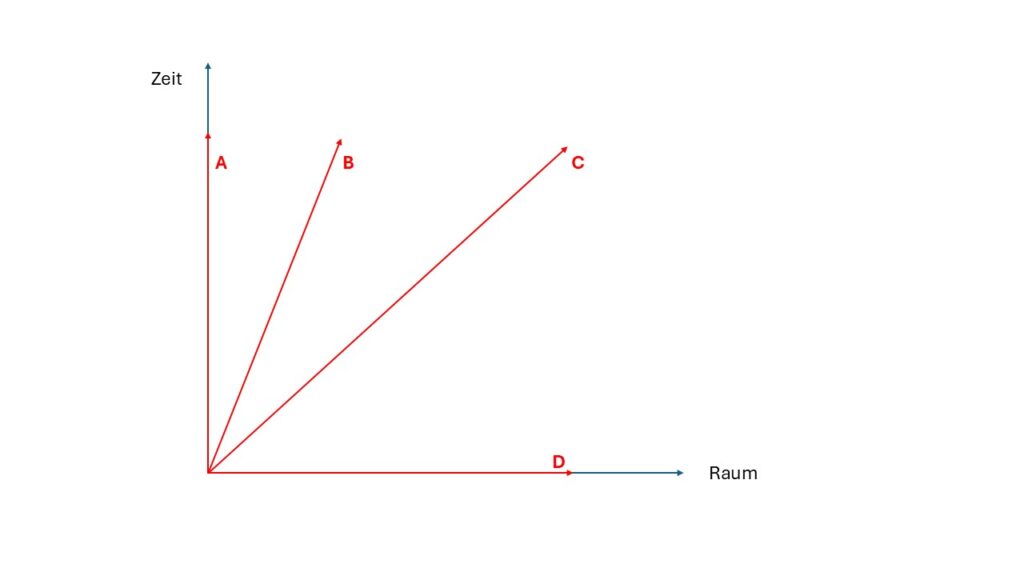
Schauen wir uns die gegebenen Möglichkeiten an:
In allen Fällen bewegen wir uns, wenn auch einmal nur in der Zeit oder nur im Raum. Was es explizit für eine Raumzeit nicht gibt, ist Ruhe. Selbst wenn kein Objekt in der Raumzeit vorhanden ist und nur die Raumzeit selbst vorhanden wäre, so vergeht die Zeit. Das ist in der Mathematik der SRT auch eine Bewegung. Eine Raumzeit als eigenständiges Objekt kennt keinen Zustand der Ruhe. Uns ist, zum Glück, wieder die Null flöten gegangen. Innerhalb der Raumzeit setzen wir einfach einen Ruhepunkt und erzeugen absolute Werte. Für die Raumzeit selbst ist dies nicht möglich.
Was ist aber mit einer maximalen Geschwindigkeit. Wir haben doch die Lichtgeschwindigkeit. Ja, der wird aber nun zwingend benötigt, damit ein Vergleich überhaupt möglich ist. Wenn beide Raumzeiten unterschiedliche Geometrien aufweisen, muss es für einen Vergleich einen gemeinsamen Referenzpunkt geben. Wir könnten sonst nicht einmal eine Differenz angeben.
Für Raumzeiten können wir nur einen Referenzpunkte, die Lichtgeschwindigkeit festlegen und diese brauchen wir dringend, damit wir überhaupt einen Vergleich machen können. Wir erhalten ein waschechtes Relativitätsprinzip zwischen Raumzeiten, aufgrund von veränderlicher Geometrie in den Raumzeiten. Das ist die SRT. Damit können wir gleich mehrere Probleme lösen. Wir können damit erklären, warum das Zwillings-Paradoxon für die SRT so schwierig ist, das machen wir in 4.11. Wir können einen Punkt klären, denn ich Cherry Picking genannt habe, das mache wir in 4.10. Wir können erklären, warum die SRT zur QM besser passt als zur ART, in 4.12. Wir werden erkennen, dass mit dieser Interpretation die SRT erst so richtig Sinn macht.
Es bleibt noch eine Frage aus dem Relativitätsprinzip nach Galileo offen. Kann es in der SRT ein Größer oder Kleiner geben? In der SRT erkennen wir auch nur Differenzen. Jeder der diese Differenzmessung machen will, muss sich zwingend auf den Nullpunkt setzen. Bei Galileo hatten wir nur einen möglichen Referenzpunkt. Der musste weg, sonst erhalten wir kein Relativitätsprinzip. Das ist bei der SRT nicht der Fall. Wir haben einen Nullpunkt und die Lichtgeschwindigkeit. Die brauchen wir aber um die Differenz feststellen zu können. Da kommt im ersten Ansatz kein größer oder kleiner raus. Wenn wir so eine Angabe haben wollen, brauchen wir explizit einen weiteren Referenzpunkt zwischen den Raumzeiten. Wir werden sehen, dass das Zwillingsparadoxon uns diesen liefert und wir deshalb ein Jünger und Älter feststellen können. Das geht auch nur in der Zeit und nicht im Raum. Das werden wir aber im passenden Abschnitt besprechen.
Bevor alle diese Punkte auflösen, müssen wir was anders angehen, dann werden diese Lösungen noch klarer. Wir müssen erstmal die neue Sichtweise über die DP aufbauen. Diese soll das Relativitätsprinzip von Galileo, alles in einer Raumzeit und das Relativitätsprinzip nach Einstein, Vergleich von Raumzeiten zusammenführen. Ob Ihr es glaubt oder nicht, wir kennen bereits alle nötigen Bestandteile dafür.
Wir führen für diese Variante der SRT keinen neuen Namen ein. Die alte Variante nach Galileo und Newton sind einfach das Relativitätsprinzip. Die Variante nach Einstein ist die SRT und wir haben nun erkannt, dass diese tatsächlich sehr spezielle ist. Für unserer neue Variante bleiben wir einfach bei der Bezeichnung SRT. Da die SRT in beiden Varianten mathematisch identisch ist, brauchen wir keine neuen Namen.
Was wollen wir den haben. Wir wollen einen Vergleich von zwei Objekten in einer Raumzeit. Denn das ist es, was wir eigentlich meinen, wenn wir von einem Relativitätsprinzip sprechen (Galileo). Dann müssen wir in einer einzigen Raumzeit mit unterschiedlichen Geometrien der Raumzeit umgehen können, ohne dass dafür ein Absolutwert benutzt werden muss. Wie am Anfang erwähnt, machen wir dies mit unserer Raumzeitdichte. Diese muss alle benötigten Eigenschaften aus beiden Varianten beinhalten. Klingt wieder sehr schwer, ist aber einfach. Das haben wir bereits durch unseren Ansatz mit eingebaut. Wir unterscheiden nicht zwischen Bühne und Akteur. Eine Raumzeitdichte ist immer auch Raumzeit selbst. Damit muss die Eigenschaft nur vorhanden sein, dann ist diese automatisch in beiden Varianten da. Wir können die Varianten auch anders aufteilen. Bei Galileo werden die Akteure auf einer Bühne verglichen. Bei Einstein werden die Bühnen verglichen. Wir kennen diesen Unterschied nicht mehr.
Was uns jetzt noch das Leben einfach macht, ist das eine Raumzeitdichte immer Energie, Geometrie und Bewegungszustand in einem ist.
Wenn wir zwei Raumzeitdichten vergleichen wollen, darf es keinen Nullpunkt für eine Raumzeitdichte geben. Das haben wir im Kapitel 3 ausführlich behandelt. Eine Raumzeitdichte von null kann es nicht geben. Sonst ist der Raumzeitpunkt nicht in der Raumzeit vorhanden. Damit haben wir für diesen Abschnitt schon alles erledigt. Per Definition kann es für eine Raumzeitdichte keinen Nullpunkt geben. Da der Bewegungszustand selbst Raumzeit ist, kann es keinen Ruhepunkt in einer Raumzeitdichte geben. Entgegen Galileo und Newton können wir den Ruhepunkt nicht einfach nur nicht unterscheiden, wir haben per Definition keinen Ruhepunkt.
Bei einem höheren Impuls haben wir mehr Raumzeitdichte. Diese kann ich doch zur Lichtgeschwindigkeit in Bezug setzten. Für die Raumzeitdichte ist die Grenze unendlich. Damit ist kein Grenzwert vorhanden. Für den Bewegungszustand ergibt sich aber ein absoluter Wert, die Lichtgeschwindigkeit. Damit ist eine Referenzpunkt vorhanden. Es sollte in der DP kein Relativitätsprinzip bei Geschwindigkeiten vorhanden sein. So einfach geben wir uns nicht geschlagen.
Wir haben die Lichtgeschwindigkeit in der Raumzeit. Diese ist durch die Geometrie eindeutig festgelegt und damit ein absoluter Wert. Die Aussage ist richtig. Wir haben trotzdem keinen Referenzpunkt in der Raumzeit. Den haben wir nur zwischen Raumzeiten. Wir machen hier den Trick wie bei Newton mit der Ruhe. Dort hatten wir die Ruhe oder die geradlinige und gleichförmige Bewegung. Da wir beide Zustände nicht unterscheiden können, ist der Nullpunkt weggefallen. Etwas ähnliches passiert uns mit der Lichtgeschwindigkeit. Diese ist für jedes Objekt immer identisch weit weg und kann damit nicht als Referenzpunkt einer Messung innerhalb einer Raumzeit benutzt werden. Das war die Grundidee von Einstein. Dort ist es aber ein Postulat. Dieses dürfen wir so nicht benutzen. Wir müssen diese Konstanz der Lichtgeschwindigkeit herleiten. Das machen wir im nächsten Abschnitt.
Die Existenz der Lichtgeschwindigkeit haben wir in Kapitel 3 ausführlich besprochen. Diese ist als ein Strukturelement der Raumzeit zwingend durch die Raumzeitgrenze gegeben. Damit ist aber nur der erste Schritt erreicht. Wir haben eine identische Bedingung. Diese erzeugt, explizit nicht die Konstanz der Lichtgeschwindigkeit.
Im zweiten Schritt müssen zeigen, dass wie trotz dieser Bedingung einen identischen Abstand zu jedem Objekt haben. Dafür gibt es zwei Möglichkeiten. Eine davon ist falsch. Leider wird die falsche Möglichkeit sehr oft herangezogen. Schauen wir uns die beiden Möglichkeiten genauer an.
Das Thema hatten wir schon bei den Planck-Werten. Die Geschwindigkeit ist ein Bruch \frac{Länge}{Zeit}. Damit gibt es unendlich viele Werte, welche zur identischen Geschwindigkeit führen. In der SRT verändern sich die Längen- und Zeitdimension identisch. Damit ergibt sich für den Bruch insgesamt als Wert keine Veränderung. Die Länge und die Zeit werden im gleichen Maße kleiner und größer. Die Geschwindigkeit verändert sich damit nicht und muss lokal gleichbleiben.
Ein Teil in der Argumentation ist richtig. Wir dürfen keine Veränderung erkennen können. Der zweite Teil, dass dies dadurch passiert, weil die Geschwindigkeit ihren Wert als Bruch nicht verändert ist leider falsch, obwohl es richtig aussieht.
Das beste Gegenbeispiel ist die Shapiro-Verzögerung, da experimentell gut bestätigt. Diese besprechen wir genauer im nächsten Kapitel für das Äquivalenzprinzip der ART. Für uns jetzt wichtig ist, dass sich Licht in einem Gravitationsfeld für einen externen Beobachter auch langsamer bewegen kann. Lokal muss das Licht aber wieder mit c unterwegs sein. Hier verändert sich Länge und Zeit gegenläufig. Das ergibt niemals eine lokal konstante Geschwindigkeit über einen Bruch. Obwohl wir in der SRT sind, brauchen eine allgemeinere Lösung, die auch im Umfeld der Gravitation funktioniert.
Der erste Gedanke war, wir können die Veränderungen erkennen, diese heben sich aber gegenseitig auf. Damit die Konstanz der Lichtgeschwindigkeit funktioniert, dürfen wir eine Veränderung in den Komponenten der Raumzeit lokal erst gar nicht erkennen können. Dann ist es irrelevant, wie das Umfeld aussieht oder sich die Raumzeitkomponenten gegenseitig verhalten. Dies erreichen wir dadurch, dass die Raumzeitdichte durch die Definition der Geometrie bestimmt wird. Da alles im Universum eine Raumzeitdichte ist, ist auch die lokale Konstanz von jeder beliebigen Größe erreicht.
Fangen wir mit der Länge an. Die Veränderung der Raumkomponente kann ausfallen, wie sie will, wir können diese lokal niemals erkennen. Der Meter als Referenzgröße wird nicht gequetscht. Er ist lokal für das Objekt anders definiert. Fliegt ein Raumschiff mit ca. 86% der Lichtgeschwindigkeit, dann ist der Meter für uns in Bewegungsrichtung nur noch halb so lang. Im Raumschiff gibt es jedoch physikalisch keine Möglichkeit dies festzustellen. Absolut alles im Raumschiff hat nun die neue Längendefinition. Ein Meter bleibt lokal immer ein Meter. Wir können bereits lokal die Veränderung nicht erkennen.
Die Zeit verhält sich identisch zur Länge. Die Sekunde ist nun anders definiert. Es gibt keine Möglichkeit dies festzustellen. Aber wir haben doch die Zeit als Abstandsmaß zur Raumzeitgrenze festgelegt. Das Raumschiff ist der Raumzeitgrenze nähergekommen. Ja, das ist richtig. Lokal können wir auch das nicht feststellen. Wir müssten eine Längenkontraktion oder eine Zeitdilatation feststellen können, um dies bestimmen zu können. Diese Möglichkeit fehlt uns. Aus Sicht des Raumschiffes ist es der Raumzeitgrenze kein bisschen entgegengekommen. Daher bleibt lokal alles wie es ist.
Lokal ist es nicht möglich eine Veränderung feststellen zu können
Lokal ist keine Annäherung an die Raumzeitgrenze erkennbar. Diese muss immer identisch weit entfernt bleiben. Konstanz der Lichtgeschwindigkeit.
Dieses „lokal keine Veränderung erkennbar“ hat nicht nur die Konstanz der Lichtgeschwindigkeit im Gepäck. Dies erklärt auch, warum wir laut SRT alles in ein Ruhesystem setzen können. Der Abstand zur Raumzeitgrenze verändert sich lokal nicht und ein Nullpunkt gibt es nicht. Damit kann sich jedes Objekt ohne Beschleunigung als in Ruhe betrachten. Wenn sich die Definition von Länge und Zeit nicht ändert, dann haben wir immer ein Initialsystem. Jeder lokale Beobachter hat eine gute Definition von Länge und Zeit. Diese dürfen lokal von Beobachter zu Beobachter anders ausfallen, lokal ist aber je Beobachter eine eindeutige Definition und damit ein Inertialsystem vorhanden. Dies ist der Grund, warum wir überhaupt erst mit der Idee eines Inertialsystems arbeiten dürfen. Das ist die Verbindung von SRT, Vergleich der Raumzeiten, zu altem Relativitätsprinzip, Vergleich von Objekten in einer Raumzeit.
Schauen wir uns das Relativitätsprinzip in der DP anhand eines Beispiels an. Wir machen hier den Klassiker und nehmen eine Person auf der Erde und eine in einem Raumschiff, welches sich von der Erde entfernt.
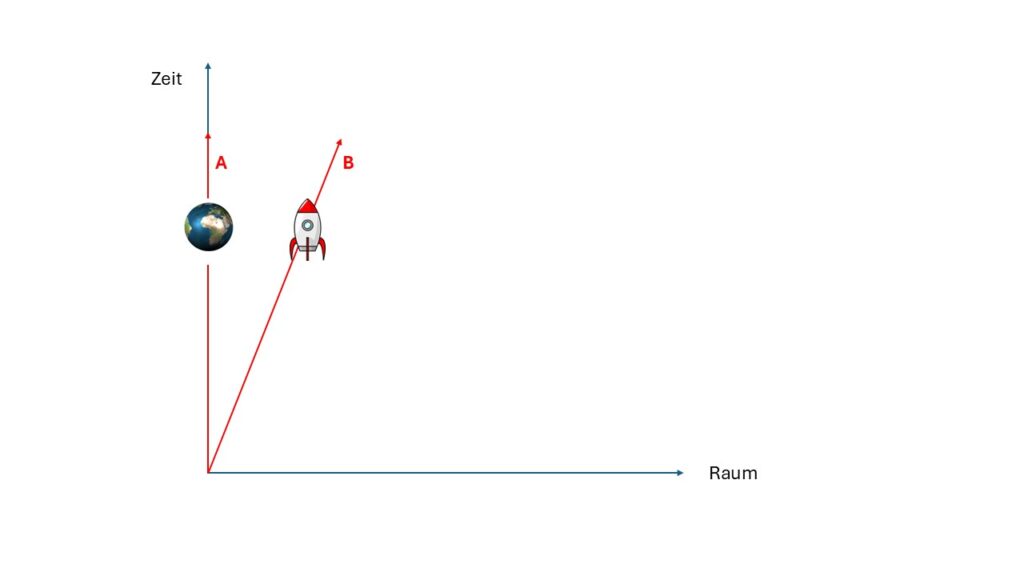
Dann haben wir zwei Sichten zu besprechen. Einmal von der Erde und einmal vom Raumschiff aus. Wir beginnen mit dem einfachen Fall.
Hier sind sich SRT und DP in der Sichtweise einig. Daher ist der Fall einfach. Die Person auf der Erde erfährt keine Veränderung des Bewegungszustandes. Damit bleibt die Raumzeitdichte identisch. Für die SRT bleibt diese Person einfach im Ruhesystem. Das Raumschiff wird beschleunigt und bekommt damit tatsächlich eine höhere Raumzeitdichte. Das Raumschiff erfährt eine Längenkontraktion und eine Zeitdilatation. Dies kann real von der Erde aus gemessen werden. Im Raumschiff kann davon aber nichts erkannt werden, soweit herrscht Einigkeit.
Längenkontraktion und Zeitdilatation sind eine echte physikalische Veränderung des Raumschiffes. Nicht nur eine Sichtweise. Genau diese Aussage führt zur Vermutung, dass die Raumzeitdichte keinem Relativitätsprinzip unterliegt.
Bei der SRT scheint alles erstmal sehr einfach zu sein. Wenn das Raumschiff seine Beschleunigungsphase hinter sich hat, kann es von sich behaupten, es ist in Ruhe. Die Erde hat sich beschleunigt und fliegt vom Raumschiff weg. Die Erde muss nun zwingend einer Längenkontraktion und einer Zeitdilatation unterliegen. Eine vollkommen symmetrische Sicht.
Genau hier fangen im Verständnis zur SRT, die Probleme an. Die Beschleunigungsphase ist nur und ausschließlich am Raumschiff erfolgt. Wieso soll nun die Erde anders sein als vorher. Die Erde reicht in dieser Betrachtung gar nicht aus. In Bewegungsrichtung muss sich das gesamte Universum beschleunigt haben. Nein, ganz bestimmt nicht. Das Universum verändert sich nicht, nur weil irgendwo ein Raumschiff eine Beschleunigungsphase gehabt hatte. Daran erkennen wir am besten, dass die SRT nicht zwei Objekte (Erde und Raumschiff) in einer Raumzeit vergleicht. Je nach Sichtweise, werden den Objekte eine passende Raumzeit, welche immer von null bis Lichtgeschwindigkeit geht, zugewiesen. Dann wird der Vergleich der Raumzeiten gemacht. Daher muss aus Sicht des Raumschiffes das gesamte Universum eine Veränderung erfahren haben. Nur das Raumschiff hatte eine Beschleunigungsphase und hat diese neue Definition der Raumzeit bekommen. Es ist aber eine Definition einer kompletten Raumzeit.
Die SRT kennt beim Vergleich allerdings nur eine Richtung. Das andere Objekt hat immer die „kleinere“ Definition mit Zeitdilatation und Längenkontraktion. Bei einem Relativitätsprinzip sollte es nur eine Differenz geben und keine bestimmte Richtung. Das ergibt sich wiederum zwanghaft aus dem Ansatz mit der Lorentz-Transformation aus einer Äthertheorie heraus. Diese geht von einem im gesamten Universum identischen Nullpunkt aus. Daher erhalten wir in der SRT diese Vorzugsrichtung im Vergleich.
In der DP darf nur das Raumschiff die höhere Raumzeitdichte haben. Nur dort ist eine Beschleunigung aufgetreten. Dann hat das Raumschiff eine veränderte Definition der Geometrie. Das Raumschiff erkennt genauso wie die Erde, dass ein Unterschied in der Definition der Geometrie vorliegt. Nur dieser Unterschied wird erkannt. Selbst wenn für das Raumschiff klar ist, welcher derjenige mit der höheren Raumzeitdichte sein muss, können wir dies nicht aus dem Raumschiff heraus messen. Im Raumschiff ist nun eine andere Definition der Geometrie vorhanden. Das Raumschiff darf nun alle Beobachtungen nach außen nur noch mit seiner Definition erkennen. Gehen wir streng nach SRT vor. Dann ist das Raumschiff in Ruhe und die Erde hat beschleunigt. Wie sieht es für das Raumschiff nach der DP aus. Die Erde hat ihre Geschwindigkeit definitiv beibehalten. Damit aber auch ihre Raumzeitdefinition. Der Meter der Erde ist länger definiert als der Meter im Raumschiff. Dann schafft die Erde, aus Sicht des Raumschiffes, mehr Länge bei gleichbleibender Geschwindigkeit. Damit muss sich für das Raumschiff die Erde beschleunigt haben. Nicht nur die Erde, das gesamte verdammte Universum. Nur das Raumschiff hat seine Raumzeitdichte verändert. Damit muss für das Raumschiff zwingend das gesamte Universum einer Veränderung unterliegen.
Die DP macht eine Raumzeitveränderung nur an dem Objekt, dass auch eine Beschleunigungsphase gehabt hat. Dann ergibt sich aber eine globale Veränderung für das Objekt. Die SRT macht dies dadurch, dass es jedem Objekt immer eine komplette Raumzeit zuweist. Dann scheinen die Sichtweisen DP und SRT identisch zu sein. Warum dann der ganze Aufstand? Weil diese nicht identisch sind.
In der DP hat das Raumschiff tatsächlich eine höhere Raumzeitdichte. In der SRT können wir dies so nicht bestimmten. Da geht immer nur ein symmetrischer Ansatz. In der DP ist klar, dass Längenkontraktion und Zeitdilatation nur lokale Phänomene sind. In der SRT sind diese immer Global je Sichtweise. Diese beiden Punkte klären wir in den nächsten zwei Abschnitten.
Laut der SRT tritt die Zeitdilatation und die Längenkontraktion immer identisch und physikalisch messbar in der gesamten Raumzeit auf. Dann bekommen wir aber ein logisches Problem. Mathematisch ist alles sauber, da symmetrisch. Logisch wird es hier kritisch. Der Ansatz aus der DP löst dieses Problem sehr einfach.
Ich habe dieses Problem, wie immer, kraft souveräner Willkür „Cherry Picking“ genannt. Wenn ich in meinen Stuhl sitze und den Text schreibe, dann habe ich vor mir zwischen meinen zwei Händen eine definierte Zeit und eine definierte Länge. Nun kommen kontinuierlich von allen Seiten der Erdatmosphäre Myonen auf diese Länge zu. Da Myonen sehr schnell sind, muss für diese Teilchen die Länge, je nach Winkel zu meinen Händen, unterschiedlich sein. Das können wir uns nicht wirklich vorstellen.
Da machen fast alle Diskussionspartner eine recht eigenwillige Unterscheidung. Jedes Myon muss eine andere Zeit haben als meine. Das sind von meinen Händen unterschiedliche Objekte. Diese können unterschiedliche Zeitverläufe haben. Da Zeit ein Mysterium bleibt, wird dies einfach akzeptiert. Das ist auch gut so, da man die Zeitdilatation per Experiment inzwischen mit beindruckender Genauigkeit überprüft hat. Hacken dran.
Laut der SRT muss sich aber auch zwingend die Länge physikalisch verändern. Zeitdilatation gibt es nur mit Längenkontraktion. Zeitdilatation wird experimentell gemessen, dann muss im Umkehrschluss auch die Längenkontraktion physikalisch auftreten. Damit muss der Abstand zwischen meinen Händen ständig ein anderer sein. Je nachdem in welchem Winkel das Myon zu meinen Händen sich bewegt. Das akzeptiert fast niemand. Da verlassen viele den Pfad der Tugend und gehen auf das, was logisch verständlich ist. Die Längenkontraktion ist nur eine Sichtweise, die Zeitdilatation ist real. Das macht aus logischer wie mathematischer Sicht der SRT keinen Sinn. Entweder ist beides nur eine Sichtweise oder beides ist physikalisch messbar. Bei der Zeit sind wir uns sicher, da gemessen. Bei der Länge wollen wir es nicht hinnehmen, „Cherry Picking“ eben. Das Problem entsteht dadurch, dass die SRT immer eine komplette Raumzeit zuweist. Tatsächlich ist dies logisch nicht sinnvoll. Da die Mathematik aber sehr gut funktioniert => shut up and calculate.
In der DP ist es klar. Es ist immer ein echter physikalischer Effekt. Dieser ist aber nur lokal im Objekt. Vom Objekt aus ergibt sich dann die passende Sichtweise auf das restliche, nach der lokalen Definition, unveränderte Universum. Ein Cherry Picking wird nicht benötigt.
Sorry, aber wenn wir die SRT durchkauen, dann darf das Zwillingsparadoxon nicht fehlen. Insbesondere können wir an diesem Paradoxon das Problem mit der Information über eine größere oder kleinere Raumzeitdichte klären. Die meisten anderen Paradoxa (z.B. Garagenparadoxon) sind eher uninteressant. Diese lassen sich immer über die symmetrische Sichtweise, mit der nicht vorhandenen Gleichzeitigkeit erklären. Beim Zwillings-Paradoxon ergibt sich aber kein symmetrisches Ergebnis. Dafür muss es einen Grund geben.
Bei der Mathematik gibt es keinen Unterschied. Selbst die SRT hat das Ergebnis, dass der Zwilling in der Rakete immer der jüngere ist. Das ist auch in der DP das zu erwartendes Ergebnis. In der SRT ist aber nicht klar, warum dies so ist. Da wird oft mit Symmetriebruch oder ähnliches argumentiert. Für ein besseres Verständnis erweitern wir das Zwillingsparadoxon auf Drillinge.
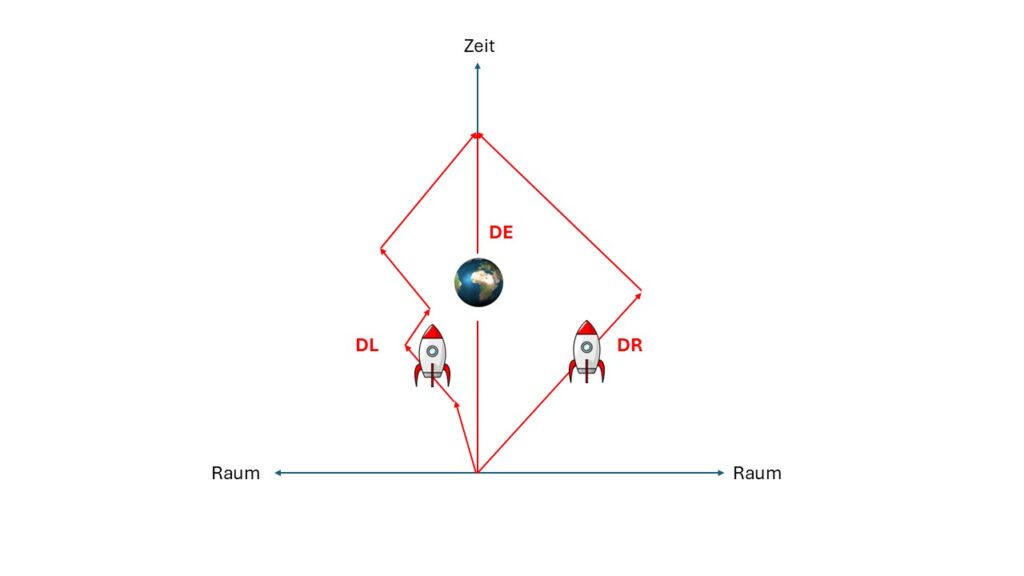
Es gibt einen Drilling links (DL), einen Drilling rechts (DR) und einen Drilling auf der Erde (DE). Dabei hat DR ein einziges Ziel und DL klappert mehrere Orte ab. DE bleibt auf der Erde und bewegt sich nur in der Zeit voran. Was im Bild evtl. nicht 100% zu erkennen ist, der zurückgelegte Weg von DL und DR sollen in Summe identisch sein.
Das Ergebnis ist klar. Die Drillinge sind beim Startpunkt gleich alt. Wenn diese sich wieder begegnen, sind DL und DR identisch alt, da Beide in Summe einen gleichlangen Weg durch die Raumzeit hatten und DE ist gegenüber den anderen der ältere.
In der DP ist das Ergebnis logisch so zu erwarten. Nur DL und DR erfahren eine Erhöhung der Raumzeitdichte. Nur bei DL und DR kann, gegenüber der Startbedingung, eine Zeitdilatation auftreten. Dabei spielt es keine Rolle, in welcher Richtung die Zeitdilatation auftritt. Nur die Summe der Zeitdilatation, dass ist die Wegstrecke, ist am Ende relevant. Es ist hier eine Information von jünger und älter oder von kleinerer und größerer Raumzeitdichte vorhanden.
Aus der SRT heraus ist das nicht klar. Die SRT ist immer symmetrisch. Damit müsste zwischen DE und DL jeweils der andere eine identische Zeitdilatation erfahren und es sollte keinen Unterschied geben. Das Ergebnis sieht aber anders aus. Warum passiert das? Ich habe dazu noch keine gute Erklärung gelesen. Was am häufigsten kommt, ist die offensichtlichste Erklärung. Wenn die Symmetrie nicht mehr gegeben ist, dann muss diese wohl verletzt worden sein. Weil nichts anderes da ist, ist der Schuldige schnell gefunden. Die böse, böse Beschleunigung. Diese muss die Symmetrie brechen. Dann kommen noch schlimmere Aussagen, wie: „Die SRT kann mit Beschleunigung nicht umgehen“. Was für ein Unsinn. Die SRT kann nur und ausschließlich nichts mit der Gravitation anfangen. Jegliche Art von klassischer Beschleunigung kann zu 100% fehlerfrei in das Diagramm oder die Berechnungen eingebaut werden.
So, jetzt wieder beruhigen und die Lösung angehen. Wenn die Information nicht schon vorher vorhanden ist, könnten wir diese auch nicht erhalten. Wir können keine zusätzliche Information erzeugen. Die Information muss schon immer enthalten sein. In der DP haben wir diese Information immer. Wir können diese in der SRT nur nicht ermitteln. Diese kann nur unter bestimmte Voraussetzung herausgeholt werden. Das ist der richtige Ansatz.
Die Beschleunigungen können es nicht sein. Wir haben die Zwillinge auf Drillinge erweitert, damit dies sichtbar wird. Wir könnte DL auch noch „zackiger“ durch die Raumzeit fliegen lassen. Wenn die Summe des zurückgelegten Weges in der Raumzeit identisch ist, sind DL und DR identisch alt. Die Anzahl und Richtung der Beschleunigungen spielen dabei keine Rolle. Die Beschleunigung ist nur zwingend notwendig, damit es überhaupt eine Veränderung, in der Raumzeitdichte gibt und die Drillinge sich wieder treffen können.
Was vielen nicht auffällt, ist, dass bei dem klassischen Zwillingsparadoxon der Zwilling im Raumschiff gleich 2 Symmetriebrüche macht. Den ersten, wenn dieser von der Erde startet. Den zweiten, wenn er vom Zwischenziel wieder startet. Dann ist der erste Symmetriebruch ein „guter“, da noch alles symmetrisch ist und der zweite Symmetriebruch ein „schlechter“ der alles kaputt macht. Mit gut und böse funktioniert Physik nicht. Das ist eine schlechte Argumentation.
Kehren wir zu den Grundelementen zurück. Wann mussten wir von einem absoluten Wert in ein Relativitätsprinzip ausweichen? Wenn wir die Referenzpunkte zur Messung verloren haben. Wollen wir mehr Information haben, dann muss es wieder einen Referenzpunkt geben, der diese Information angeben kann. Das Bild nochmals mit den zwei wichtigen Punkten.
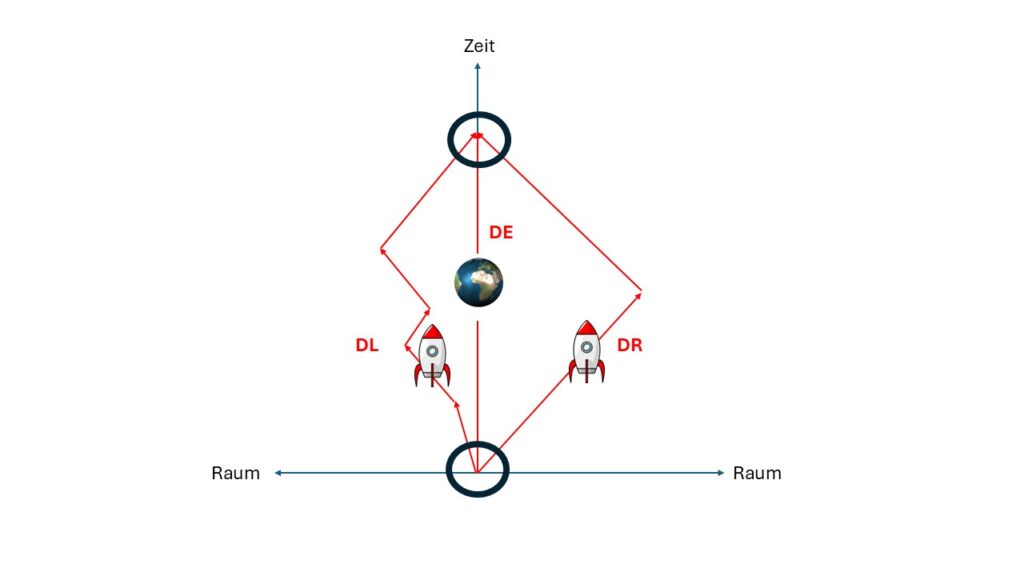
Das Besondere in diesem Paradoxon ist der Start- und der Endpunkt. Der Startpunkt ist für alle in der Raumzeit identisch. Der Endpunkt ist im Raum identisch geblieben und in der Zeit verschoben. Es sollte für die Drillinge jeweils der identische Raumzeitpunkt sein. Wir haben innerhalb des Relativitätsprinzips eine zusätzlichen Referenzpunkt für die Messung erzeugt. Damit erhalten wir alle Informationen zu Raum und Zeit, die im Relativitätsprinzip von diesem Referenzpunkt abweichen. Dann kommt auch in der SRT ein jünger und älter raus.
Bei Galileo gibt es kein kleiner oder größer. Nicht, weil der noch keine Raumzeit kannte, sondern weil es dort nur einen Referenzpunkt für alles gibt, den Nullpunkt. Um ein größer oder kleiner festzustellen, müssten wir bei Galileo auch den Nullpunkt verwenden. Genau dieser darf aber nicht mehr erkennbar sein, sonst gibt es kein Relativitätsprinzip. Daher ist die Sichtweise von Galileo tatsächlich zu 100% symmetrisch. Diese Idee wird auf die SRT von Einstein übertragen und alles, bis auf das Zwillingsparadoxon sieht gut aus. Nur beim Vergleich von zwei Raumzeiten ist ein größer oder kleiner nicht explizit ausgeschlossen. Das darf es geben. Wir können aber im Normalfall nur die Differenz zwischen den Raumzeiten erkennen. In der DP werden die lokalen Raumzeitdefinitionen verglichen. Auch hier sieht man im Normal fall nur die Differenz und alles sieht symmetrisch aus. Wir wissen allerdings, dass es ein größer und kleiner gibt. In SRT wie in der DP brauchen wir einfach nur einen zusätzlichen Referenzpunkt, um diese Information zu erhalten. Das Zwillingsparadoxon liefert diesen.
Der letzte Abschnitt in diesem Kapitel geht darauf ein, dass die Namensgebung für SRT und ART, na sagen wir mal, maximal unglücklich gelaufen ist. Die Bezeichnungen können wir nicht mehr ändern. Diese suggerieren, dass die SRT das kleine Geschwisterlein der ART ist. Dem will ich hier widersprechen. Aus rein mathematischer Sicht kann ich die Aussage noch verstehen. Aus logischer Sicht ist das einfach falsch. Auch an diesem Punkt ist klar zu erkennen, dass sehr viele mit der SRT gut rechnen können. Verstanden haben die SRT aber nur wenigsten. Wir bleiben bei dem Ansatz aus der DP.
Was macht die ART? Diese sagt aus, wie sich die Raumzeitkomponenten durch Raumzeitdichte verändern. Diese Aussage macht nur innerhalb einer einzigen Raumzeit Sinn. Die Raumzeitdichte ist dabei nur die Quelle. Die eigentliche Aussage betrifft nicht die Raumzeitdichte. Das können wir daran erkennen, dass die ART eine Singularität voraussagt. Das ist mit dem Ansatz einer Raumzeitdichte nicht möglich. Für die ART ist nur die Menge und die Verteilung der Raumzeitdichte auf die Raumzeitdimensionen interessant. Die Raumzeitkrümmung muss dann dazu ausgleichen. Die ART macht Aussagen zur Raumzeitkrümmung. Damit zum umgebenden Raum der Raumzeitdichte in einer einzigen Raumzeit. Dort können auch mehrere Raumzeitdichte, räumlich getrennt, vorhanden sein. Dies Aussage der ART betrifft die umgebende Raumzeit.
Was macht die SRT? In der alten Sichtweise werden den Objekten unterschiedliche Raumzeiten zugewiesen und diese verglichen. Damit sieht es nur so aus, dass die SRT eine Aussage zur Raumzeit trifft. Das kann die SRT gar nicht. Es werden verschiedene Raumzeit verglichen. Zu einer einzigen Raumzeit oder einem einzigen Objekt, kann die SRT keine Aussage machen. Wir brauchen immer mindestens zwei Objekte, sonst macht die SRT keinen Sinn. In der DP wird es etwas deutlicher. Die SRT vergleicht die lokale Definition der Raumzeitgeometrie von verschiedenen Raumzeitdichten. Das sind Aussagen zu einer Raumzeitdichte. Nur weil dann die restliche Raumzeit aus dieser Definition heraus anders erscheint, glauben wir, dass die SRT eine Aussage zur Raumzeit trifft. Klar in der DP ist alles Raumzeit, damit ist jede physikalische Aussage irgendwie eine Aussage zur Raumzeit.
Die SRT macht absolut keine Aussage zur umgebenden Raumzeit einer Raumzeitdichte. Diese ist nur der Vergleich von Raumzeitdichten. Die ART braucht eine Raumzeitdichte als Quelle der Raumzeitkrümmung. Die ART interessiert sich aber sonst nicht für die Raumzeitdichte und macht nur Aussagen zur umliegenden Raumzeit. Daraus folgern wir:
Die ART und die SRT ergeben zwei komplett unterschiedliche Aussage.
Die SRT ist einfach nur in der ART enthalten, weil das Relativitätsprinzip in der DP per Definition in allen physikalischen Aussagen mit eingebaut sein muss. Alles ist Raumzeitdichte und diese unterliegt immer dem Relativitätsprinzip.
Was macht denn die QM? Diese beschreibt den „inneren Aufbau“ einer Raumzeitdichte durch niederdimensionale Raumzeiten (Felder). Die QM interessiert sich aber nur für die Raumzeitdichte. Die Raumzeitdichte kennt keine Raumzeitkrümmung. Die QM benutzt die umgebende Raumzeit einer Raumzeitdichte nur als „gegebene Möglichkeit“. Ob dieser eine Raumzeitkrümmung aufweist, kann eine niederdimensionale Raumzeitdichte nicht feststellen. Damit ist die umgebende Raumzeit für die QM uninteressant. Daher lässt sich die SRT und die QM bis zu einem bestimmten Maß vereinigen. Beiden schauen sich Raumzeitdichten und nicht den umgebenden Raum an
Damit lassen wir das Kapitel hier ausklingen und schauen uns im nächsten Kapitel die ART genauer an.