
Alles besteht aus Raumzeit
Die ersten Entwicklungsschritte für die DP, waren mehrere verschiedene Startpunkte. Keiner davon war dieser Ansatz, denn wir hier aufbauen werden. Die verschiedenen Lösungswege haben sich im Laufe der Zeit in diesen Punkt vereinigt. Das war der Zeitpunkt, als aus einer Sammlung von losen Ideen, eine Theorie gebildet wurde.
Die Grundidee ist die Weiterführung eines genialen Gedankens von Einstein. Zusätzlich wird diese Idee auf ein absolutes Extrem gesetzt. Wenn die Gravitation, als reine geometrische Beschreibung in der Raumzeit abgebildet wird (Raumzeitkrümmung), dann müssen wir diese Idee „einfach“ auf alles andere übertragen.
Dann ist Alles eine geometrische Abbildung, in nur einem einzigen Objekt, der Raumzeit.
Wie kommen wir auf so eine schräge und auch extremen Idee, Alles auf nur einem einzigen Objekt abbilden zu wollen? Was wir erreichen wollen, ist die Vereinigung von ART und QM. Allerdings stellt sich diese Aufgabe als ein sehr hartnäckiger Brocken heraus. Die klügsten Köpfe versuchen dies seit über 100 Jahren und haben noch keine wirklich valide Lösung gefunden. Es werden immer mehr Stimmen laut, dass dies eventuell gar nicht möglich ist. Tatsächlich ist die Idee der Vereinigung nur ein Wunsch der Physiker. Niemand kann mit Sicherheit sagen, ob dies überhaupt möglich ist. Daher werden die Schritte zur Vereinigung immer kleiner gewählt. Es werden sehr spezielle Eigenschaften einer möglichen Vereinigung untersucht. Unser Ansatz ist das genaue Gegenteil davon.
Wir gehen davon aus, dass eine Vereinigung grundsätzlich möglich ist, und wählen aus den Möglichkeiten die extremste Form aus. Wer sich auf die Suche nach dem heiligen Gral begibt, stellt diesen nicht in Frage. Es stellt sich aber die Frage: Gibt es einen Hinweis darauf, dass der Ansatz, „Alles ein Objekt mit einer geometrischen Abbildung“ überhaupt sinnvoll ist? Naja, wenn ich schon so Frage.
Dazu starten wir im physikalischen Kindergarten und schauen uns als erstes eine kleine und bekannte Formel an.
r_{S}\space =\space \cfrac{2\space *\space G\space *\space M}{c^2}
Mit dieser Formel können wir den Schwarzschildradius einer Masse ausrechnen. Das Schwarze Loch der Masse hat dabei keine Ladung und rotiert nicht. Diese Darstellung der Gleichung ist sehr gut mit unserer Intuition vereinbar.
r_{S}\space =\space \cfrac{2\space *\space 6,6743 *\space 10^{-11}\space * \space 6\space *\space 10^{24}}{299792548^2}
Bei der Erde kommen wir auf ca. 9mm. Die Maßeinheiten habe ich einfach weggelassen. Das Ergebnis ist eine Länge. Alle sehr einfach gehalten. Das ist eine Gleichung und damit eine Identität. Auf der rechten Seite muss auch eine Länge stehen. Das erkennen wir auf den ersten Blick nicht, da die einzelnen Bestandteile keine Länge sind. Das heißt, obwohl auf der rechten Seite die Gravitationskontante, die Masse und die Lichtgeschwindigkeit alles keine Längen sind, dürfen wir diese zu einer Länge kombinieren. Jetzt der physikalische Kindergarten. Wieso dürfen wir dies den machen? Das sind sehr unterschiedliche Objekte und nichts davon ist eine Länge. Wir überlegen da nicht lange. Wenn die Maßeinheiten identisch sind, dürfen wir beide Seiten Vergleichen. Daher können wir den Schwarzschildradius auch mit anderen Objekten beschreiben. Wir müssen „nur“ eine Länge mit dem identischen Ergebnis erhalten.
Daher wählen wir jetzt eine eher ungewöhnliche Darstellung aus.
r_{S}\space =\space \cfrac{2\space *\space l_P^2}{\lambda_C}
Mit l_P ist eine Planck-Länge und mit \lambda_C eine Compton-Wellenlänge gemeint. Hier brauchen wir die Compton-Wellenlänge der Erde. Falls jemand dies nachrechnen will, alle Planck-Einheiten und das h sind bei mir immer nicht reduziert (nicht durch 2\space *\space \pi geteilt). Bei der Compton-Wellenlänge nehmen wir einen Streuwickel von 90 Grad an, damit der Cosinus aus der Formel rausfällt. Dann ergibt sich:
r_{S}\space =\space \cfrac{2\space *\space 1,6413\space *\space 10^{-69}}{3,6837\space *\space 10^{-67}}
Wir erhalten wieder unsere ca. 9mm. Dieses Mal haben wir nur Längen benutzt. Scheint doch viel „natürlicher“ zu sein. Die verwendeten Längen sind aber die Planck-Länge und die Compton-Wellenlänge. Das sind Objekte aus der QM und nicht aus der ART. Funktioniert trotzdem. Mit dieser anderen Darstellung erhalten wir zusätzliche Informationen.
Beispiel: Wir wissen, dass es keine Compton-Wellenlänge, kleiner als die Planck-Länge geben kann. Sonst müsste die Energie bei der Streuung direkt zu einem Schwarzen Loch führen. Wenn wir in die obige Formel statt einem \lambda_C ein l_P eintragen, dann kommt als unterste Grenze, eine Schwarzschildradius von zwei Planck-Längen raus. Für einen Schwarzschildradius scheint dies eine untere Grenze zu sein. Aus der ersten Darstellung können wir diesen Zusammenhang nicht erkennen. Das wir verschieden Darstellungen wählen können ist damit sehr gut für uns.
Wir können eine weitere Darstellung wählen. Hier ist M_E die Masse der Erde und m_P die Planck-Masse.
r_S\space =\space 2\space *\space l_P\space *\space \cfrac{M_E}{m_P}
r_S\space =\space 2\space *\space 4,0513\space *\space 10^{-35}\space *\space \cfrac{6\space *\space 10^{24}}{5,4555\space *\space 10^{-8}}
Wir erhalten wieder unser ca. 9mm. In dieser Darstellung sieht es so aus, dass der Schwarzschildradius nur eine doppelte Planck-Länge (also der kleinste mögliche Wert) ist, welche um den Faktor eines Masseverhältnisses verändert wird. Da der Schwarzschildradius nicht kleiner als zwei Planck-Längen ausfallen darf, kann eine Masse kleiner als die Planck-Masse kein Schwarzes Loch bilden. Wieder eine neue Information. Irgendwie können wir immer auf eine Darstellung mit Länge und Masse kommen. Wir können die letzte Formel etwas umstellen und erhalten:
\cfrac{r_S}{l_P}\space =\space \cfrac{2\space *\space M_E}{m_P}
Nun ist es ein Längenverhältnis zu einem Masseverhältnis ohne eine Maßeinheit beim Vergleich. Es scheint so, dass Abbildungen in unserer Raumzeit, wie z.B. ein Schwarzschildradius oder eine Masse, sich an bestimmte Grenze zu halten haben.
Machen wir dazu ein zweites bekanntes Beispiel. Jetzt starten wir aber gleich mit einer Formel für eine Angabe eines Verhältnisses. Also einem Ergebnis ohne eine Maßeinheit.
F_{Elekt}\space =\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space r^2}
F_{Grav}\space =\space \cfrac{G\space *\space m_1\space *\space m_2}{r^2}
Die erste Formel ist die klassische Beschreibung der statischen elektrischen Kraft. Die zweite Formel ist die klassische Beschreibung der Gravitation als Kraft. Vermutlich hat mit den nächsten Schritten niemand ein Problem. Wir setzen für m_1 und m_2 die Masse eines Elektrons ein und für die Ladung e die Elementarladung des Elektrons. Dann setzen wie die zwei Gleichungen ins Verhältnis, denn beide Gleichungen haben die identische Maßeinheit.
\cfrac{F_{Elekt}}{F_{Grav}}\space =\space \cfrac{\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space r^2}}{\cfrac{G\space *\space m_1\space *\space m_2}{r^2}}
Das r^2 kürzt sich raus und dann noch die Zahlen rein. Das ergibt:
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space G\space *\space m_e^2 }\space =\space 4\space *\space 10^{42}
Das ist eine extrem große Zahl. Damit ist der Unterschied der Kräfte von Gravitation und elektrischem Feld eine Zahl mit 42 Nullen. Das können wir π mal Daumen überprüfen. Wie nehmen einen kleinen schwachen Kühlschrankmagneten und ziehen damit eine metallische Büroklammer in die Höhe. Ergebnis ist, dass der Magnet eine stärkere elektrische Kraft ausübt als die gesamte Erde mit ihrer Gravitation. Das Ergebnis ist richtig und wird von allen Physikern akzeptiert. Falls Ihr dazu eine andere, auf jeden Fall kleinere Zahl, gesehen habt, ist dies kein Problem. Es kommt darauf an, welches Teilchen für die Masse benutzt wird. Wir nehmen das Elektron, da dies von der Masse her, das kleinste Teilchen mit einer Ladung ist. Die berechnete Zahl mit dem Elektron brauchen wir später auch wieder.
Wir haben hier die Gravitation als Kraft und das elektrische Feld als Kraft vergleichen. Dabei sollten doch genau diese Grundkräfte nicht vereinbar sein. Da können jetzt viele Einwände kommen. Ist nur die alte klassische Physik, Gravitation ist keine Kraft, kein Beispiel aus der QM, usw. Alle Einwände sind richtig. Es gilt das Prinzip des ersten Beispiels: Wenn die Maßeinheiten übereinstimmen, können wir die mathematischen Ausdrücke vergleichen. Das Prinzip gilt für alle Maßeinheiten und davon gibt es sehr viele. Es spielt keine Rolle, woher die Beschreibung als Formel gekommen ist. Wenn wir es schaffen, dass die Maßeinheiten übereinstimmen, können wir dies vergleichen.
Hier können wir wieder eine ungewöhnliche Darstellung wählen. Mit \alpha als die Feinstrukturkonstante.
\cfrac{F_{Elekt}}{F_{Grav}}\space =\space \cfrac{1}{2\space *\space \pi}\space *\space \alpha\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2\space \iff\space \cfrac{F_{Elekt}\space *\space 2\space *\space \pi}{F_{Grac}\space *\space \alpha}\space =\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Keiner der einzelnen Terme hat eine Maßeinheit und es passt trotzdem alles zusammen. Ein Kräfteverhältnis, mit einem Korrekturfaktor je Kraft, ist nichts weiter als ein Masseverhältnis zum Quadrat. Wenn Ihr euch an die erste Formel erinnert, dann könnten wir auch das Quadrat der Schwarzschildradien benutzen. Es sieht so aus, dass wir hier fast beliebige Darstellungen für die identische Aussage wählen können.
Wir versuchen unsere Erkenntnisse aus den zwei Beispielen in eine neue Idee zu formulieren. In der Physik gibt es nur ein Objekt und die Maßeinheit ist nur eine bestimmte Sichtweise auf dieses Objekt. Wir betrachten das identische Objekt und setzten verschiedene Brillen auf. Dann ist es logisch, dass wenn wir Terme, die wir per Umformung auf identische Maßeinheit gebracht haben, vergleichen können. Es ist alles das Gleiche.
Bei einer Vereinigung von ART und QM sind diese Maßeinheiten sehr unterschiedlich. Bei der ART ist in der Raumzeitkrümmung eine Länge vorhanden. Bei der QM eine Wahrscheinlichkeit. Eine Wahrscheinlichkeit ist aber gar keine Maßeinheit. Das sind sehr unterschiedliche Brillen. Hier liegen das Problem und die Lösung. Obwohl wir mit der Idee von nur einem einzigen Objekt starten, werden wir feststellen, dass die QM etwas komplett anderes betrachtet als die ART. Daher wird es eine Vereinigung, als mathematisch identische Beschreibung, nicht geben. Auf der logischen Ebene werden beide Theorien in ein vollumfängliches einheitliches Framework eingebunden, die Dimensionale Physik.
Irgendeinen „Anker“ als Startpunkt müssen wir setzen. Wir wollen keine komplett neue Beschreibung, wie die Stringtheorie erzeugen. Wir wollen hier die gegebenen Beschreibungen der ART und der QM vereinigen. Die Idee ist es, mit nur einem einzigen Objekt zu arbeiten. Tatsächlich ist mit der ART die erste Hälfte bereits erledigt. Daher starten wir, entgegen dem gesamten Mainstream in der Physik, bei der ART. Da wir von der ART aus starten holen wir uns die charakteristische Gleichung für die ART, in der einfachsten Form. Die Feldgleichungen von Einstein.
G_{\mu\nu}\space =\space k\space *\space T_{\mu\nu}
Schauen wir uns die Struktur der Gleichung etwas genauer an.
Das Erste, was auffällt: Wieso den Feldgleichungen? Da steht nur eine Gleichung. Diese Schreibweise ist sehr kompakt. Dort stehen 16 einzelne Gleichungen, die zusammen ein Gleichungssystem ergeben. Die griechischen Buchstaben μ und ν zählen von 0 auf 3 hoch (das ist so Konvention). Jeder Buchstabe steht für die Anzahl der Dimensionen in unserer Raumzeit. Man zählt im Lehrbuch für unsere Raumzeit 4 Dimensionen. Drei Raumdimensionen und eine Zeitdimension. Tatsächlich sind es in der Gleichung 4 Raumdimensionen. Die Zeitdimension erhält einen zusätzlichen Faktor, welcher aus einer Zeit eine Länge macht. Die Maßeinheit der Zeitdimension ist in der mathematischen Beschreibung eine Länge und keine Zeit. Die Zeitdimension bekommt ein anderes Vorzeichen als die Raumdimensionen. Raumdimensionen ein Plus und die Zeitdimension ein Minus oder umgekehrt. Wie herum dies gemacht wird ist reine Ansichtssache. Wichtig ist, dass die Vorzeichen unterschiedlich sind. Das nennt sich Signatur der Raumzeit. Wir verwenden die Signatur (- + + +). Die Großbuchstaben sind Tensoren. Dort wird beschrieben, wie sich der Inhalt der Tensoren, von einer Dimension zur anderen Dimension verhält. Daher kommen 4 * 4 Möglichkeiten = 16 Gleichungen heraus. Auf Grund von Symmetrien benötigt man aber nur 10 unabhängige Gleichungen.
Wir werden hier, entgegen dem Lehrbuch, nur noch die echten Raumdimensionen, also die mit +, zählen. Damit ist unsere Raumzeit 3D. Warum wir dies tun, klärt sich im Kapitel 3 „Grenzen der Raumzeit“. Die zusätzliche Zeitdimension ergibt sich automatisch zu jeder beliebigen Raumzeitkonfiguration. Wir werden sehen, dass diese Signatur allein, für eine Klassifizierung der Raumzeit, nicht ausreichend ist.
Die linke Seite der Gleichung hat nur den Tensor mit der Bezeichnung G, den Einstein-Tensor. Dieser beschreibt, nennen wir es mal ganz allgemein, eine Verformung der Raumzeit selbst. Diese Art der Verformung wird als Raumzeitkrümmung bezeichnet. Die Raumzeitkrümmung wird in der ART mit der Gravitation gleichgesetzt. Damit ist die Gravitation keine Kraft oder Wechselwirkung, sondern eine geometrische Abbildung auf genau einem einzigen Objekt, der Raumzeit. Unser Ansatz ist, eine geometrische Identität über alle Betrachtungen hinweg auf ein Objekt zu erhalten. Damit ist für die Gravitation die gewünschte Form der Beschreibung bereits erreicht. Daraus folgt sofort die Frage, ob wir dies für die andere Seite der Gleichung auch so hinbekommen.
Wir übertragen den Gedanken, einer Abbildung in der Raumzeit, auf die andere Seite der Gleichung. Dort haben wir zwei Elemente. Als erstes das kleine k. Dies ist eine Proportionalitätskonstante. Diese beinhaltet ausschließlich feste Werte und stellt damit, im mathematischen Sinn, nur eine feste Zahl mit der passenden Maßeinheit dar. Wir werden dieses k später untersuchen. Dann gibt es noch den Energie-Impuls-Tensor T. Dieser beinhaltet alles, was man als Masse-Energie-Äquivalent bezeichnet. Wie bei G auf die jeweiligen Dimensionen zueinander aufgeteilt.
Ohne es bemerkt zu haben, ist das Ziel schon erreicht. Dabei sieht es nach dem Gegenteil aus. Der Energie-Impuls-Tensor ist eine wilde Sammlung aus allem, was das Universum zu bieten hat ohne die Gravitation. Wie kann eine Gleichung mit einer Sammlung, von dermaßen unterschiedlichen Objekten, eine so klare Darstellung erhalten? Weil die Sammlung gar nicht so wild ist, wie diese aussieht. Wir drücken mal alle und ich meine damit auch wirklich alle mathematischen Augen und Hühneraugen zu und schauen uns die Gleichung als Vereinigung von ART und QM an. G beschreibt die Gravitation und T sammelt den gesamten Teilchen-Zoo aus dem Standardmodell, zuzüglich Impuls, Ladungen usw. ein. Wir wissen, dass die Beschreibungen nicht übereinstimmen, und haben hier trotzdem ein Gleichheitszeichen stehen. Damit diese Gleichung funktioniert und sich der Unterschied zur QM ergibt, muss die ART eine spezielle Sichtweise auf diese Sammlung von Masse-Energie-Äquivalenten annehmen. Die Unterschiede müssen normiert werden oder salopp ausgedrückt, die rechte Seite muss die richtige Brille aussetzen. Das geht wie so oft in der Physik über die Energie. Egal wie verschieden die Beiträge aus dem Energie-Impuls-Tensor sind, die ART muss eine normierte Sichtweise annehmen. Die ART darf sich nur für zwei Dinge aus T interessieren. Die Menge an Energie und die evtl. vorhandene Ausrichtung auf die Dimensionen. Jegliche „innere Struktur“ eines Masse-Energie-Äquivalent (ist es ein Elektron, Photon, Proton usw.) muss ausgeblendet werden.
Das ist eine Gleichung. Daher stehen auf beiden Seiten die identischen Maßeinheiten. Der Einstein-Tensor verwendet nur die Raumzeit mit einer Verformung. Die Maßeinheit ist eine Angabe einer Länge. Dann machen wir dies beim Energie-Impuls-Tensor auch so. Eine geometrische Abbildung in der Raumzeit mit der Maßeinheit einer Länge. An diese geometrische Abbildung im Energie-Impuls-Tensor werden bestimmte Anforderungen gestellt. Die Gleichung muss weiterhin funktionieren und alle Aussagen der ART zur Gravitation müssen sich daraus ergeben. Für einen Teil der Aussagen muss bereits auf diesem Level die Abbildung zur QM passen. Das klingt nach einer sehr schwierigen geometrischen Abbildung in der Raumzeit. Genau das Gegenteil ist der Fall. Wir werden eine, in einem bestimmten Raumzeitvolumen, gleichverteilte „Dichte“ der Raumzeit selbst annehmen. Die Verformung der Raumzeit für die Gravitation trägt den Namen Raumzeitkrümmung. Dann brauchen wir für die Verformung auf der anderen Seite der Gleichung auch einen Namen.
Daher, Kraft souveräner Willkür => Die Verformung der Raumzeit für ein Masse-Energie-Äquivalent heißt: Raumzeitdichte. Dabei bezeichnet „Dichte“ diese Verformung an bestimmten Stellen sehr gut und an andere Stelle ist dies eher hinderlich. Der Name Dichte ist intuitiv mit der Alltagserfahrung belegt. Die Dichte der Raumzeit ist anders definiert als die Dichte einer beliebigen Substanz. Irgendeinen Namen müssen wir aber vergeben. Damit bleibt es bei Raumzeitdicht als Quelle der Raumzeitkrümmung.
Zu einer kompletten Beschreibung der Physik brauchen wir nur 4 Annahmen:
Wir werden sehen, dass uns die Folgerungen aus diesen Annahmen, zu der uns bekannten Beschreibung der Physik führen werden. Hätte mir jemand dies vor Entwicklung der DP gesagt, hätte ich diese Person für Verrückt gehalten. Dieser Ansatz hat aber, für die Überprüfung der DP, einen großen Vorteil. Es gibt für die Schlussfolgerungen fast keine Wahlmöglichkeit. Entweder die Logik ist richtig oder die gesamte Theorie fällt in sich zusammen. Es gibt nur sehr wenige Stelle, wo es noch einen Spielraum für „Erweiterungen“ gibt. Die Möglichkeiten wie bei anderen Theorien, mit kleineren Strukturen, höherer Energien, höheren Masse, weitere Teilchen, Symmetriebruch usw. sind hier nicht gegeben.
Die Raumzeit als Substanz, mit den Eigenschaften der Kontinuität und der Differenzierbarkeit, könnten wir sogar aus der Annahme der Raumzeitdichte rausholen. Wir lassen unseren Ansatz auf diese 4 Punkte verteilt stehen. Das ist für das Verständnis besser. Damit ist die einzige wirkliche zusätzliche Annahme zur bekannten Physik die Raumzeitdichte. Was soll sich da schon groß ändern? Fast alles, ohne die Mathematik wirklich anpassen zu müssen. Wie gesagt, klingt schon etwas verrückt.
Wir haben die Raumzeitdichte in die Welt gesetzt. Dann sollten wir zwei Dinge als erstes erledigen:
Machen wir uns das Leben nicht schwerer als es ist und starten mit etwas bekannten. Die Raumzeitkrümmung ist seit über 100 Jahren bekannt und mathematisch gut verstanden. Die Raumzeitdichte ist die Quelle einer Raumzeitkrümmung. Damit können wir die Raumzeitkrümmung als Reaktion der Raumzeit auf die Raumzeitdichte sehen. Dieses Verhalten wird durch die Feldgleichungen beschrieben. Die Definition der Raumzeitdichte muss mit den bereits gegebenen Lösungen der Feldgleichungen übereinstimmen.
Wir benutzen in diesem Text immer die Lösung der Feldgleichungen nach Schwarzschild. Das hat Vorteile aber auch Nachteile. Der große Vorteil ist, dass diese Lösung die einfachste ist. Schwarzschild hat nur wenige Monate nach der Veröffentlichung von Einstein diese Lösung gefunden. Diese ist eine Vakuumlösung für nicht rotierende Massen. Wir sind uns sicher, dass dies eine starke Vereinfachung ist. Für unsere Zwecke aber ausreichend.
Damit wir die Lösung verstehen, müssen wir die Signatur der Raumzeit (- + + +) vollständig hinschreiben. Die Signatur ist nur eine Kurzform einer Metrik. Die Metrik der Raumzeit definiert zu den Feldgleichungen das Verhalten der Raumzeit. Wenn man so will, ist die Metrik die Lösung der Gleichung. 4 x 4 Einträge für alle verschiedenen Aufteilungen zwischen den Dimensionen. Für uns gleich extrem wichtig: Die Metrik ist die passende Definition der Geometrie für die Raumzeit. Schwarzschildmetrik:
\begin{pmatrix} -c^2(1\space -\space \cfrac{r_S}{r} )dt^2 & 0 & 0 & 0 \\ 0 & +\space \cfrac{1}{(1\space -\space \cfrac{r_S}{r})}dr^2 & 0 & 0 \\ 0 & 0 & +\space r^2d\theta^2 & 0 \\ 0 & 0 & 0 & +\space r^2sin^2(\theta)d\phi^2 \end{pmatrix}
Keine Panik, sieht schlimmer aus als es ist. In der Diagonale dieser Matrix sieht man als erstes die Vorzeichen aus der Signatur (- + + +). Dahinter gibt es aber jeweils einen Term. Die beiden letzten Terme mit θ oder φ sind für uns gerade nicht relevant. Diese Lösung basiert auf Kugelkoordinaten. Die letzten beiden Angaben geben die Position auf einer Kugeloberfläche an. Wie auf der Erdoberfläche der Längen- und Breitengrad. Uns interessiert hier aber nur der Abstand, also der Radius dieser Kugeloberfläche und nicht die Position darauf. Bei der Gravitation ist die Wirkung zum Glück nur vom Abstand abhängig. Damit sind nur noch die ersten beiden Terme interessant.
Der erste Term ist die Zeitdimension. Das sieht man durch dt^2 und dem Minus. Dieser Term wird aber mit ein c^2 multipliziert. Die Geschwindigkeit ist eine Länge durch Zeit und die Zeitdimension nur eine Zeit. Bleibt nach dem Kürzen nur noch eine Länge übrig. Die Zeitdimension wird in der mathematischen Betrachtung in eine Raumdimension umgewandelt. Es sind 4 Raumdimensionen. Wir bleiben bei der Bezeichnung aus den Lehrbüchern und sage trotzdem Zeitdimension. Das kleine r ist der Abstand von der Gravitationsquelle und das r_S ist der Schwarzschildradius. Der Ereignishorizont des Schwarzen Loches.
Der zweite Term ist der radiale Abstand zur Gravitationsquelle. Jetzt muss man kein mathematisches Genie sein, um zu erkennen, dass der zweite Term zum ersten Term der Kehrwert ist. Dies bedeutet, dass sich die Zeitdimension und die Raumdimension im gleichen Maße aber entgegengesetzt verhalten. Ist man von der Gravitationsquelle weit weg, dann ist der Abstand r von r_S groß und der Bruch \frac{r_S}{r} geht in der Zeit- und Raumdimension gegen null. Damit steht in der Klammer eigentlich nur eine 1 und wir haben eine flache Raumzeit und keine Gravitation. Die Gravitation wird aber niemals exakt null. Das bedeutet für die Gravitation eine unendliche Reichweite. Nähert man sich r_S, dann geht der Bruch gegen 1. Beim Schwarzschildradius ist dieser exakt 1. Bei der Zeitdimension wird die Klammer zu null. Die Zeitdimension hat dann keine Ausdehnung/Länge mehr. Die Zeit steht für einen entfernten Beobachter still. Bei der radialen Raumdimension geht die Klammer auch gegen null. Es wird dann aber durch null dividiert und man erhält eine Singularität. Einen Wert von Unendlich oder besser nicht definiert. Das ist ein weiterer Nachteil der Schwarzschildmetrik. Bei anderen Metriken tritt diese Singularität am Ereignishorizont nicht auf. Man kann zeigen, dass dies nur eine Besonderheit dieser Metrik ist, ein mathematisches Artefakt. Da die Klammer bei der radialen Komponente im Nenner steht, geht die Ausdehnung/Länge vor dem Schwarzschildradius gegen Unendlich.
Spannt die Zeit- und die Raumdimension ein Rechteck auf passiert folgendes:
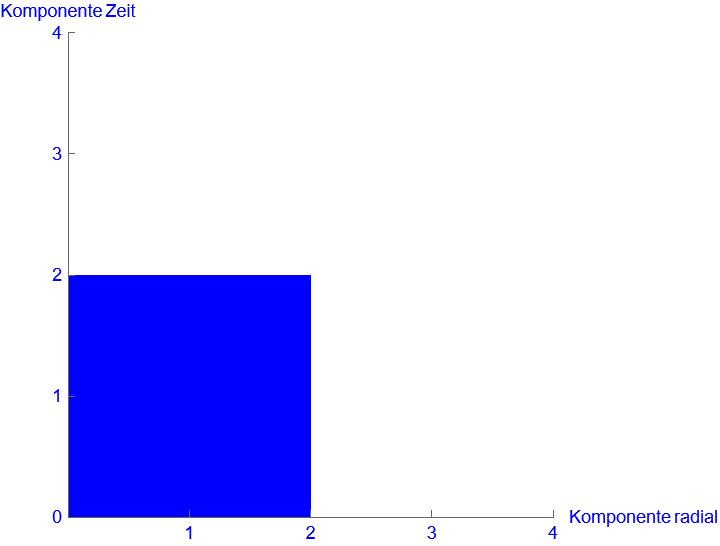
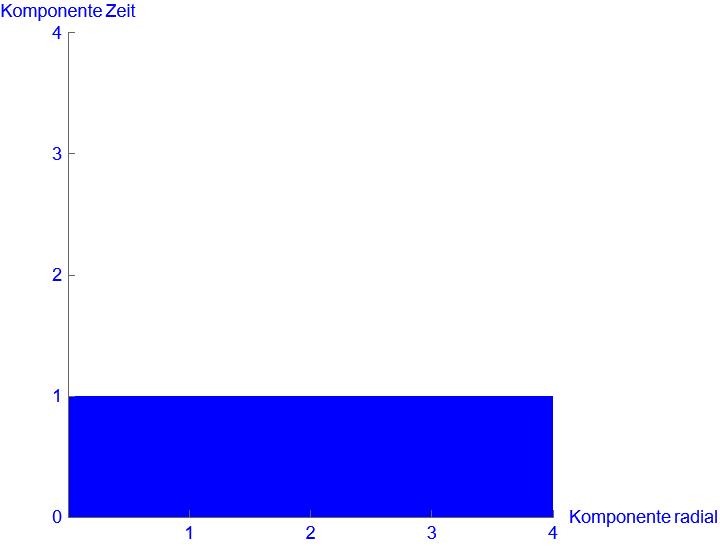
Die Zeitdimension wird kleiner und die Raumdimension im gleichen Maße größer. Das Entscheidende in der Betrachtung ist, dass der Flächeninhalt des Rechteckes sich nicht verändert. Halbiert sich die Zeit, verdoppelt sich die Länge => Identische Fläche. Diese Betrachtung der Raumzeitkrümmung reicht aus, damit wir unsere Verformung als Quelle der Raumzeitkrümmung, die Raumzeitdichte begründen können.
Bleiben wir bei einem kugelsymmetrischen Beispiel. Wenn die radiale Raumkomponente in Richtung der Gravitationsquelle immer länger wird, wo geht dann diese zusätzliche Länge hin? Was man oft hört, ist: In die Raumzeitkrümmung. Wir wollen die Raumzeitkrümmung als Reaktion zur Raumzeitdichte beschreiben. Wir drehen daher die Argumentation um. Es ist einfacher, wenn wir annehmen, dass sich die Raumzeit der Gravitationsquelle mit irgendeiner Verformung verkürzt hat. Die Raumzeitkrümmung muss dies durch zusätzlich Länge ausgleichen.
Wenn man so will, füllt die Raumzeitkrümmung, wegen der Kontinuität der Raumzeit, die fehlende Ausdehnung der Raumzeit zur Raumzeitdichte auf.
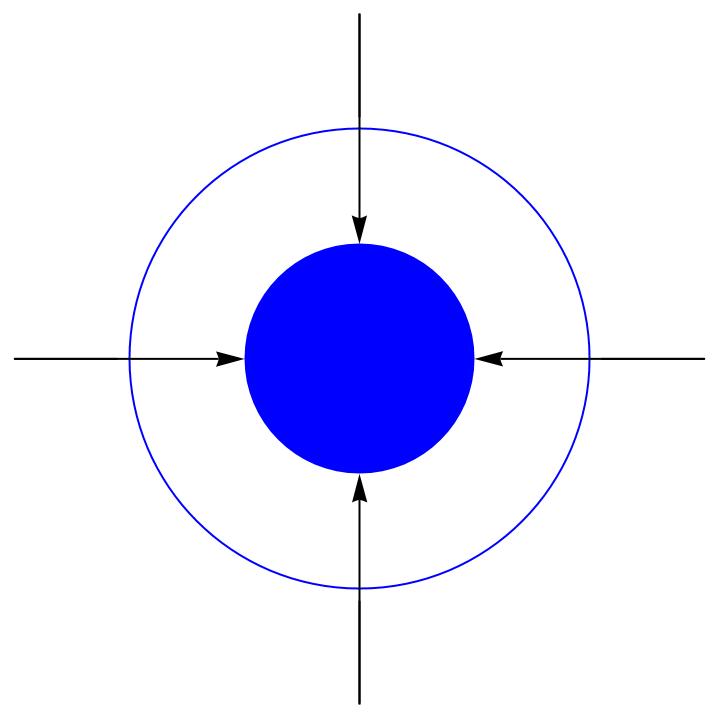
Wir betrachten ein Raumzeitvolumen und haben noch die Kugelkoordinaten. Bei einem Raumzeitvolumen darf aber nicht nur eine Länge durch Verformung kürzer werden. Das gesamte Raumzeitvolumen der Gravitationsquelle muss kleiner werden. Wir gehen weiterhin vom identischen Verhalten der Raumzeit bei einer Verformung aus. Dann muss sich zu der radialen Raumdimension auch die Zeitdimension im gleichen Maße verändern. Hier nicht gegenläufig, sonst bekommen wir kein kleineres Volumen. In diesen Fall muss sich die Zeitdimension im gleichen Maße wie die Raumdimension verkürzen.
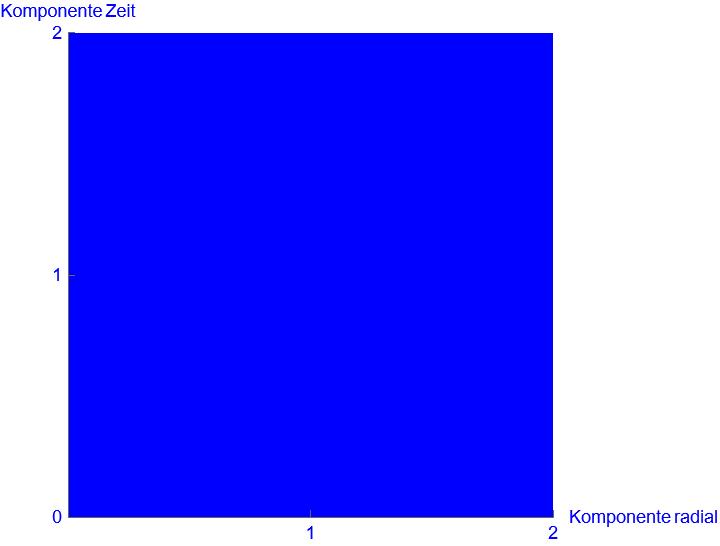
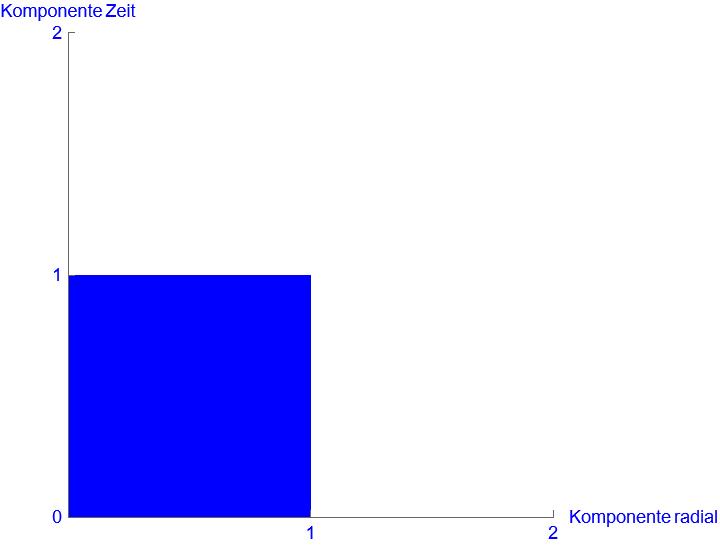
Die Verformung der Raumzeit für die Gravitationsquelle sieht wie eine „Dichte“ aus. Die vorher größere Fläche muss nun auf einer kleineren Fläche untergebracht werden.
Daher der Name: Raumzeitdichte
Wie muss man sich diese Dichte vorstellen? Bei einem Material, wie z.B. einen Schwamm, kann man diesen zusammenquetschen und eine Dichte sehr einfach erkennen. Passiert dies mit der Raumzeit so auch? Klares, nein! Bei einer Dichte nimmt man gerne die Analogie einer Substanz. In einer Substanz kann man die Dichte von außen erkennen und auch in der Substanz selbst feststellen. Wie bei dem Schwamm. Die Analogie Substanz ist wie das Wort Dichte. Mal passt es und dann wieder nicht. Genau hier passt weder Substanz noch Dichte zum umgangssprachlichen Gebrauch. Denn es wird nichts „gequetscht“. Wir haben in den Bildern oben einfach die Längen gekürzt. Das passiert nicht. Was wirklich passiert ist, dass sich die Definition der Geometrie verändert hat.
Der Umstand, dass sich die Definition der Raumzeitgeometrie verändert und nichts gezogen oder gequetscht wird, kann gar nicht oft genug erwähnt werden. Diese ist eine zentrale Stelle, für das Verständnis der DP. Wir zeichnen die zwei Bilder zur Raumzeitdichte nochmal mit den richtigen Einteilungen auf den Koordinaten. Dann sieht es so aus:
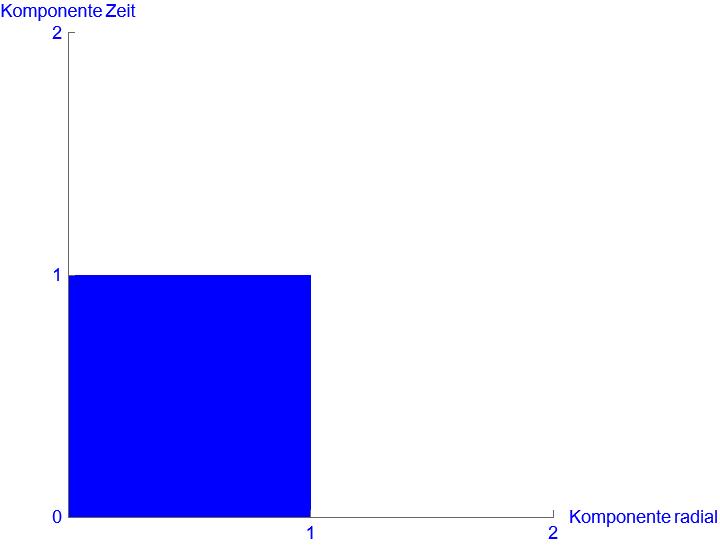
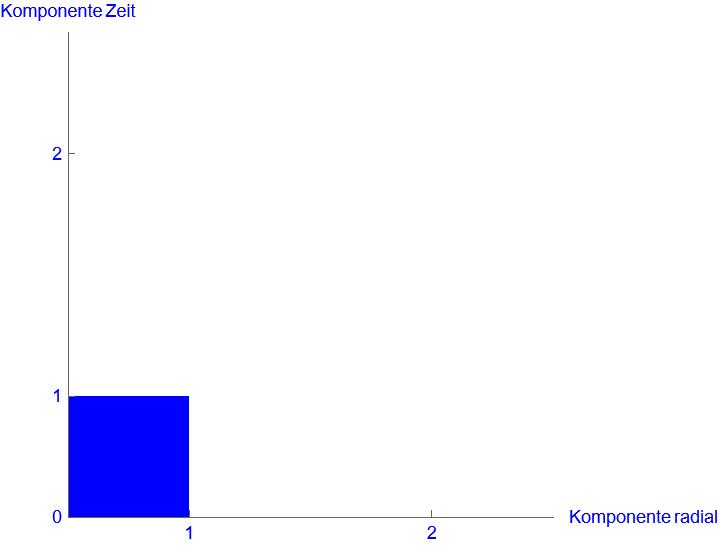
Seht Ihr den Unterschied. Die Schrittweite einer Längeneinheit bleibt in beiden Bildern eine 1. Was sich hier wirklich verändert hat ist, wie für eine Raumdimension ein Meter und für die Zeitdimension eine Sekunde definiert ist. Dies nur innerhalb der Raumzeitdichte. Das bedeutet, dass man in jedem Rechteck die Fläche 1 hat. Lokal keine Veränderung. Nur im Vergleich zwischen den Rechtecken kann man erkennen, dass damit die Definition von Zeit und Länge unterschiedlich sein muss.
Die Raumzeitdichte ist eigentlich eine „Dichte der Definition der Geometrie der Raumzeit“ oder eine „Dichte der Raumzeitdefinition“. Das werden lange Bezeichnungen oder undurchsichtige Abkürzungen. Wir bleiben bei Raumzeitdichte.
Fünf Mal fettgedruckt „Definition“. Ich hoffe das hat sich eingeprägt. Es wird nichts verdichtet wie bei einer Substanz. In der Metrik der Raumzeit gibt es keine klassische Dehnung oder Dichte. Die Definition, was die Längeneinheit 1 Meter oder die Zeiteinheit 1 Sekunde ist, wird verändert. Diese kürzere Definition ist die höhere Dichte. Nur mit der Sichtweise über die Definition können wir später ein Relativitätsprinzip aufbauen und die wichtige Schlussfolgerung der „Grenzen der Raumzeit“ herleiten.
Wir können diesen auch beim Schwamm machen.






Das eben gesagte zur Raumzeitdichte gilt auch für die Raumzeitkrümmung. Hier die Raumzeitkrümmung mit den richtigen Einteilungen bei der Zeichnung:
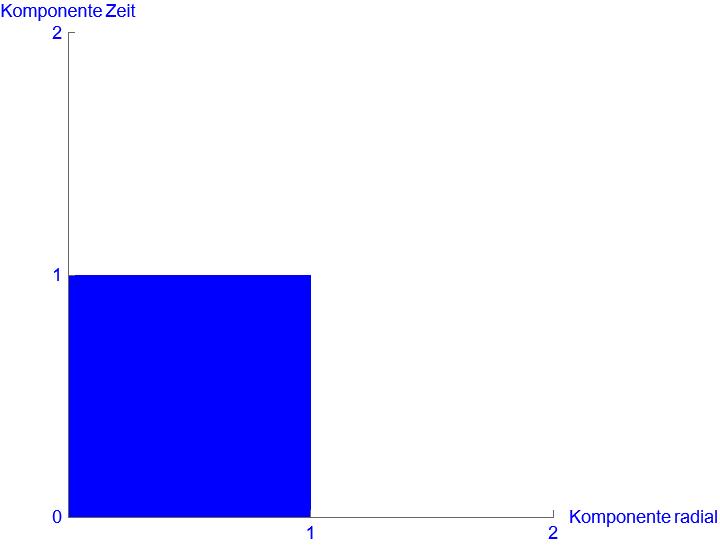
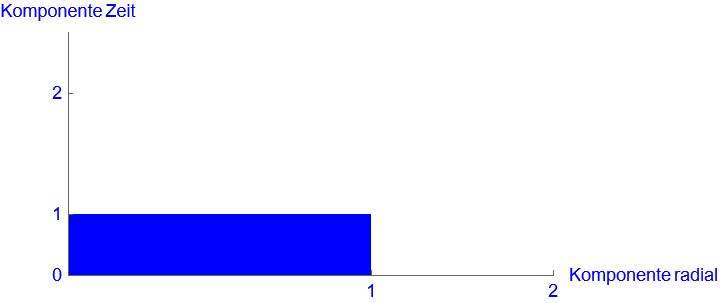
Es gibt noch mehr Namen zu definieren. In der SRT ist man bei den einzelnen Komponenten auf Längenkontraktion und Zeitdilatation gekommen. Diese Bezeichnungen benutzen wir genau so weiter. Für die Raumzeitdichte auf der Zeitdimension die Zeitdilatation und auf der Raumdimension die Längenkontraktion. Bei der Raumzeitkrümmung wird die Zeitdimension auch kleiner definiert, damit ist dies eine Zeitdilatation. Für die Veränderung der Raumdimension bei der Raumzeitkrümmung gibt es aber keine separate Bezeichnung. Hier wird dann oft direkt der Begriff Raumzeitkrümmung benutzt. Raumzeitdichte und Raumzeitkrümmung verwenden wir ab jetzt nur noch für das Verhalten der gesamten Raumzeit. Damit wir in der gleichen Syntax bleiben, werden wir für die Veränderung auf der Raumdimension bei der Raumzeitkrümmung den Begriff Längenrelaxation benutzen.
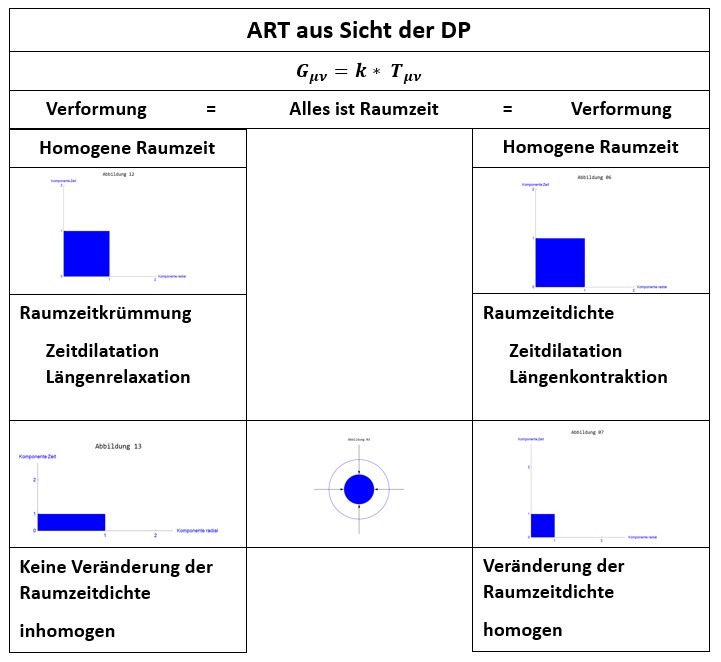
Jedes Individuum, ein Planet oder auch jedes einzelne Elementarteilchen sind eine Raumzeitdichte in nur einem einzigen Objekt, der Raumzeit. Diese ist kontinuierlich. Es gibt keine Grenzen innerhalb einer Raumzeit. Laut der DP sind wir alle zusammen und physikalisch vollkommen korrekt nur unterschiedliche Raumzeitdichten eine einzige Raumzeit. Damit stellt dieser Ansatz den wohl stärksten kollektiven Gedanken dar, denn wir ansetzen können.
Die QM wird dazu eine etwas andere Meinung haben. Für die ART stimmt dies aber zu 100%. Diesen kollektiven Gedanken sollten wir immer im Kopf haben, wenn wir Umgang mit anderen Individuen haben. Laut der DP ist dies immer ein Umgang mit uns selbst. Der Gedanke ist genauso schön wie auch erschreckend.
Am Ende dieses Kapitels wollen wir unsere Annahme der Raumzeitdichte auf hoher Flugebene prüfen. Wir müssen nur auf Grund der Geometrie das Verhalten der ART erklären können. Die Mathematik, das Wie wird nicht geändert. Unser Ziel ist es das Warum zur Mathematik erklären zu können. Die Annahmen, welche zur SRT und ART führten, Relativitätsprinzip, Lichtgeschwindigkeit und das Äquivalenzprinzip werden in separaten Kapiteln besprochen. Das wird die eigentliche Prüfung werden. Diese Annahmen müssen wir aus unserem Ansatz heraus erzeugen können. Diese können wir nicht wieder verwenden, sonst erhalten wir einen Ringschluss. Der Startpunkt war bereits die ART. Gehen wir einige Punkte durch.
Die Raumzeitkrümmung ist bei uns die Reaktion der Raumzeit auf die Raumzeitdichte. Da sich die Raumzeitdichte „zusammenzieht“, muss die Raumzeit als Kontinuum dies ausgleichen. Die Raumzeitkrümmung muss sich zwingend in Richtung der Raumzeitdichte ausrichten. Die Raumzeitdichte hat im ersten Ansatz keine Richtung. Eine Dichte kann gleichverteilt über das Volumen beschrieben werden. Damit ist die Raumzeitkrümmung eine vektorielle Größe und die Raumzeitdichte eine skalare Größe. Im nächsten Kapitel werden wir noch herleiten, dass eine Raumzeitdichte skalar und vektoriell sein kann.
Wir können die Formel der Feldgleichungen umstellen. Wir bringen den Einstein-Tensor auf die gleiche Seite wie der Energie-Impuls-Tensor. Diese Umformung ist für jede beliebige Gleichung erlaubt.
0\space =\space k\space *\space T_{\mu\nu}\space -\space G_{\mu\nu}
Jetzt müssen sich die Raumzeitdichte und die Raumzeitkrümmung gegenseitig aufheben. Ein Vorzeichenwechsel für eine geometrische Abbildung ist immer ein Richtungswechsel. Damit zieht nun die Raumkrümmung von der Raumzeitdichte weg. Die Raumzeitdichte wird nun durch die Raumzeitkrümmung „auseinandergezogen“. Dies ist für die Raumzeit in Summe keine Veränderung, also gleich null.
Dazu holen wir uns nochmal die Abbildung 2-3. Das Bild gut einprägen, wir brauchen es noch öfters.

Wir sehen, dass die Raumzeitkrümmung die Raumzeit zur Raumzeitdichte hin verformt. Damit muss die Raumzeit außerhalb des Ringes in Richtung Raumzeitdichte verformt werden. Die Raumzeit ist ein Kontinuum und darf nicht „reißen“.
Verformt sich etwas in eine Richtung, dann muss der Nachbarbereich sich auch in diese Richtung verformen. Dann muss wieder der Nachbarbereich des Nachbarbereichs sich verformen usw. Daher muss die Raumzeitkrümmung eine unendliche Reichweite aufweisen.
Die Wirkung der Gravitation fällt mit der Entfernung ab. Diese muss stärker als linear abfallen. Mit der Entfernung, von einer Raumzeitdichte weg, kann die Raumzeitkrümmung auf ein immer größer werdendes Raumzeitvolumen zugreifen, dass sich mit verformen muss. Daher muss die Abschwächung in unserer 3D Raumzeit mit dem Abstandsquadrat erfolgen. In der entgegengesetzten Richtung der Gravitation (von der Raumzeitdichte weg) kommt auf eine Raumdimension 1D ein Zuwachs an Volumen um zwei Raumdimensionen dazu. Wenn wir den blauen Ring als Kugelschale in 3D betrachten, dann können wir immer weitere größere Kugelschalen um die Raumzeitdichte legen. Der Abstand r der Kugeloberfläche, auf welcher die Gravitation wirkt, wächst linear. Die Fläche selbst wächst aber mit r^2. Die Raumzeitkrümmung kann sich mit der Entfernung von Punkt zu Punkt zum Ausgleich einer immer größer werdenden Fläche bedienen. Damit muss diese wachsende Fläche immer weniger dagegen steuern und die Raumzeitkrümmung fällt mit r^2 ab.
Wir bleiben weiter bei der Abbildung 2-3. Wir können sehen, dass die Raumzeit zur Raumzeitdichte mit der Raumzeitkrümmung „nachschieben“ muss. Die Raumzeit muss hier ausgleichen. Dann macht für die Raumzeit nur Sinn, wenn das Nachschieben durch die Raumzeitkrümmung so gemacht wird, dass sich bis zur Gravitationsquelle hin die Raumzeitdichte der umgebenden Raumzeit durch die Raumzeitkrümmung nicht verändert. Die Raumzeitkrümmung muss daher eine Verformung der Raumzeit sein, welche selbst keine Veränderung der Raumzeitdichte erzeugt. Auch die „leere“ Raumzeit ohne ein Teilchen ist eine Raumzeit und hat daher eine Raumzeitdichte. Aus dem Ansatz mit der Raumzeitdichte heraus muss die Raumzeitkrümmung das bekannte Verhalten zeigen. Die Fläche der Raumzeit verändert sich nicht und die Raumzeitdichte bei der Raumzeitkrümmung verändert sich damit auch nicht.
Wir bleiben weiter bei der Abbildung 2-3. Wir können sehen, dass die Raumzeit zur Raumzeitdichte mit der Raumzeitkrümmung „nachschieben“ muss. Die Raumzeit muss hier ausgleichen. Richtig! Der Anfang wiederholt sich. Das ist kein Fehler. Die Aussagen brauchen wir hier nochmal.
Die Raumzeitkrümmung muss die Lücke zwischen Ring und Scheibe ausgleichen. Das bedeutet aber auch, dass die Raumzeitkrümmung explizit nicht in die Raumzeitdichte hinein ausgleichen darf. Für die Raumzeitkrümmung ist an der Grenze der Raumzeitdichte das Ende erreicht. In der Raumzeitdichte ist schon zu viel Raumzeit vorhanden. Da darf die Raumzeitkrümmung nicht hineinreichen und das Problem verschlimmern.
Wichtig! Die Raumzeitkrümmung ist nicht dazu da, die Raumzeitdichte auf null zu setzen. Diese muss auf Grund der Kontinuität der Raumzeit die fehlende Länge bis zur Raumzeitdichte hin ausgleichen. Die Raumzeitkrümmung soll die Raumzeitdichte nicht auflösen. Für die Raumzeitkrümmung ist nur die Menge an Raumzeitdichte interessant, da durch eine größere Raumzeitdichte eine größere Lücke ausgeglichen werden muss. Ob die Raumzeitdichte einen „inneren“ Aufbau besitzt, ist für die Raumzeitkrümmung und damit für die ART vollkommen egal. Die QM wird dann genau diesen „inneren“ Aufbau beschreiben.
Die Raumzeitkrümmung ist ein Ausgleich einer „Raumzeitlücke“, hervorgerufen durch die Raumzeitdichte. Die Raumzeitdichte selbst wird durch die Raumzeitkrümmung nicht verändert. Die Raumzeitkrümmung endet an der Grenze der Raumzeitdichte. Hier kann man schon erkennen, wie wir später die Singularität in der ART loswerden. Eine Raumzeitdichte ohne ein Raumzeitvolumen macht wenig Sinn. Kein Volumen, keine Dichte, keine Gravitation damit keine Singularität auf Grund der Gravitation. Wir werden die mathematische Abstraktion eines Punktes und damit die Singularität im Kapitel 3 „Grenzen der Raumzeit“ ausführlich besprechen.
Wir bleiben weiter bei der Abbildung 2-3. Wir können sehen, dass die Raumzeit zur Raumzeitdichte mit der Raumzeitkrümmung „nachschieben“ muss. Die Raumzeit muss hier ausgleichen. Ja, nochmal!
Was wir auch noch erkennen können, ist, dass sich die Raumzeit im Kreis durch höhere Raumzeitdichte, auf die Scheibe verdichtet hat. Die Raumzeitdichte in der Scheibe ist für die ART egal. Die Menge an Raumzeitdichte bestimmt die Größe der Scheibe und dies interessiert die Raumzeitkrümmung. Damit kann die Raumzeitdichte in der Scheibe gleichverteilt angenommen werden. Die Beschreibung der Raumzeitdichte kann dadurch in einer linearen Beschreibung erfolgen. Das wird einer der Gründe werden, warum man die QM linear beschreiben kann.
Bei der ART ist dies nicht der Fall. Die Raumzeitkrümmung verändert bei sich selbst die Raumzeitdichte nicht. Wie wir aber sehen, „schiebt“ die Raumzeit durch Raumzeitkrümmung weitere Raumzeit zur Raumzeitdichte hin nach. Das bedeutet, dass sich durch die Raumzeitkrümmung im Kreis die Raumzeitdichte wieder etwas erhöht hat. Damit haben wir einen selbstverstärkenden Effekt. Die mathematische Beschreibung der ART darf auf keinen Fall linear ausfallen.
Der Wunsch aller Physiker ist, dass sich bei einer Vereinigung der ART mit der QM, aus einem Ansatz der QM heraus, die ART evtl. auch linear beschreiben lässt. Lineare Beschreibungen lassen sich einfacher lösen. Bei der QM ist die Beschreibung linear aber von Grund auf extrem kompliziert. Nur weil dies eine lineare Beschreibung ist, lässt sich darin überhaupt irgendetwas berechnen. Die Beschreibung der ART ist nicht so kompliziert und mathematisch sehr gut verstanden. Die ART ist aber leider nicht linear. Somit sind in beiden Bereichen die Supercomputer damit beschäftigt Näherungslösungen zu berechnen.
Zum Abschluss wählen wir noch ein Thema aus, dass nicht zur ART gehört. Wir wollen sehen, dass der Ansatz mit Raumzeitdichte auch in anderen Bereichen der Physik trägt. Dafür wählen wir etwas aus, dass es in vielen verschiedenen Formen gibt. Wir wollen ein großes Spektrum abdecken. Zusätzlich wählen wir etwas aus, wo niemand ein Problem sieht. Die Sichtweise in der Physik soll sich grundlegend ändern. Damit sind auch Bereiche gemeint, die man vermeintlich als „Verstanden“ abgehackt hat. Die Wahl ist auf die Bindungsenergie gefallen.
Die Bindungsenergie gibt es im Atomkern, der Atomhülle, zwischen Atomen oder Molekülen. Sogar die Abgabe von Energie, bei der Verschmelzung von zwei Schwarzen Löchern, kann nach diesem Schema erklärt werden. Das Gesamtgebilde hat zusammen weniger Energie als die Einzelteile vor der Bindung. Wir nehmen hier als Beispiel die Fusion von Wasserstoff zu Helium. Es gibt mehrere Prozesse in der Sonne, wie sich Wasserstoff zu Helium verwandelt. Wir vereinfachen den Prozess sehr stark. Das ist für unsere Zwecke ausreichend.
Wir gehen davon aus, dass sich Wasserstoff H_1 in Wasserstoff H_3 verwandelt und dieser dann zu Helium H_4 fusioniert. Dabei interessiert uns eigentlich nur das Endergebnis, der Heliumkern.
Die QM rechnet uns exakt aus, mit welcher Wahrscheinlichkeit diese Fusion stattfindet und welche Energie dabei freigesetzt werden muss. In welcher Form die Energie abgegeben wird ist hier nicht relevant. Wir starten unser Fragespiel: Warum? Dann erhält man oft zwei Antworten.
Leider sind dies keine Antworten auf die Frage. Warum ein stabile Energieniveaus, Entropie? Das Fragespiel kann man hier lange betreiben. Für uns wichtig:
Mathematik ist für die Physik eine konsistente Beschreibung der Natur durch ein passendes Modell. Mit diesem Modell können wir Untersuchungen machen und Vermutungen anstellen. Die Mathematik wird aber niemals in der realen Natur etwas erzeugen oder erzwingen! Das Warum muss diese Frage klären und die Modellbeschreibung kann dann ein passendes Wie dazugeben.
Wie wollen wir dies mit Raumzeitdichte erklären. Die zwei H_3 Bausteine müssen für eine Bindung eine räumliche Nähe haben. Bindung funktioniert nur bei einer räumlichen Nähe. In diesen Fall müssen sich die zwei Bausteine so nahekommen, dass die starke Kernkraft eine Wirkung erzeugen kann. Der genaue Ablauf welche Nukleonen miteinander reagieren dürfen, klären wir später in der QM.
Hier geht es darum, dass im Endergebnis 2 Protonen und 2 Neutronen einen Heliumkern bilden. Für die Darstellung nimmt man in den Lehrbüchern oft eine Kugel je Nukleon. Das versuchen wir hier auch. Das ein Proton oder ein Neutron selbst wieder zusammengesetzte Systeme sind blenden wir hier aus.
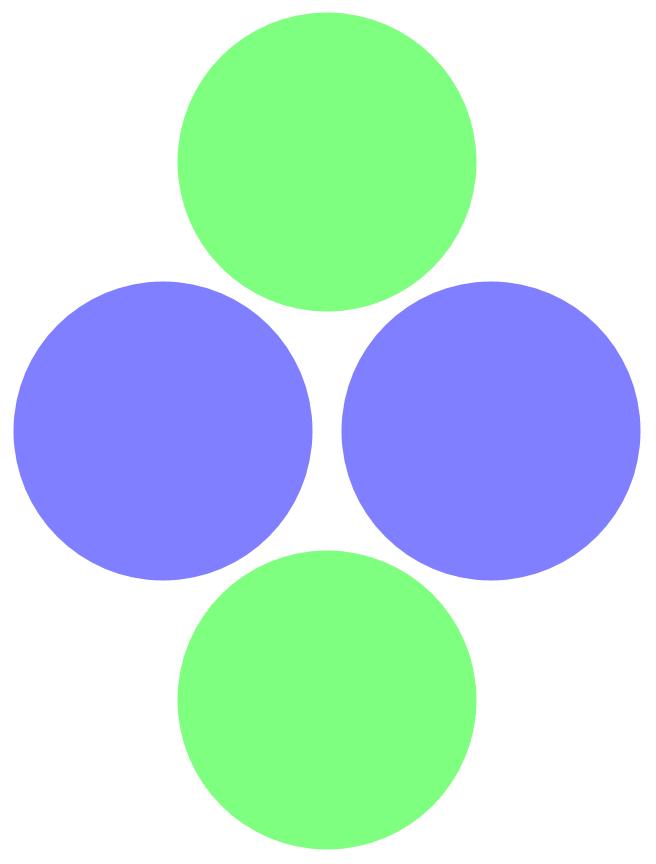
Jetzt wissen wir, dass der Heliumkern so auf keinen Fall aussieht. Experimente haben ergeben, dass ein Atomkern eher wie eine einzige Kugel mit Ausbeulungen aussehen muss. Die Berechnungen der QM bestätigt dies. Wie kommen wir von 4 einzelne Nukleonen auf eine Kugel, welche nicht sehr viel größer sein soll als die einzelnen Nukleonen? Zum Glück haben wir unsere Raumzeitdichte.
Eine Raumzeitdichte ist kein Gebilde mit einer abgeschlossenen Grenze. Alles ist Raumzeit. Damit können sich einzelne Raumzeitdichte überlagern. Daher funktionieren Bindungen immer nur ab einer gewissen räumlichen Nähe. Für uns sieht der Heliumkern eher so aus.
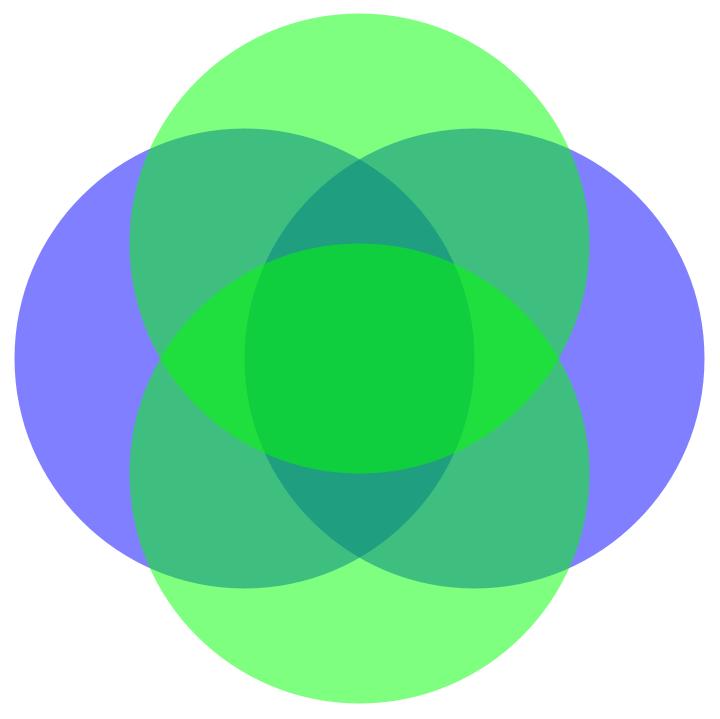
Die einzelnen Nukleonen sind eine Raumzeitdichte. Eine Raumzeitdichte kann sich überlagern. Jedes einzelne Nukleon hat mit der Überlagerung zu viel Raumzeitdichte, um ein Proton oder Neutron zu sein. Damit die Nukleonen auf ihrem Niveau der Raumzeitdichte bleiben können, muss ein Teil der Raumzeitdichte weg. Es ist zu viel da! Die Nukleonen wollen nicht auf ein niedrigeres Energieniveau. Die Nukleonen müssen auf ihrem festgelegten Energieniveau bleiben. Wollen wir diesen Kern in seine Bestandteile zerlegen, so müssen wir die fehlende Raumzeitdichte wieder zuführen. Damit erklärt der Ansatz mit einer Raumzeitdichte die Bindungsenergie sehr einfach. Zur Bindungsenergie gibt es eine kleine Übersicht.
Wie wir sehen können, steigt die Bindungsenergie bei wenigen Nukleonen sehr stark an. Das macht Sinn, da an Anfang mit jedem einzelnen Nukleon eine neue große Schnittmenge der Raumzeitdichte erzeugt wird. Je mehr Nukleonen bereits im Atomkern vorhanden sind, umso geringer fällt die neue Schnittmenge zwischen den Raumzeitdichten aus.
Bei einer bestimmten Anzahl an Nukleonen kann die Bindungsenergie wieder abfallen. Die Abstoßung durch die Ladung sorgt dafür, dass sich die Nukleonen nicht beliebig überlagern können. Daher kann es durch die Geometrie der Überlagerung auch weniger Bindungsenergie geben, wenn ein neues Nukleon dazukommt. Bei Eisen Fe_{56} ist dann Schluss. Jedes neue Nukleon verursacht durch die Veränderung der Schnittmengen zwischen den Raumzeitdichten eine geringere Schnittmenge.
Zusätzlich gibt es sogenannte „magische Zahlen“ 2, 8, 20, 28, 50 und 82. Diese Anzahl an Nukleonen scheint eine sehr stabile Bindung zu haben. Laut QFT ergibt sich, bei der „Deformation“ des Atomkerns, bei diesen Zahlen eine fast exakte Kugel, für den gesamten Atomkern. Eine glatte Kugel als Ganzes hat die höchstmögliche Schnittmenge der Nukleonen.
Wie wir sehen, können wir mit dem Ansatz einer Raumzeitdichte auch in Bereichen außerhalb der ART das Warum erklären. Damit schließen wir dieses Kapitel und schauen uns die wichtigste Schlussfolgerung aus der Raumzeitdichte an.
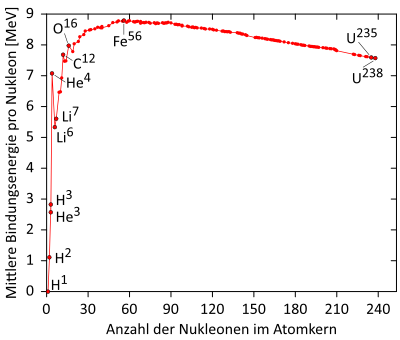
Wie wir sehen können, steigt die Bindungsenergie bei wenigen Nukleonen sehr stark an. Das macht Sinn, da an Anfang mit jedem einzelnen Nukleon eine neue große Schnittmenge der Raumzeitdichte erzeugt wird. Je mehr Nukleonen bereits im Atomkern vorhanden sind, umso geringer fällt die neue Schnittmenge zwischen den Raumzeitdichten aus.
Bei einer bestimmten Anzahl an Nukleonen kann die Bindungsenergie wieder abfallen. Die Abstoßung durch die Ladung sorgt dafür, dass sich die Nukleonen nicht beliebig überlagern können. Daher kann es durch die Geometrie der Überlagerung auch weniger Bindungsenergie geben, wenn ein neues Nukleon dazukommt. Bei Eisen F_{56} ist dann Schluss. Jedes neue Nukleon verursacht durch die Veränderung der Schnittmengen zwischen den Raumzeitdichten eine geringere Schnittmenge.
Zusätzlich gibt es sogenannte „magische Zahlen“ 2, 8, 20, 28, 50 und 82. Diese Anzahl an Nukleonen scheint eine sehr stabile Bindung zu haben. Laut QM ergibt sich, bei der „Deformation“ des Atomkerns, bei diesen Zahlen eine fast exakte Kugel, für den gesamten Atomkern. Eine glatte Kugel als Ganzes hat die höchstmögliche Schnittmenge der Nukleonen.
Wie wir sehen, können wir mit dem Ansatz einer Raumzeitdichte auch in Bereichen außerhalb der ART das Warum erklären. Damit schließen wir dieses Kapitel und schauen uns im nächsten Kapitel die wichtigste Schlussfolgerung aus der Raumzeitdichte an, eine Raumzeit besitzt Grenzen. In diesem neuen Kapitel wird die Raumzeitdichte mit der Idee der Raumzeitgrenze weiter definiert. Damit sind wir noch nicht fertig.