
Everything consists of spacetime.
Die ART basiert auf nur 3 Prinzipien
Das Relativitätsprinzip und die Lichtgeschwindigkeit haben wir schon im Kapitel zur SRT hergeleitet. Für die ART fehlt noch das Äquivalenzprinzip. Davon gibt es gleich zwei Stück. Das schwache und das starke Äquivalenzprinzip. Wir werden beide separat behandeln. Das starke ist ausreichend, da es das schwach beinhaltet. Deshalb die gewählten Namen. Die getrennte Herleitung ist für den logischen Aufbau interessant. Das erstaunliche Ergebnis aus der Herleitung ist, dass die Raumzeit selbst ein Potentialfeld ist. Dies wird nochmals in der Kosmologie, in einer anderen Form, sehr wichtig. In der ART ist das vektorielle Potentialfeld der Raumzeit identisch mit dem Potentialfeld der Gravitation. Alle anderen Potentialfelder in der Physik funktionieren nach dem gleichen Prinzip. In der QM in jeweils unterschiedlichen Raumzeitkonfigurationen.
Zusätzlich werden wir in diesem Kapitel klären, was eine Kraft in der klassischen Beschreibung der Physik ist. Das hilft beim Verständnis der Gravitation. Gerade der geniale Gedanke von Einstein, eine Kraft als geometrischen Abbildung in der Raumzeit, ist nicht immer sofort verständlich. Wir erkennen dann leichter, warum wir so unterschiedliche Beschreibungen für ein identisches Phänomen verwenden können.
Fangen wir schwach an, dann können wir uns steigern. Das schwache Äquivalenzprinzip ist bereits in der guten alten Mechanik von Newton enthalten. In der klassischen Mechanik war allerdings unklar, warum dies so ist. Hier wird das Prinzip oft als die Gleichheit von träge und schwere Masse bezeichnet.
Was für Einstein E\space =\space mc^2 ist, ist für Newton F\space =\space ma. Die zwei bekanntesten Formeln der Welt. Kraft gleich Masse mal Beschleunigung. Das zweite Newtonsche Axiom. Die Masse m in der Formel ist die träge Masse. Träge, da diese ihren Bewegungszustand nicht verändert, wenn keine Beschleunigung auf ihr wirkt. Je mehr Masse vorhanden ist, umso größer muss die Beschleunigung sein, die wir für eine identische Veränderung aufbringen müssen. Keine Beschleunigung keine Kraft und damit keine Veränderung => Trägheit. Da in der Formel die Masse das einzige Objekt ist, muss diese Trägheit mit der Masse verbunden sein. Soweit alles sehr einfach.
Gleiche Frage wie bei der SRT. Warum gibt es dann das erste Axiom? Na, wisst Ihr es noch auswendig? Ich helfe nach: „Ein kräftefreier Körper bleibt in Ruhe oder bewegt sich geradlinig und gleichförmig“. Das hatten wir bereits im zweiten Axiom. Keine Beschleunigung, keine Veränderung. Wieso gibt es diese Aussage zweimal in getrennten Axiomen? Hier eine Argumentation ohne das Relativitätsprinzip. Damit dies einen Sinn ergibt, müssen wir das erste Axiom anders lesen. Wir drehen die Aussage um: Wenn auf einen Körper keine Kräfte wirken, dann ist das, was der Körper macht Ruhe oder eine gradlinige und gleichförmige Bewegung.
Das erste Axiom ist auch eine Messvorschrift. Wir können messen, was eine gerade und gleichförmige Bewegung ist. In einer Raumzeit mit Raumzeitkrümmung ist „gerade“ nicht so einfach festzustellen. Damit wird eine beliebte Aussage, zur Gravitation fragwürdig. Ein Körper in einem Gravitationsfeld fällt kräftefrei auf einer geraden Linie zum Gravitationszentrum. Wir werden sehen, dass diese Aussage mit Vorsicht zu genießen ist. Hier werden wir den Unterschied von Potenzialfeld und Kraft kennen lernen.
Die nächste berühmte Formel von Newton ist die Formel zu Gravitationskraft
F\space =\space \cfrac{G\space *\space M_{schwer}\space *\space m_{schwer}}{r^2}
Das große M soll bei uns die Erde sein und das kleine m eine Testmasse. Die Masse hier ist die schwere Masse. Das, was die Waage anzeigt. Diese Formel stellen wir anders zusammen.
F\space =\space \cfrac{G\space *\space M_{schwer}}{r^2}\space *\space m_{schwer}
Der erste Term mit dem Bruch ist laut den Maßeinheiten eine Beschleunigung. Für die Erde als M kommt hier das bekannt kleine g für die Erdbeschleunigung heraus. Das ergibt:
m_{träge}\space *\space a\space =\space g\space *\space m_{schwer}
Wenn hier irgendetwas zusammenpassen soll, dann müssen wir die verschiedenen m oder g und a wegkürzen können. Das bringt uns zu den folgenden Aussagen:
Die Identität von träge und schwere Masse war bei Newton ein Rätsel. Wir sehen, es muss so sein, aber es gab keinen Grund dafür. Diese Identität ist zurzeit, im Jahr 2026, sehr genau überprüft. Eine Abweichung kann es erst nach der 14ten Stelle hinter dem Komma geben. Mit einer der am besten überprüfte Werte überhaupt.
Die Identität von träge und schwere Masse war bei Newton ein Rätsel. Wir sehen, es muss so sein, aber es gab keinen Grund dafür. Diese Identität ist zurzeit, im Jahr 2026, sehr genau überprüft. Eine Abweichung kann es erst nach der 14ten Stelle hinter dem Komma geben. Mit einer der am besten überprüfte Werte überhaupt.
Wird jemals ein Unterschied festgestellt, egal wie weit hinter dem Komma, ist die DP falsifiziert.
Irgendwie muss es eine Verbindung von Kraft und Gravitation als geometrische Abbildung geben. Das starke Äquivalenzprinzip bezieht sich auf eine Beschleunigung. Diese erzeugt in der klassischen Mechanik immer eine Kraft. Die Lösung ist bereits bei den Axiomen von Newton enthalten. Erstes und zweites Axiom: Eine Kraft ist eine Veränderung.
Wir können in der DP die klassische Kraft als eine Veränderung der Raumzeitdichte auffassen. Ohne eine Wechselwirkung bleibt eine Raumzeitdichte, was diese ist. Über eine Wechselwirkung kann sich diese verändern. Das ist sehr einfach. Wir haben aber speziell bei der Gravitation ein großes Problem. Was wird in einer Wechselwirkung ausgetauscht? Das lange gesuchte Graviton als Austauschteilchen der Quantengravitation? Nein, ganz bestimmt nicht!
In der ART gibt es nur eine geometrische Abbildung als Raumzeitkrümmung für die Gravitation. Alle Masse-Energie-Äquivalente sind im Energie-Impuls Tensor gesammelt. Im Einstein Tensor haben wir keine Raumzeitdichte als Austauschteilchen. Wir benötigen aber trotzdem eine Veränderung auf einer Raumzeitdichte. Genau hier liegt die Stärke der DP. Wir haben eine Krümmung oder eine Dichte, mehr ist nicht da. Eine Dichte kann es nicht sein. Es bleibt nur noch eine einzige Möglichkeit übrig. Die Raumzeitkrümmung muss eine Veränderung an der Raumzeitdichte bewirken ohne ein Austauschteilchen und ohne eine Veränderung an der Raumzeitdichte. Ich weiß, der Satz klingt etwas bescheuert. Ist aber genau so gemeint.
Letztendlich müssen wir auf das starke Äquivalenzprinzip kommen. Dort darf die Gravitation von einer Beschleunigung, in der Wirkung auf eine Masse, nicht unterscheidbar sein. Damit muss die Raumzeitkrümmung einer Veränderung an der Raumzeitdichte erzeugen, die einer Beschleunigung entspricht. Auf die DP hätte man auch schließen können, wenn man den Begriff eines Potentials und hier des Gravitationspotentials vollständig erklären will. Leider war man bereits mit der exakten Berechnung zufrieden. Das Warum war nicht mehr interessant.
Kraft ist für uns eine Veränderung der Raumzeitdichte. Da die Raumzeitdichte auch ein Bewegungszustand ist, sollte es nicht verwundern, dass mit der Kraft eine Beschleunigung verbunden ist. Die Veränderung eines Bewegungszustands benötigt eine Beschleunigung. Damit ist der Begriff Kraft geklärt. Gehen wir weiter und schauen uns endlich das starke Äquivalenzprinzip an.
Im starken Äquivalenzprinzip können wir die Wirkung der Gravitation von der Wirkung einer Beschleunigung nicht unterscheiden. Gravitation und Beschleunigung müssen nicht identisch sein, wir dürfen nur nicht die Wirkung unterscheiden können.
Den ersten Ansatz haben wir im schwachen Äquivalenzprinzip gesehen. Dort mussten a und g identisch sein. Einstein ist dann auf die Idee gekommen, dass eine Bewegung in einem gekrümmten Raum genau dieser Beschleunigung entsprechen muss. Wie wir an dem Wort „Wirkung“ erkennen können, war Ihm bereits klar, dass dies mit unterschiedlichen Phänomenen verwirklicht wird.
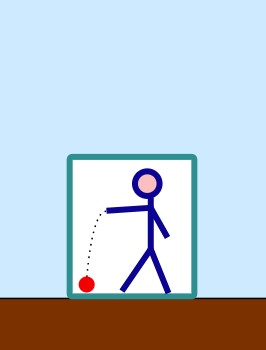

Wir sind wieder mit der abgeschlossenen Kiste von Galileo unterwegs. Bei der SRT war es ohne eine Wirkung von außen. Hier ist es die Gravitation oder die Beschleunigung der Rakete. In den beiden Kisten können wir mit keinem Experiment feststellen, ob es Gravitation oder Beschleunigung ist. Die Wirkung ist identisch.
Da man am Anfang der ART mit einer Verformung der Raumzeit noch nicht viel anfangen konnte, hat man sich an der alten Analogie mit der Beschleunigung gehalten. Damit wir eine Wirkung wie eine Beschleunigung erhalten, muss das Testobjekt m in der gekrümmten Raumzeit in das Gravitationszentrum „fallen“. Ich glaube, dass dies Analogie die Suche nach der Warum-Frage ausgebremst hat. Der Mond fällt zur Erde. Da die Raumzeit gekrümmt ist fällt der Mond auf seiner Umlaufbahn um die Erde. Berechnen lässt sich dies auch sehr gut. Das kann jeder verstehen und alle sind zufrieden.
Wir nicht! Diese Analogie erklärt gar nichts. Laut der Berechnung in der ART bewegt sich der Mond auf einer Geodäte um die Erde. Dieser Begriff bezeichnet die Bewegungsrichtung ohne eine Einwirkung einer Kraft. In einer Raumzeit ohne Gravitation ist dies eine Gerade. Mit Gravitation dann die fast kreisrunde Bahn um die Erde. Kräftefrei, dass erinnert uns doch an das erste Newtonsche Axiom. In einer flachen Raumzeit gerade und gleichförmig. In einer gekrümmten Raumzeit eben immer der Krümmung hinterher. Das ist aber genau die Messvorschrift, welche besagt, der Mond unterliegt keiner Wechselwirkung. Keine Beschleunigung und damit keine Veränderung. Wo soll da eine Wirkung als Beschleunigung herkommen? Das erste Axiom und das zweite Axiom schließen sich bei einer Beschleunigung gegenseitig aus. In der ART wird aber so getan, als ob man beides gleichzeitig haben kann. Der kräftefreie Mond (da auf Geodäte) fällt (und damit beschleunigt) um die Erde. Nein, so geht es nicht.
So, wieder etwas beruhigen und weiter geht es. Keine Wechselwirkung von außen und wir brauchen trotzdem eine Veränderung. Diese Veränderung bleibt, zum Beispiel beim Mond, über Milliarden von Jahren hinweg konstant. Diese Frage ist nie gelöst worden. Also machen wir das jetzt.
Die erste Idee, die wir haben können, ist, dass sich der Wert der Raumzeitdichte in einer Raumzeitkrümmung verändert. Dann haben wir von außen keine Wechselwirkung und trotzdem einen veränderten Wert. Das klingt schon sehr gut nach der gesuchten Lösung. In der Raumzeitkrümmung wird die Länge immer größer und die Länge der Raumzeitdichte bleibt gleich. Dann wird im Verhältnis die Dichte doch immer größer. Damit erhält die Raumzeitdichte durch die Umgebung eine immerwährende Veränderung = Beschleunigung. Ja schon, aber wir haben eine Raumzeit. Bei der Zeitdimension verhält es sich genau umgekehrt und alles gleicht sich wieder aus.
Nicht traurig sein, das ist gut so. Wir brauchen eine Energieerhaltung. Die Raumzeitkrümmung verändert für ihren Bereich die Raumzeitdichte nicht. Ihr erinnert euch an dem gleichbleibenden Flächeninhalt. Damit verändert sich auch das Verhältnis einer Raumzeitdichte zur umgebenden Raumzeit mit Raumzeitkrümmung nicht.
Letztendlich haben wir von außen keine Wechselwirkung. Damit kann sich das Verhältnis der Raumzeitdichten von Umgebung und Objekt nicht verändern. Wir haben aber nur Raumzeitkrümmung und Raumzeitdichte, wo kann es dann noch herkommen?
Das Einzige, was jetzt noch übrig bleibt sind die Verschiebungen zwischen Raumdimension und Zeitdimension bei der Raumzeitkrümmung. Schauen wir uns das genauer an.
Eine Raumzeitdichte bewegt sich mit 1 m/s auf die Erde zu. Weit weg von der Erde ist dies eine gradlinige und gleichförmige Bewegung. Hier nochmals der wichtige Hinweis: Raumzeitdichte ist auch immer der Bewegungszustand. Da wir keine Wechselwirkung von außen haben, muss die Geschwindigkeit auch so bleiben. Keine Veränderung der Raumzeitdichte ist identisch zu gleichem Bewegungszustand. In der Raumzeitkrümmung verändern aber Raum und Zeit ihre Definition. Der Meter wird länger und die Sekunde wird langsamer. Das passiert aber nur für die umliegende Raumzeit und nicht für die Raumzeitdichte. Die Geschwindigkeit muss bei 1 m/s bleiben. Damit muss die Raumzeitdichte schneller werden. Diese muss nun eine längere Strecke mit weniger Zeit überbrücken. Die Raumzeitdichte wird beschleunigt, nur auf Grund der gegenläufigen Veränderung der Raum- und Zeitdimensionen. Lokal ist die Raumzeitdichte frei von jeder Kraft, da diese sich nicht verändert. Diese etwas seltsame Beschleunigung ist genau, was wir brauchen:
Das starke Äquivalenzprinzip ergibt sich aus den gegenläufigen Verformungen der Raumzeitkomponenten in einer Raumzeitkrümmung. Die Raumzeitdichte erfährt explizit keine Veränderung oder Wechselwirkung. Wir erhalten eine Beschleunigung, weil sich der Bewegungszustand nicht verändern darf. Das ist der Witz an dem Äquivalenzprinzip nach der DP. Hier erkennen wir wieder, wie wichtig es ist, dass diese Verformung eine Veränderung der Definition und nicht nur eine Sichtweise ist. Das Äquivalenzprinzip funktioniert nur bei einer Veränderung der Definition.
Die Veränderung der Raumzeitkomponenten kann auch den gegenteiligen Effekt haben. Das passiert genau dann, wenn man per Beschleunigung die Geschwindigkeit gar nicht mehr erhöhen kann. Wir müssen den Sonderfall der Lichtgeschwindigkeit betrachten. Da haben wir zwei Möglichkeiten:
Da zu schauen wir uns folgendes Bild an:
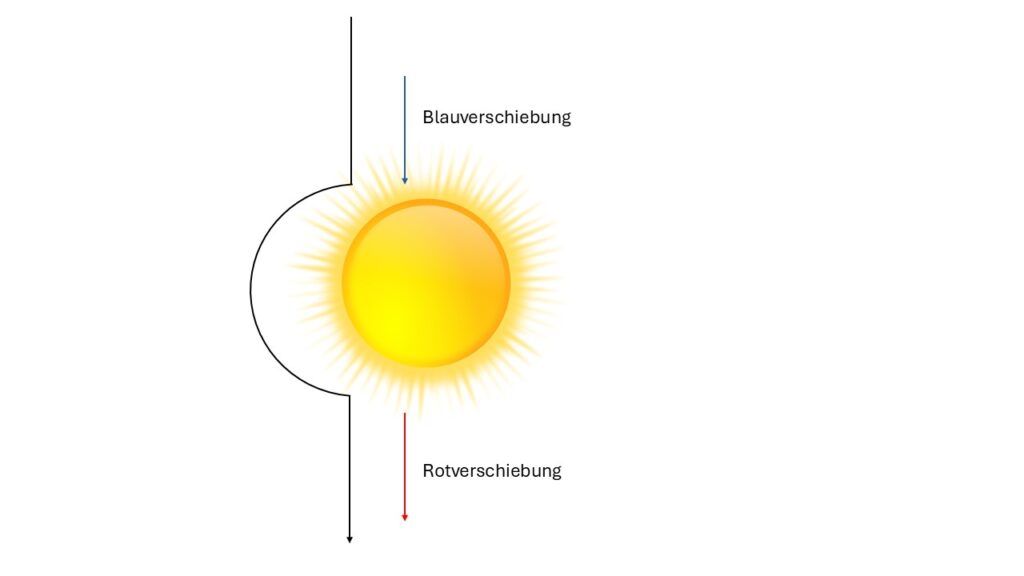
Ein Photon mit Lichtgeschwindigkeit fliegt sehr knapp an der Sonne vorbei. Während das Photon auf die Sonne zufliegt, wird es blauverschoben. Wen es von der Sonne wegfliegt, im gleichen Maße Rotverschoben. Da gibt es in Summe keine Veränderung der Frequenz.
Das Photon muss aber der Raumkrümmung folgen. Diese ergibt für das Photon einen längeren Weg. Dann muss doch einfach der längere Weg mit Lichtgeschwindigkeit durchflogen werden und alles ist perfekt. So hatte man sich dies auch gedacht, bis Herr Shapiro, für Licht in der Mathematik der ART, eine Abweichung entdeckt hat. Lichtsignale müssen beim Vorbeiflug an einer Masse eine geringere Geschwindigkeit aufweisen. Der Effekt ist auf ca. 4 Stellen hinter dem Komma experimentell bestätigt
Selbst auf die Gefahr hin, dass es euch zum Halse raushängt. Auch hier sehen wir beim Äquivalenzprinzip, dass die Veränderung der Raumzeitmetrik zwingend eine Veränderung der Definition der Geometrie sein muss. Wäre diese Krümmung nur eine längere Wegstrecke, dann würde sich dieser Effekt nicht einstellen.
Das Photon hat die maximale Geschwindigkeit. In der Raumzeitkrümmung wird per Definition der Weg länger und die Zeit kürzer. Beschleunigen geht nicht. Das Photon wird in dieser Umgebung für einen Beobachter langsamer. Lokal behält das Photon die Lichtgeschwindigkeit, das hatten wir bei der SRT besprochen.
Tatsächlich ist auch schon Einstein auf eine Verzögerung gestoßen. Aber erst Herr Shapiro hatte dann das richtige Ergebnis. Bei Einstein fehlte noch eine 2 in der Formel. Die ist aber wichtig. Wir haben eine längere Strecke und eine verlangsamte Zeit. Daher ist die Verzögerung gedoppelt.
Gibt es denn zur Gravitation auch die Anti-Gravitation. Wie das + und – bei der elektrischen Kraft. Bei der Gravitation ist immer alles nur anziehend. Laut der ART, ja. Das war ein sehr überraschendes Ergebnis aus der Mathematik der ART heraus. Die Gravitation wirkt abstoßend, wenn diese zu stark wird. Bei der Mathematik ist dies möglich, da die ART keine lineare Gleichung ist. Nur mit reiner Logik ist das eher schwer zu begreifen.
Dabei ist nicht die Aufhebung der Gravitation durch die Geometrie des Objektes gemeint. Der Mittelpunkt einer Hohlkugel ist ohne Gravitation, obwohl man von Masse umgeben ist. Da die Gravitationskraft eine vektorielle Kraft ist, hebt sich diese in einem Mittelpunkt auf. Wenn wir für die Lösung der Feldgleichung nicht die Schwarzschild-Metrik, sondern die Kerr-Metrik benutzen, dann passiert dies auch im Zentrum eines Schwarzen Loches. Die Singularität ist dann nicht ein Punkt, sondern ein Ring im Zentrum eines Schwarzen Loches. Das kommt daher, dass da die Kerr-Metrik ein rotierendes Schwarzes Loch abbilden kann. Damit ist das auch die exaktere Lösung. Durch die Rotation wird aus der Singularität kein Punkt, sondern ein Ring. Im Zentrum des Ringes ist die Schwerkraft null. Die Gravitation zur Singularität hebt sich auf.
Was wir haben wollen, ist eine abstoßende Wirkung, nicht eine Aufhebung. Diese Abstoßung gibt es laut ART im Zentrum eines Schwarzen Loches, bei sehr großer Gravitation. Daher komme auch immer wieder Ideen, wie unser Universum ist der Mittelpunkt eines gigantischen Schwarzen Loches. Da dies die Mathematik so angibt, wird es einfach angenommen.
Wie steht den die DP dazu. Da wir die Mathematik der ART, bis auf die Singularität, bestätigen wollen, sollte es sowas auch geben. Genau das passiert auch. Mit einem entscheidenden Unterschied. Wir können mal wieder den Grund für diese „Abstoßung“ sauber erklären. Diese Abstoßung brauchen wir in der DP auch nur bei sehr hoher Gravitation oder besser ausgedrückt bei sehr hoher Raumzeitdichte.
Raumzeitkrümmung ist die Reaktion auf Raumzeitdichte. Dabei wird die Raumdimension länger und die Zeitdimension kürzer. Für eine Anti-Gravitation müssen wir dies umkehren. Die Raumdimension muss kürzer und die Zeitdimension länger werden. Das passiert aus zwei Gründen:
Raumzeit ist ein Kontinuum. Damit gibt es zwischen der Raumzeitdichte und der Raumzeitkrümmung keine Grenze. Das geht direkt ineinander über. Das ist kein Problem, solange der Unterschied von der Raumzeitdichte zur Raumzeitkrümmung nicht zu große ist. Das Problem erscheint, wenn wir von einer extremen Raumzeitdichte zu einer extremen Raumzeitkrümmung übergehen wollen. Für die Zeitdimension haben wir kein Problem. In beiden Fällen wir die Zeitdimension kürzer und wir haben damit bereits einen passenden Übergang. Bei der Raumdimension ist es anders. Die wird bei der Raumzeitdichte kleiner und bei der Raumzeitkrümmung größer. Ab einem bestimmten Unterschied zwischen diesen Verhalten, ist die Differenz größer als unsere Dimensionale Konstante d die Veränderung innerhalb einer bestimmten Länge zulässt. Das funktioniert so nicht. Zwischen der Raumzeitdichte und der Raumzeitkrümmung muss dann einen Bereich geben, wo sich dies kontinuierlich anpasst. Wir bekommen aus der Raumzeitkrümmung bis zur Raumzeitdichte ein Anti-Gravitation. Die Raumdimension wird kleiner und nicht länger. Da auch die Zeitdimension sich anpassen muss, aber eigentlich schon das passende Verhalten hat, geht auch diese Anpassung nur innerhalb einer bestimmten Länge.
Wir erhalten eine Anti-Gravitation kurz vor der „Singularität“. Das ist das gewünschte Verhalten laut der Feldgleichung und wir wissen jetzt auch, warum dies so ist. Dies passiert aber nur, wenn wir in die Nähe von d kommen. Je größer die Raumzeitdichte, umso größer wird der Bereich des Übergangs mit der Anti-Gravitation. In unserem Sonnensystem werden wir keine Anti-Gravitation feststellen können.
Der Schlussakt für dieses Kapitel soll das Gravitationspotential sein. Aus meiner Sicht ist die Bezeichnung Potential einer der am wenigsten verstandenen aber zur Berechnung am häufigsten benutzen Begriffe der Physik. Wenn es nicht 100% exakt sein muss, dann rechnet wir bei einem Problem mit der Gravitation immer mit dem Potential und nicht direkt mit der Raumzeitkrümmung. Das ist sonst viel zu kompliziert. Die Flugbahnen fast alle Körper, die wir in den Weltraum geschossen haben und noch in Zukunft hochschießen werden, wurden so berechnet.
Wenn wir einen Physiker fragen, was ist ein Potential? Kommt fast immer etwas in der Richtung: Das Potential ist die Fähigkeit die potenzielle Energie in Bewegungsenergie umwandeln zu können. Ok, woher kommt diese Fähigkeit, steckt diese im Körper? Da sind sich alle einige, dass diese Fähigkeit im Potential und nicht im Körper steckt. Der identische Körper außerhalb eines Potentials erfährt keine Beschleunigung. Was ist dann diese Fähigkeit? Meist stellt sich dann Ruhe ein. Oft kommt die Antwort: Eine Eigenschaft des Potentials. Wir sind wieder am Anfang.
Bei fast allen Potentialen, ist es wichtig, ob der Testkörper überhaupt an der Wechselwirkung des Potentials teilnimmt. Ein neutrales Neutrino ist von einem elektrischen Potential vollkommen unbeeindruckt. Bei der Gravitation haben wir die Besonderheit, dass absolut alles, was wir als Objekt identifizieren können, bei dem Gravitationspotential mitmacht. Das macht Sinn, da in der DP alles eine Raumzeitdichte in der gekrümmten Raumzeit ist und damit mitmachen muss. Bei den anderen Wechselwirkungen gibt die Geometrie in der QM an, ob eine Wechselwirkung stattfinden darf.
Wir haben noch eine Besonderheit. Der „interne Aufbau“ des Objektes mit der passenden Ladung für das Potential spielt keine Rolle. Ob ein Elektron als Elementarteilchen mit der Elementarladung von 1 oder ein fast 2000-fach schwereres zusammengesetztes Proton mit der Elementarladung 1 mitmacht, spielt für die Wirkung keine Rolle. Es geht nur um die Elementarladung von 1. Bei der Gravitation, machen aber auch Teilchen mit, die keine Ladung, hier keine Masse, haben, z.B. das Photon. Es geht um die Abweichung von Längendimension zur Zeitdimension. Diese ist bei der Raumzeitdichte immer null, da die Raum- und die Zeitdimension sich identisch verformen. Die Abweichung kommt nur und ausschließlich aus der Umgebung mit Raumzeitkrümmung. Das wird bei den anderen Potentialen, wie das Elektrische Feld auch so sein.
Wollen wir aus dem Gravitationspotential wieder raus, dann müssen wir gegen diese Beschleunigung antreten. Wir brauchen eine Rakete. Die Beschleunigung ist nicht nur ein Scheineffekt. Eine Rakete muss ordentlich Leistung bringen, um erfolgreich gegen diese Beschleunigung arbeiten zu können. Dieses Mal bringen wir per Wechselwirkung eine Kraft mit der Rakete auf und damit wird die Raumzeitdichte tatsächlich erhöhen. Der Bewegungszustand der Raumzeitdichte (Rakete) und damit die Energie selbst, muss durch Beschleunigung auf Fluchtgeschwindigkeit erhöht werden.
Durch die Beschleunigung wird die Bewegungsenergie in potenzielle Energie umgewandelt. So lautet die klassische Aussage zu einem Gravitationspotential. Tatsächlich wird da nichts in eine potenzielle Energie umgewandelt. Die Rakete muss die Beschleunigung gegen die Gravitation real durch eine Wechselwirkung erzeugen. Die Rakete kommt aus dem Gravitationspotential heraus und hat dann einen höheren Bewegungszustand außerhalb des Potentials.
Das Rechnen mit dem Potential ist sehr einfach. Die Energieerhaltung ergibt sich, da die gegenseitigen Beschleunigungen sich aufheben müssen. Die Energie der Rakete hat sich real erhöht. Man schreibt dem Potential einfach eine negative Energie zu. Das Objekt, unsere Rakete, hat seine Raumzeitdichte beim Verlassen des Potentials aber tatsächlich erhöht. Das wird bei der Berechnung alles in einen Topf geworfen. Durch eine negative Energie im Potential bekommen wir die Energieerhaltung und die Berechnungen sind sehr einfach.
Wie verhält es sich hier beim Sonderfall Licht. Schauen wir uns ein Photon in der Wellenbeschreibung an, da ist es etwas einfacher. Das Photon muss nicht unbedingt langsamer werden, es kann noch etwas anderes machen. Wenn die Energie eines Photons durch seine Wellenlänge bestimmt wird und eine Beschleunigung einer Erhöhung der Energie entspricht, dann kann das Photon bei gleicher Geschwindigkeit seine Energie durch eine kleinere Wellenlänge erhöhen. Das ist die Blauverschiebung. Will das Photon aus dem Gravitationspotential wieder heraus, geht es umgekehrt und wir erhalten die Rotverschiebung. Es muss einen Teil seiner vorhandenen Raumzeitdichte gegen die Beschleunigung der Gravitation antreten lassen. Das funktioniert aber nur in das Potential hinein oder heraus.
Damit ist geklärt, woher das Äquivalenzprinzip kommt. Nochmals in kurzen Sätzen zusammengefasst:
Mit dieser kleinen Erklärung sollte nun auch klar sein, warum Lagrange und Hamilton so schön funktionieren. Dies kommt alles von der Energieerhaltung. Eine Raumzeitdichte kann sich selbst eben nur wandeln. Eine Raumzeitdichte kann sich selbst nicht vermindern oder vermehren, dies ist die Energieerhaltung. Mit diesem Wissen können wir uns der Kosmologie zuwenden. Die Entwicklung unseres Universums.