
Alles besteht aus Raumzeit
Wir starten mit der Superposition. Die machen wir als erstes, da in vielen Vorlesungen die Superposition als die grundlegendste Eigenschaft der QM bezeichnet wird. Der Lösungssatzsatz zur Superposition wird bei der Verschränkung und den Wahrscheinlichkeiten fast exakt gleich verwenden. Selbst der große Streitpunkt: lokal und nicht lokal, kann damit einfach erklärt werden. Daher werden wir die Idee zur Abbildung der Superposition etwas genauer beschreiben.
Bevor wir die Superposition über die DP erklären, sollte wir aber erst einmal besprechen, was unter einer Superposition verstanden wird.
Für eine Erklärung der Superposition ist die Mathematik hilfreich. Hier ist die Mathematik leichter zu verstehen als die logische Erklärung. Wir haben eine lineare Differenzialgleichung f(x), egal was es sein soll. Diese Abbildung besitzt eine Lösung L. Nun kann es sein, dass auch R eine Lösung von f(x) ist. Es können mehrere Lösungen vorhanden sein. Dann ist laut eines mathematischen Theorems auch L+R eine Lösung der Abbildung. Das funktioniert bei den linearen Differenzialgleichungen für die QM immer. Wichtig! Die zusätzliche Lösung ist nicht L oder R, sondern L+R. Die Kombination der Lösungen ist gleichzeitig auch eine neue Lösung. Dass funktioniert nicht nur mit zwei verschiedenen Lösungen. In der QM brauchen wir oft unendlich viele Lösungen. Das klingt mathematisch sehr einfach und ist es auch.
Die gesamte QM wird durch lineare Differenzialgleichungen abgebildet. Das ist auch gut so. Die QM ist sehr kompliziert. Nur weil diese eine lineare Abbildung ist, können wir überhaupt etwas berechnen. Dies bedeutet aber auch, ist die QM die korrekte mathematische Abbildung und davon gehen wir aus, da diese zu gut bestätigt ist, dann muss dieses Verhalten auch physikalisch so eintreten. Bei einer etwas abstrakten Beschreibung, wie zum Beispiel einem Spin eines Teilchens, haben wir mit so einer Aussage kein Problem. Dann hat ein Elektron eben eine Kombination von Spin up und Spin down gleichzeitig. Das bringt uns nicht um den Schlaf. Anders wird dies bei uns bekannten Zuständen. Hier setz auch Schrödinger mit seiner Katze an. Laut der QM ist eine Katze bei Schrödinger bis zur Messung gleichzeitig tot und lebendig. Das klingt für uns schon nicht mehr so verständlich.
Aus meiner Sicht ist aber der Ort eines Teilchens die beste Erklärung für die Superposition. Für uns kann ein Teilchen an genau einer Stelle in der Raumzeit vorhanden sein. Laut der QM ist dies so nicht richtig. Der eindeutig bestimmte Ort tritt nur bei einer Messung auf. Davor kann ein Teilchen an vielen Orten gleichzeitig sein. Jeder Ort ist möglich. Eventuell mit einer sehr kleinen Wahrscheinlichkeit, aber die Möglichkeit ist vorhanden. Dies bedeuten senden wir ein Teilchen aus, z.B. ein Elektron direkt gerade von uns weg. Dann ist es nur mit einer hohen Wahrscheinlichkeit auf einer geraden Strecke von uns weg unterwegs. Es kann aber auch links oder rechts von der Geraden sein. Dann eben mit einer geringeren Wahrscheinlichkeit. Dies bedeutet nicht, dass das Teilchen einen eindeutigen Ort besitzt und wir diesen bis zur Messung nur nicht kennen. Das Teilchen ist gleichzeitig an allen möglichen Orten vorhanden. Das kennen wir aus unserem Alltag nicht. Ok, wir sind manchmal der Meinung z.B. einen Schlüssel an genau dieser Stelle abgelegt zu haben und er ist nicht da. Das hat aber nichts mit Quantenmechanik zu tun. In unserer Alltagswelt und auch in der ART ist ein Objekt an genau einer Position vorhanden. Bei der QM hat das Teilchen die Position Links L, Mitte M, Rechts R und zusätzlich zusammen (L + M + R). Gerade beim Ort haben wir den schlechtesten Fall. Wenn wir nicht einen speziellen Aufbau für ein Experiment wählen, dann hat ein Teilchen als möglichen Aufenthaltsort die gesamte Raumzeit zur Verfügung. Das Elektron ist gleichzeitig im gesamten Universum vorhanden. Aus diesem mathematischen Ansatz heraus ist die Superposition rein logisch nur schwer zu verstehen.
Mit der SRT ist man sich evtl. beim Zeitpunkt, Abstand und der Energie nicht einig, da dies von Bewegungszustand abhängig ist. Aber in der SRT und der ART ist ein Objekt eindeutig an einem Ort. Ohne diese Eigenschaft können wir in der ART keine Aussage zu einem Objekt treffen. Wo soll die Gravitation/Raumzeitkrümmung sich hin ausrichten, wenn die Energie/Raumzeitdichte keinen eindeutigen Ort besitzt? Das ist das Grundproblem bei der Vereinigung von ART und QFT. In der QM ist die Superposition aller Eigenschaften eines Objektes der grundlegende Aufbau der Beschreibung. Damit ist ein Objekt oder eine Wechselwirkung nicht lokal. Dies bedeutet, dass die Eigenschaften und Wechselwirkungen keine eindeutige Position haben. In der ART sind alle Objekte lokal. Diese müssen eine eindeutige Position besitzen. Die Gravitation könnte sich sonst nicht ausrichten oder der Impuls hat keine klare Richtung.
Das nächste Problem ist, dass die QFT oder die QM die Superposition nicht erklärt. Die mathematischen Beschreibungen wurden so gewählt, dass diese dem experimentellen Befund entsprechen. Dies ist das übliche Vorgehen. Auch bei der Gravitation ist dies so passiert. Einstein hatte die Idee mit der geometrischen Abbildung in der Raumzeit. Die Feldgleichungen wurden so aufgebaut, dass diese der damals bekannten Physik entsprechen. Es wurde z.B. für die Energieerhaltung eine größere Veränderung vorgenommen. Aus der mathematischen Beschreibung sind dann Vorhersagen wie Schwarze Löcher, Gravitationswellen usw. entstanden, die alle ohne Einschränkungen bestätigt wurden. In der QM war es nicht anders. Um den Doppelspalt und das Wasserstoffatom erklären zu können, musste die QM als eine lineare Beschreibung mit Superposition und Wahrscheinlichkeit aufgebaut werden. Alle weiteren Aussagen der QM, wie z. B. die Unschärferelation sind rein über die mathematische Beschreibung gefunden worden und haben sich im Anschluss alle als richtig herausgestellt. Egal wir verrückt die Aussagen für unsere Alltagswelt auch klingen mögen.
Bei ART und bei QM kann nicht angegeben werden, warum wir diese Abbildung wählen müssen. Bei der ART ist der Gedanke von Einstein mit einer geometrischen Abbildung in der Raumzeit noch halbwegs „alltagstauglich“. Daher gibt hier weniger philosophische Streitpunkte zu besprechen. Das Hauptthema ist fast immer, wie die Raumzeit selbst zu verstehen ist. Im Jahre 2026 ist gerade die Diskussion, ist die Raumzeit fundamental oder emergent, ein aktuelles Thema.
Bei der QM ist das viel schwieriger, da die Anzahl der Themen viel größer ist. Das kommt daher, da die QM eine fast rein mathematische Entwicklung durchlaufen hat. Ein verständliches allgemeines Grundkonzepte, wie eine geometrische Abbildung in der Raumzeit, gibt es hier nicht. Damit ist aus philosophischer Sicht alles in der QM „fragwürdig“. Es ist keine eindeutige logische Grundlage vorhanden. Dies führt dazu, dass es eine fast unüberschaubare Menge an „Auslegungen“ zur QM existieren. Als Beispiel nehmen wir hier die Kopenhagener Deutung der QM. Das ist bereits eine Sammlung von verschiedenen Auslegungen. Hier geht man so weit, dass ein Teilchen zwischen zwei Punkten keine Strecke/Pfad zugewiesen werden kann. Selbst die Existenz des Teilchens wird bis zu einer Messung nicht anerkannt.
Wir wollen dieses Dilemma auflösen. Wir werden zu allem in der QM eine Begründung abgeben. Gleich vorab: Die Kopenhagener Deutung müssen wir ablehnen. Tatsächlich ist die Beschreibung der QFT mit Pfadintegralen eine geeignete mathematische Abbildung auf Grundlage der DP. Die verschiedenen Pfade existieren und werden auch durchlaufen. Nur nicht in unserer Raumzeit.
Dann suchen wir mal nach einer möglichen Abbildung der Superposition in der DP. Wie immer haben wir nicht viele Möglichkeiten. Es wird bei fast allen Themen in der QM, auf einer Abbildung in einer niederdimensionalen Raumzeit hinauslaufen. Der Knackpunkt ist die Schnittstelle zwischen 3D und 2D. Wir erhalten für eine Raumzeitdichte immer zwei grundsätzlich verschiedene Darstellungen. Eine in 3D, nach ART und gleichzeitig unendlich viele Darstellungen in 2D, nach QM. Das bedeutet wir lösen die zwei unvereinbaren Darstellungen von ART und QM nicht in einer einzigen Darstellung auf. Diese „einzige“ Darstellung ist der eigentliche Wunsch bei einer Vereinigung von ART und QFT. Wir müssen diese zwei Darstellungen beibehalten und verbinden diese über die niederdimensionale Grenze. So wird es funktionieren.
Zum Start haben wir erstmal das identische Problem wie ART zu QM. Eine Raumzeitdichte in unserer Raumzeit hat eine eindeutige Position. Das muss so sein, sonst funktioniert die ART nicht mehr. Dies bedeutet, das Elektron vor unserer Nase, welches wir in einer geraden Linie von uns weg beschleunigen wollen, macht auch genau das, was wir klassisch nach Newton von einem Teilchen erwarten würden. Es ist nicht links oder rechts, sondern in der Mitte mit einem geraden Impuls Richtung Ziel. Das hat im ersten Ansatz nichts mit einer QM zu tun. Das ist auch nur eine Seite der Medaille. Der Teil aus der Sicht unserer 3D Raumzeit.
Auf die QM kommen wir, denn jedes 3D Raumzeitvolumen und eine Raumzeitdichte ist nichts anderes, hat immer unendlich viele 2D Raumzeiten zur Abbildung zur Verfügung. Eine Raumzeitdichte hat damit immer zwei gleichzeitig gültige Beschreibungen:
Mit den unendlich vielen niederdimensionalen Raumzeiten können wir von jedem beliebigen Punkt unserer Raumzeit mindestens eine Gerade in die Raumzeitdichte des Elektrons legen. Einfach aus diesem Gedanken heraus ist es möglich, jeden beliebigen Raumzeitpunkt in 3D über 2D zu erreichen. Eine Raumzeitdichte aus 3D kann damit einen Raumzeitpunkt auch abseits von seiner 3D Wegstrecke erreichen. Diese aber ausschließlich über 2D.
Wichtig: Wir haben über 2D unendlich viele Pfade, von einer Raumzeitdichte mit ihrem lokalen Volumen in 3D, zu jedem möglichen Raumzeitpunkt der 3D Raumzeit. Diese Pfade sind alle gleichzeitig in 3D vorhanden. Damit müssen sich diese in 3D gegenseitig beeinflussen. Wie dies genau passiert, kommt in den späteren Kapiteln zur Mathematik und stellt dann die Interferenz der Möglichkeiten dar. Die 3D Raumzeitdichte hat schon noch ein Wort mitzureden.
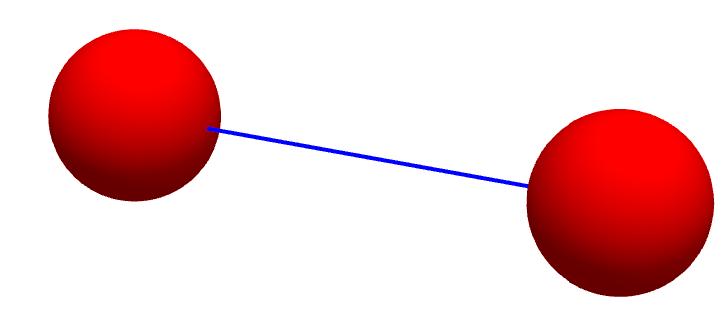
Die gerade Linie als Verbindung passt noch nicht. Unsere Raumzeit ist 3D, damit muss die Verbindung eine Fläche 2D sein. Wir kommen immer nur eine Raumdimension tiefer.
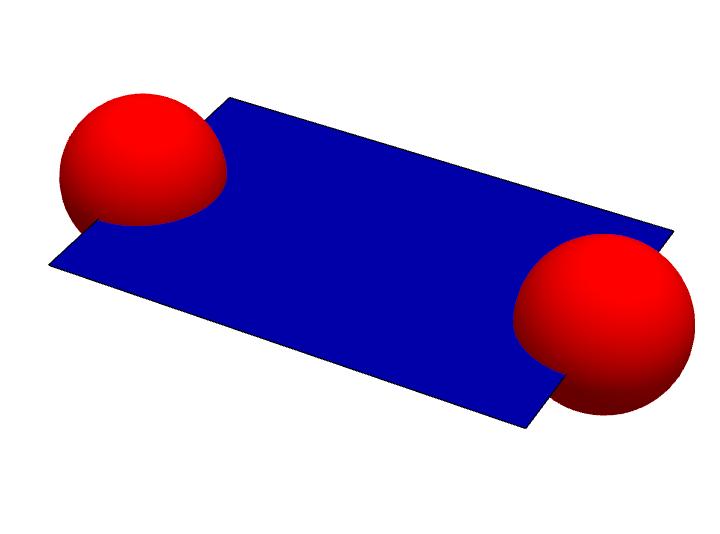
Das ist genau eine Möglichkeit der Verbindung. Wenn wir die Fläche zwischen den zwei Volumen um die Verbindungsline rotieren lassen, können wir unendlich viele 2D Raumzeiten zwischen dieser Strecke legen. Allein damit können wir bereits alle Raumzeitpunkte in unserer Raumzeit erreichen. Das ist aber noch zu wenig. Wer sagt denn, dass die 2D Raumzeit zwischen den Volumen gerade sein muss. Es gibt viel mehr Möglichkeiten die Punkte über eine extrinsisch gekrümmte 2D Raumzeit zu erreichen.
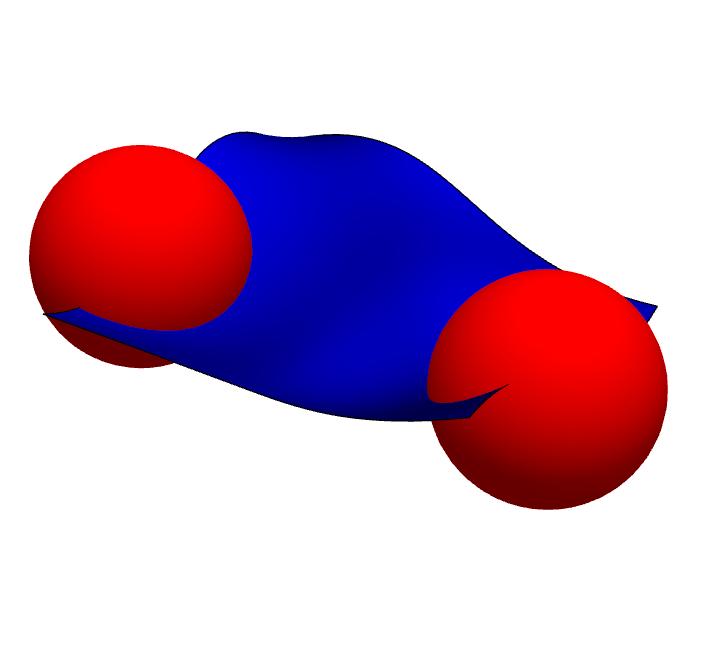
Allerdings gibt es dann doch eine wichtige Einschränkung. Für eine Verbindung haben wir nur eine „Sorte“ an Objekten zur Verfügung, Raumzeiten. Alle Felder der QFT und damit auch die möglichen Pfade, werden bei uns durch Raumzeiten aufgebaut. In der DP steht uns kein anderes Objekt zur Verfügung. Damit eine Raumzeit über die ART beschrieben werden kann, benötigt die Raumzeit bestimmte Eigenschaften. Die zwei grundlegenden Eigenschaften sind: Kontinuität und Differenzierbarkeit. Für die ART brauchen wir dann noch eine bestimmte „Sorte“ an Differenzierbarkeit, dies ist hier aber nicht relevant. Diese beiden Bedingungen werden in jeder beliebigen n-dimensionalen Raumzeit zwingend benötigt.
Wir benötigen die Kontinuität, weil wir sonst andere Raumzeitgrenzen erhalten würden. Eine Raumzeit darf keine „Lücke“ haben. Weder in 3D noch in 2D, sonst gibt es evtl. auch keine Verbindung.
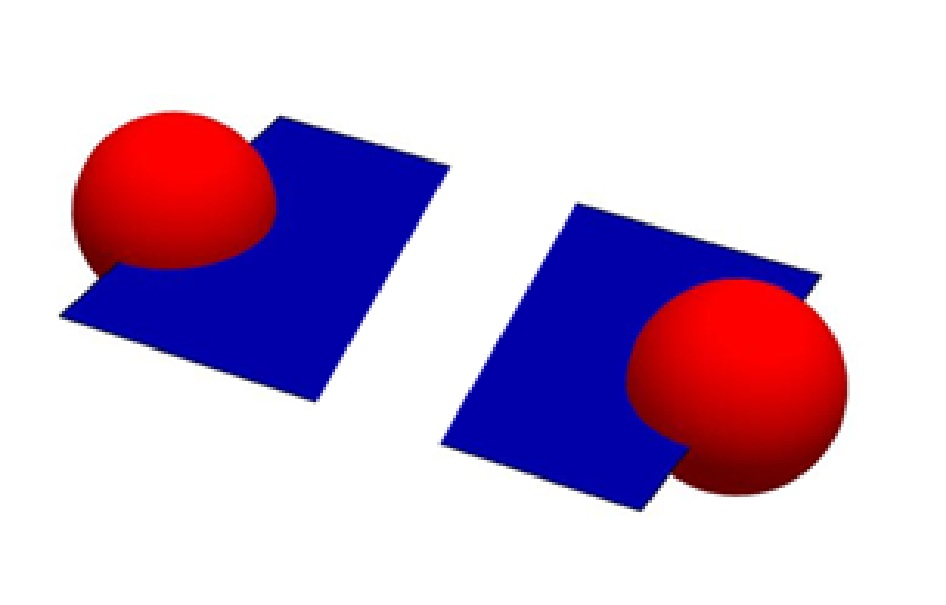
So darf es nicht aussehen.
In jeder Raumzeit hat die Abbildung einer Raumzeitdichte immer eine Verbindung zu jedem anderen Punkt in der Raumzeit. Nochmal zur Wiederholung:
Damit hat das Elektron bereits in 3D eine Verbindung zu jedem möglichen Raumzeitvolumen. Es gibt innerhalb einer Raumzeit keine Grenzen. Nur die Überbrückung der vom Impuls abweichenden Strecke geht nicht direkt in 3D. Für den geraden Weg brauchen wir keine Beschreibung über die QM.
Durch die 2D Raumzeiten hat das Elektron zusätzlich unendlich viele Pfade zu jedem beliebigen Raumzeitpunkt erhalten. Es dürfen aber nur diese Pfade gezählt werden, die durchgängig und damit kontinuierlich sind. Tatsächlich werden wir später beim Doppelspaltexperiment sehen, dass wir dieses Experiment nicht erklären können, wenn wir annehmen, dass ein Elektron von der Quelle zum Ziel (Detektorschirm) direkt ohne einen Pfad „springen“ kann. Dann würde es keine Rolle spielen, ob es ein Doppelspalt ist oder nicht. Ein echtes „beamen“, wie in Star Trek von Quelle zu Ziel geht hier auch nicht. Es müssen Pfade vorhanden sein. Die Regel ist aber, habe ich mindestens einen Pfad in 3D, so sind immer unendlich viele in 2D vorhanden.
Die Differenzierbarkeit ist ein einfacher mathematischer Begriff. Am besten lässt sich dieser mit einer „runden und zusammenhängende Geometrie ohne Ecken und Kanten“ übersetzen. Hier sagt ein Bild tatsächlich mehr als 1000 Worte.
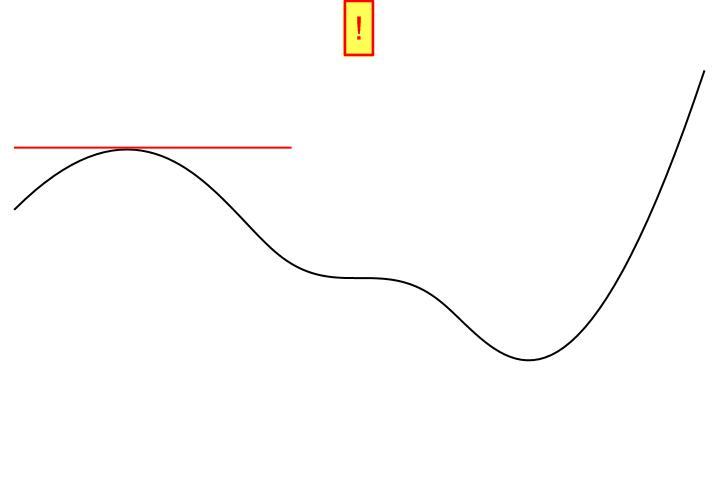
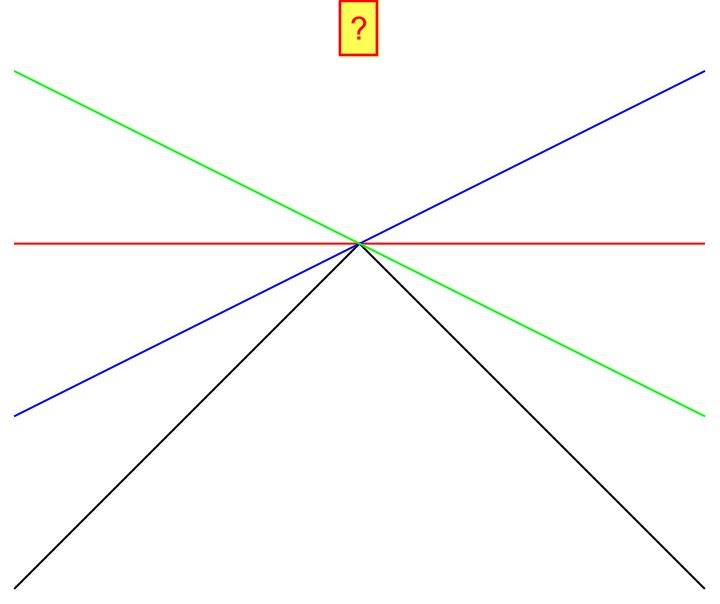
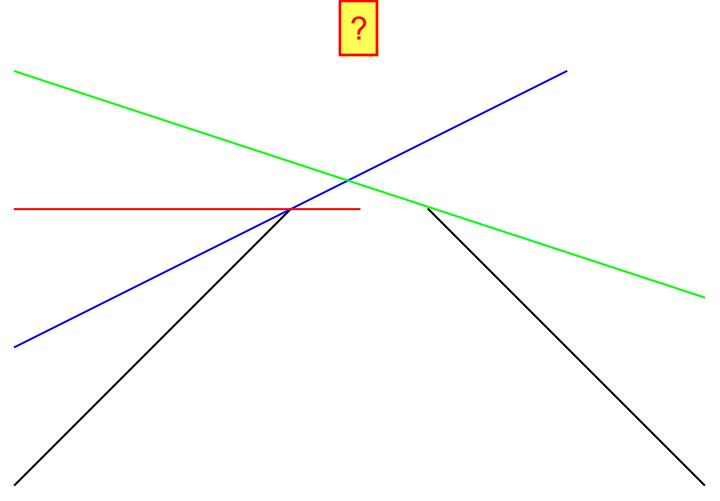
Wenn man von links und von rechts auf einen bestimmten Punkt einer Funktion zuläuft, dann muss man dort eine eindeutige Tangente anlegen können. Bei einer „runden“ Abbildung einer Funktion ist dies immer möglich. Bei der Funktion mit der Ecke oder Kante, geht dies nicht. Dort könnte man unendlich viele Tangenten anlegen. Genau dieser Punkt ist nicht differenzierbar. Unser Argument der Kontinuität spielt hier auch mit. Wenn es einen Sprung gibt, so könne wir an dem Sprung keine eindeutige Tangente anlegen. Soweit die einfache Mathematik.
Warum ist diese Differenzierbarkeit für uns so wichtig? Zur Erinnerung: Raumzeitdichte ist Energie, Geometrie und Bewegungszustand. Die Raumzeitdichte wird direkt in der Geometrie der Raumzeit abgebildet. Damit auch der Bewegungszustand. Die geometrische Abbildung eines Bewegungszustandes ist die Differenzierbarkeit.
Keine Differenzierbarkeit => kein Bewegungszustand => keine Raumzeitdichte => keine Raumzeit. Raumzeitdichte ist Raumzeit selbst. Mit einer nicht differenzierbaren Raumzeit könnten wir bei unserem Ansatz nichts anfangen.
Für die mathematische Abbildung wird diese Eigenschaft dann nochmal wichtig. Das hat Einfluss auf den Aufbau der Schrödingergleichung. In 3D gibt es in der Raumzeit Veränderungen, damit müssen wir zweifach Ableiten können. In 2D ist alles statisch. Dort reicht eine einfache Ableitung. Da wir nur „runde“ Abbildungen zulassen können, wird sich explizit eine Wellenbeschreibung anbieten. Die flache Raumzeit ist der Sonderfall. Dazu aber mehr im Kapitel zur Mathematik.
Eine entscheidende Frage ist: Wie überbrücken wir den die Distanz in 2D? Die Antwort ist etwas anders, als wir es im ersten Schritt vermuten würden. In 3D, also der Raumzeit mit der Raumzeitdichte, ist der Impuls (gerichtete Raumzeitdichte) die Antwort. Selbst wenn für eine Strecke, in einer 2D oder 1D Raumzeit, eine bestimmte Zeit für die Überbrückung der Strecke benötigt wird, es geht keine Zeit über die Schnittstelle. Daher kann der Vorgang so lange dauern, wie er will. In unserer 3D Raumzeit wird jeder niederdimensionale Vorgang immer instantan passieren. Wir kennen nur die Zeit in unserer Raumzeit. Wir müssen für die QM aber speziell eine 2D Raumzeit benutzen. Dort sind alle Abbildung statisch. Das hatten wir schon bei der Kosmologie. Wie soll eine Abbildung, z.B. als Schwarzes Loch, in 2D die Strecke Überbrücken, wenn es keine Veränderung in der Raumzeit geben darf?
Wer hier mal 2 – 3 Minuten investieren will und selbst auf die Lösung kommt, hat die Grundidee zur DP verstanden.
Das Schwarze Loch oder die extrinsische Raumzeitkrümmung in 2D muss die Strecke gar nicht überbrücken. Nochmal, jede n-dimensionale Raumzeitdichte ist die n-dimensionale Raumzeit selbst. Wenn die 2D Raumzeit Ziel und Quelle in 3D verbindet, dann ist bereits alles zur Überbrückung mit einer Raumzeitdichte vorhanden. Eine Raumzeit und damit eine Raumzeitdichte in 2D verbindet in 3D die Orte, einfach nur durch ihre Existenz. Das die 2D Raumzeit selbst eine extrinsische Verformung besitzt oder eine intrinsische Verformung als Schwarzes Loch hat, spielt für die Verbindung keine Rolle. Die Verbindung/Raumzeit bildet mit diesen Verformungen nur die Eigenschaften der Teilchen ab. Die Existenz der Teilchen ist aber die Raumzeit selbst. Wo diese Eigenschaften auf der „Stecke“ liegen ist egal. Wir können aus dem niederdimensionalen keine geometrische Größe wie Strecke/Länge usw. erkennen.
Wichtig sind nur zwei Eigenschaften.
Das bedeutet, dass gerade in den ersten Bildern eingezeichnete flache 2D Raumzeit ohne eine Schwarzes Loch von 3D nicht erkannt werden kann. Dazu später beim Standardmodell mehr.
Aus dieser Überbrückung einer Strecke in 2D können wir aber eine Forderung an die QM stellen. Alle erkennbaren Wechselwirkungen aus 2D in 3D müssen immer und ohne Ausnahme instantan erfolgen. Wenn eine Wechselwirkung eine Verzögerung hat, so stammt dieser Teil immer aus unserer Raumzeit. Wir werden dies bei der Verschränkung nochmals aufgreifen.
Wenn wir von einer einzigen Raumzeitdichte in 3D unendlich viele Abbildung als Raumzeitdichte in 2D erhalten, haben wir dann nicht die wundersame Energievermehrung? Nein, zum Glück nicht. In der DP bleibt die Energieerhaltung weiterhin gültig. Allerdings nur separat je Raumzeit.
Tatsächlich ist dieses Thema nicht so leicht zu beantworten, es hat viele unterschiedliche Facetten. Das ist die Beschreibung der Schnittstelle zwischen 3D und 2D. Genau dies ist der gesamte Teil 3. Daher teilen wir das in zwei Bereiche auf. Für den ersten Bereich, die Angabe der Energie, gibt es in diesen Abschnitt die Antwort. Für alle andern offenen Fragen dazu und dies sind einige, werden wir dies in den jeweiligen Abschnitten in Teil 3 erklären.
Die Energie kann über die dimensionale Grenze hinweg nicht übertrage werden, da keine Zeit übertragen werden kann. Energie ist nur in Zusammenhang mit einer Angabe von Zeit erklärbar. Daher kommt:
Raumzeitdichte = Energie = Raumzeitgeometrie = Bewegungszustand. Eine Angabe ohne Zeit ist keine vollständige Abbildung in der Raumzeitgeometrie oder des Bewegungszustandes. Ohne Zeit keine Energie. Damit wird von 3D auf 2D, aus der Sicht von 3D, keine Energie übertragen. In 3D bleibt die Raumzeitdichte genau das, was diese ist. Die Raumzeitdichte in 3D gibt keine Energie in eine 2D Raumzeit ab.
Wie sieht es in 2D aus? Da wird doch eine Raumzeitdichte abgebildet und damit auch Energie. Ja, das ist so. Aber die Energie existiert nur begrenzt in dieser Raumzeit, als zusätzliche Abbildung zur 3D Raumzeitdichte. Die Abbildung in 3D und in 2D gehen auf die identische Energie zurück, ohne das 3D an 2D Energie abgeben muss. Damit kann dieses Prinzip unendlich oft angewendet werden. Allein schon die Existenz einer 2D Raumzeit ist eine Raumzeitdichte und damit eine Energie. Nur zählt diese gar nicht in 3D als Energie. Dazu muss die 2D Abbildung die Grenze zu 3D überbrücken und geht damit über die Quantisierung als Wirkung in 3D ein und nicht direkt als Energie. Das beschreiben wir genauer in der Quantisierung. Wie die einzelnen Abbildungen in 2D aussehen, schauen wir uns dann beim Standardmodell genauer an.
Damit könnten wir bei der Superposition doch schon fertig sein? Die Superposition ergibt sich, da wir unendlich viele 2D Abbildungen gleichzeitig haben. Wobei das Wort „gleichzeitig“ hier mit Vorsicht zu genießen ist. In der QM gibt es genauso wie in der Relativitätstheorie keine Gleichzeitigkeit mehr. In der Relativitätstheorie wegen der maximalen Lichtgeschwindigkeit. Bei der QM gibt es zwischen den verschiedenen Raumzeiten noch nicht einmal einen zeitlichen Bezug. Das wird dann später wichtig, wenn wir das Doppelspaltexperiment besprechen. Gleich vorab, da wird niemals etwas rückwärts in der Zeit verändert. Es gibt kein vorwärts oder rückwärts zwischen den Raumzeiten.
Es gibt aber noch einen zweiten Aspekt zur Superposition der hier wichtig ist. Die Superposition gibt es auch bei Eigenschaften, die nicht den Ort betreffen. Wenn wir überall und in allen Eigenschaften eine Superposition haben wollen, dann muss auch die einzelne 2D Abbildung eine spezielle Geometrie haben. Um dem Beispiel mit dem Ort treu zu bleiben, beschreiben wir dies an einen Effekt, denn es nur in der QM gibt, den Tunneleffekt.
Die Besonderheit in der geometrischen Abbildung in einer einzelnen 2D Raumzeit wird sehr schön durch den Tunneleffekt beschrieben. Wir nehmen wieder unser Elektron, dass wir in gerader Linie von uns wegschießen. Diesem Elektron stellen wir ein Hindernis in den Weg. Dabei braucht das Hindernis keine Struktur aus Ruhemasse zu sein, wie z.B. eine dünne Wand. Es reicht auch ein starkes elektrisches Feld, durch das ein geladenes Teilchen nicht kommen darf.
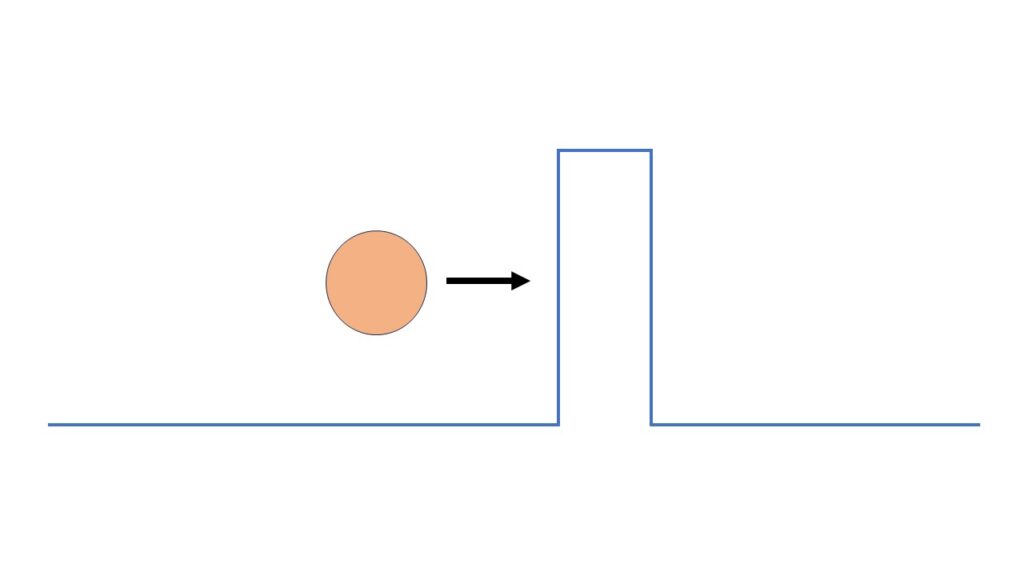
Unsere Erwartung ist, dass das Elektron es nicht durch die Wand schafft. So auch die Beschreibung der klassischen Physik. In der QM darf das Elektron, wenn auch nur mit geringer Wahrscheinlichkeit, durch das Hindernis hindurch auf die andere Seite kommen. Der Grund sollte uns nun klar sein.
Wir bilden einfach alles als Geometrie in kontinuierlichen und differenzierbaren Raumzeiten ab. Daraus folgt, dass eine „digitale“ Abbildung, obwohl wir von einer Quantenmechanik sprechen, nicht möglich ist. Die Raumzeitdichte des Elektrons wie auch des Hindernisses dürfen nicht wie folgt aussehen.
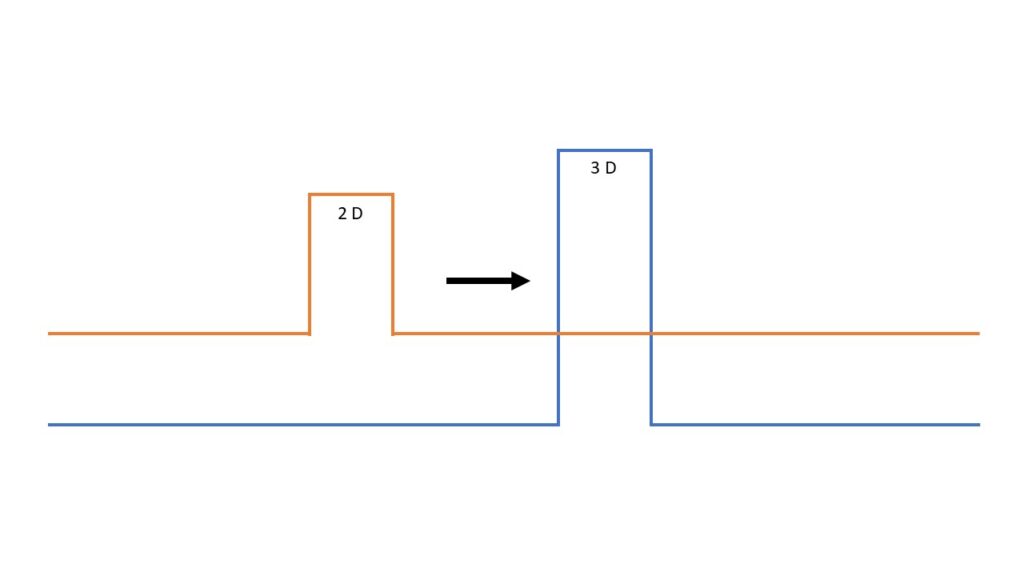
Beide Objekte sehen in 3D wie auch in 2D immer so aus.
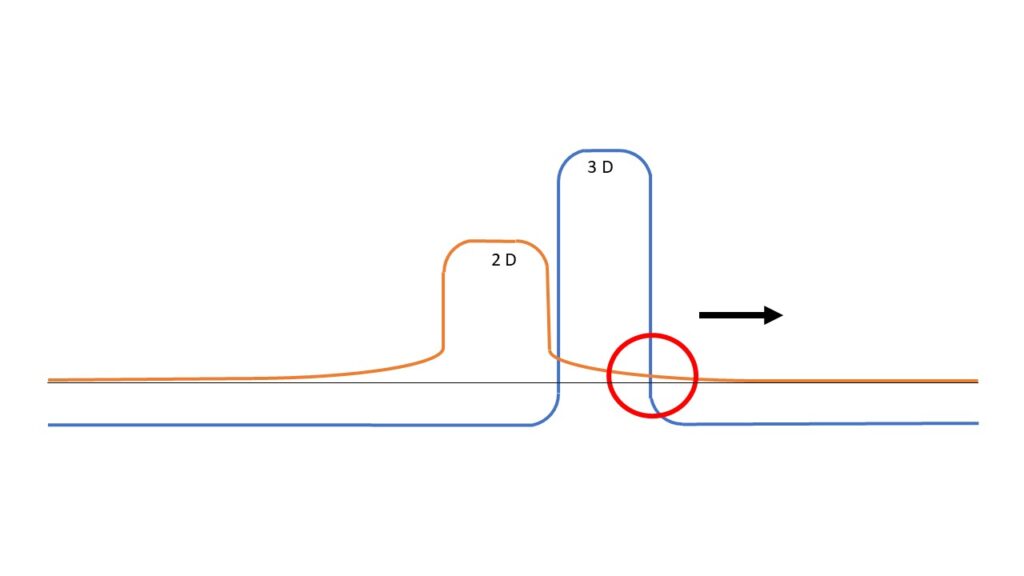
Damit hat diese Wellenabbildung immer die zwei, für das Tunneln, wichtigsten Eigenschaften.
Wenn man so will, ist die Bezeichnung Quantenmechanik aus dem Blickwinkel der geometrischen Abbildungen vollkommen falsch gewählt. Die Abbildung darf nicht quantisiert sein. Wir erzeugen immer eine mögliche Überschneidung der geometrischen Abbildungen. Das ist der rote Kreis und dieser liegt hinter dem Hindernis. Wie wir das Elektron dort messen, machen wir später. Wechselwirkung und Messung besprechen wir in einem separaten Kapitel.
Die Überbrückung der Strecke kann aber nur in 2D erfolgen. In 3D blockt das Hindernis die Raumzeitdichte ab. So ist der Versuchsaufbau. Damit können wir fordern, dass der Tunneleffekt immer instantan passieren muss. Zusätzlich müssen der Tunneleffekt und die Superposition für alle Eigenschaften eines Teilchens vorhanden sein. Wir bilden alles über die Geometrie der Raumzeit ab. Damit treten die Superposition und der Tunneleffekt nicht nur bei Impuls oder Ort auf. Hier können wir es aber sehr anschaulich darstellbar. Wie wir später im Kapitel zur Mathematik der QM sehen werden, ist die kontinuierliche und differenzierbare Raumzeit der Grund für die Wellenbeschreibungen.
Die Superposition kommt daher, dass wir unendlich vielen niederdimensionalen Abbildungen haben, welche sich gegenseitig in 3D bedingen. Jede einzelne Abbildung steht für sich in 2D. In 3D liegen aber alle Abbildungen zusammen. Daher ergibt sich nicht die Lösung L, M und R einzeln, sondern auch L+M+R zusammen in 3D. Unsere Messung passiert immer in 3D. Daher darf bis zur Messung das Verhalten einer Superposition vorhanden sein. Danach nicht mehr.
Das große Problem der Lokalität gibt es in der DP gar nicht. In jeder n-dimensionalen Raumzeit ist die Raumzeitdichte immer lokal. In 2D sind unendlich viele Abbildung gleichzeitig in 3D vorhanden. Damit darf in der QM kein lokales Verhalten vorhanden sein. Lokal und nicht lokal sind nur die verschiedenen „dimensionalen Ausprägungen“ einer einzelnen Raumzeitdichte. Zum Problem wird dies nur, wenn wir beide Seiten der Medaille in einer einzigen Raumzeit abbilden wollen. Das ist aber laut DP nicht möglich. In der DP ist die Fragestellung zur Lokalität in einer Raumzeit bereits als Frage falsch.
Tatsächlich gibt es ein Objekt, dass bereits in 3D ohne 2D ein eindeutiges lokales verhalten aufweist, das Schwarze Loch. Da die Raumzeitdichte im Zentrum des Schwarzen Loches keine niederdimensionale Abbildung haben kann, gibt es hier keine Superposition und damit kein nicht lokales Verhalten. Dies kann man auch an der Hawking-Strahlung erkennen. Würde das Schwarze Loch und damit der Ereignishorizont keine eindeutige Position in unserer Raumzeit haben, so könnte sich keine Hawking-Strahlung bilden. Da sich die einfallenden wie auch entkommenden Teilchen, bei einer schwankenden Grenze, statistisch ausgleichen würden. Hawking-Strahlung funktioniert nur, wenn der ART-Teil der Gleichung lokal bleibt und die Quantenfluktuationen es nicht sind. Dieses Verhalten lässt sich nur erklären, wenn das Schwarze Loch mit seinem Ereignishorizont keine quantenmechanische Abbildung hat.