
Alles besteht aus Raumzeit
In diesem Kapitel werden wir die wichtigste Schlussfolgerung aus der Annahme der Raumzeitdichte herleiten. Unsere und jede andere Raumzeit besitzt Grenzen. Aus den Grenzen leiten wir ab, dass es unendlich viele Raumzeiten in verschiedenen Konfigurationen gibt. Auch die Definition der Raumzeitdichte erfährt hier eine exakte Beschreibung. Das Thema kann gar nicht hoch genug bewertet werden. Die gesamte Kosmologie und QM hängt von diesem Thema ab. Ohne das Verständnis zu den Grenzen der Raumzeit brauchen wir die weiteren Kapitel gar nicht anfangen. Daher dieses Kapitel lesen, wenn Zeit und Ruhe vorhanden sind. Die weiteren Zutaten nach Zeit und Ruhe, sollen hier jedem selbst überlassen sein. Mein Vorschlag sind Gummibärchen und ein Gläschen Wein. Das Kapitle evtl. doppelt lesen, bis die Grundlagen sitzen.
Bevor wir alle Punkte in Detail durchgehen, kommt hier eine Übersicht, was wir alles besprechen müssen. An der Anzahl und Wichtigkeit der Punkte könnt Ihr bereits die hohe Priorität der Raumzeitgrenzen erkennen:
Mache Punkte werden evtl. nicht zu 100% komplett ausgearbeitet. Dann werden diese bei den jeweiligen speziellen Themen wieder aufgegriffen. Hier geht es hauptsächlich um die Struktur der Raumzeiten. Insbesondere das Zusammenspiel von unterschiedlichen Raumzeitkonfigurationen wird in der Kosmologie und in der QM beschreiben.
Wie kommen wir auf die Idee, dass die Raumzeit eine Grenze besitzt? Zurzeit, das ist das Jahr 2026, gilt diese Frage in der Lehrbuchphysik als nicht entschieden. Aus unserer Alltagserfahrung heraus hat, absolut jedes Objekt, eine begrenzte Ausdehnung. Irgendwann hört ein Objekt auf und es gibt dann einen weiteren umschließenden Raum für das Objekt.
Bei der Raumzeit ist die nicht der Fall. Der Grund ist einfach. Die Raumzeit definiert was eine Länge oder eine Zeit ist. Das war unser Ansatz für die Raumzeitdichte. Damit gibt es außerhalb einer Raumzeit keine gültige Definition eines Abstandes oder einer Zeit. Diese Definition existiert immer nur innerhalb einer Raumzeit. Die Definition kann in verschiedenen Raumzeitkonfigurationen unterschiedlich ausfallen, aber ohne eine Raumzeit keine Definition von Raum und Zeit. Wie wollen wir dann die Grenze der Raumzeit festlegen, wenn es keinen weitere umgebende Raumzeit gibt und damit kein „Außerhalb“ der Raumzeit.
Eine mögliche Lösung: Da sind evtl. noch andere Raumzeiten, in der unsere Raumzeit eingebettet ist. Wir werden in diesem Kapitel lernen, dass dies tatsächlich so ist. Diese Umgebung wird uns aber, für die Angabe eines Abstandes oder der Zeit außerhalb unserer Raumzeit, überhaupt nichts nützt. Eine Raumzeit definiert die Länge und die Zeit nur für sich selbst. Von Newton zu Einstein wurde Raum und Zeit von getrennten Objekten mit absoluten Angaben zu einem einzigen Objekt mit dynamischen Verhalten von Raum und Zeit. Wir gehen noch einen Schritt weiter und werden die Definition von Raum und Zeit in jeder Raumzeit separat haben. Damit dürfen wir nun nicht mehr annehmen, dass unsere Raumzeit in irgendeiner anderen Raumzeit einen Abstand oder eine Zeit definiert. Nochmal, jede Raumzeit ist ein eigenes separates Objekt, welches nur für sich eine Länge und eine Zeit definiert. Dies wird eine der wichtigsten Aussagen zu diesem Kapitel. Das bedeutet, dass wir mit einer Angabe von Länge, Volumen oder Abstand, aus der Raumzeit heraus keine Grenze setzen können. Wir brauchen eine andere Idee.
Wenn wir die Raumzeit als solche untersuchen wollen, dann können wir uns am besten die Verformungen der Raumzeit ansehen. Wie bei den Annahmen schon angedeutet, können wir letztendlich nichts anderes erkennen. Wie gehen wir vor? Wir haben die Raumzeitdichte neu ins Spiel gebracht, dann schauen wir uns diese doch mal bei Ihren extremen Werten an. Für neue Objekte wie die Raumzeitdichte, ist es immer eine gute Idee, diese Objekte in Ihren Extremen zu untersuchen.
Wir wollen die Raumzeitdichte gegen null gehen lassen. Dafür müssen die Zeit- und Raumdimension ihre Definition von Länge und Zeit gegen unendlich gehen lassen. Zeitrelaxation und Längenrelaxation. Diese Namen hatten wir so festgelegt. Diese „Gegenverformung“ zur Raumzeitdichte wird im Kapitel zur Kosmologie nochmals wichtig. Das wird unsere Expansion der Raumzeit (nicht nur des Raumes) ergeben.
Wir erhalten keine Grenze. Die Raumzeitdichte nimmt ab, wird aber niemals null werden. Das klären wir noch genauer in einem späteren Abschnitt. Entscheidend für uns hier ist, dass die Raumzeit in diesem Fall keine Grenze besitzt. Wenn uns dieser Weg nichts bringt, dann versuchen wir eben das Gegenteil.
Die Zeit- und Raumdimension gehen bei höherer Energie mit ihren Definitionen identisch gegen null. Damit wird die Raumzeitdichte immer größer und geht gegen unendlich. Wenn beide Dimensionen linear gegen null gehen, muss der Anstieg der Raumzeitdichte, mindestens quadratisch ausfallen. Es muss aber die bereits größere Raumzeitdichte immer weiter verdichtet werden. Daher ist der Anstieg der Raumzeitdichte, bei linearer Zeitdilation und Längenkontraktion sogar exponentiell. Die Raumzeitdichte ist die Energie. Das ist durch unseren Ansatz (Quelle der Gravitation) explizit so festgelegt worden. Damit wird bei einer linearen Erhöhung der Energie der Anstieg der Raumzeitdichte immer weniger werden. Der Anteil an der Erhöhung der
Gesamtenergie, nimmt durch die gleiche Menge an Energie immer weiter ab. Daher muss für einen linearen Anstieg der Raumkontraktion und Zeitdilatation eine exponentiell wachsende Energiemenge aufgebracht werden.
Zusätzlich muss es für das „kleiner werden“ der Zeit- und Raumdimension eine nicht überschreitbare Grenze geben. Wenn wir bei den Definitionen der Dimensionen bei null angelangt sind, ist Schluss. Weiter kann es nicht gehen. Vor dieser Grenze muss die Raumzeitdichte gegen unendlich gehen. Zusätzlich kann eine Raumzeitdichte, die alle Raumdimensionen belegt, nicht auf einmal eine Raumdimension verlieren. Diese ist in der Raumzeit vorhanden. Es muss in der Belegung der Raumdimensionen („innerer Aufbau“/QM) bereits festgelegt sein, ob diese Grenze erreichbar ist oder nicht.
Damit können wir eine Grenze erhalten. Diese hat ein sehr eigenartiges Verhalten. Die Grenze ist nur erreichbar, wenn mindestens eine Raumdimension und die Zeitdimension bereits von Anfang an bei der Raumzeitdichte nicht belegt ist. Sind alle Raumdimensionen belegt, kann weder die Raumdimension noch die Zeitdimension diese Grenze erreichen. Das ist ein sehr strikter Schalter für das Erreichen dieser Raumzeitgrenze.
Was wir brauchen, ist nun klar. Eine absolute Grenze innerhalb der Raumzeit, welche von bestimmten Objekten nicht erreicht werden kann und für Objekte, welche auf dieser Grenze liegen, die Existenzbedingung ist. Wir brauchen eine Zeitdilatation gegen null und eine Längenkontraktion gegen null. Das kennen wir doch, genau die Lichtgeschwindigkeit. Daher ist die Lichtgeschwindigkeit, als Grenze der Raumzeit, eine Veränderung der Struktur innerhalb der Raumzeit. Jeder Raumzeitpunkt kann diese Grenze erfahren. Dieser muss nicht an einem Rand liegen. Einen Rand, wie bei einem normalen Objekt des Alltages, gibt es in der Raumzeit nicht. Nehmen wir eine Raumdimension weg, dann müssen wir uns wohl auf der niederdimensionalen Grenze der Raumzeit befinden. Natürlich ist dann auch die Zeitdimension auf null. Wenn wir die Raumzeit als ein einziges Objekt identifizieren wollen, dann dürfen wir beim Verlassen der Raumzeit keine Zeit mehr haben. Raum und Zeit sind ein einziges Objekt und damit nicht trennbar. Das Verlassen einer Raumzeit wird damit durch eine Strukturveränderung hervorgerufen. Warum wir ein Objekt (Raumzeitdichte) mit Lichtgeschwindigkeit überhaupt noch in unserer Raumzeit wahrnehmen können ist ein weiteres Thema für dieses Kapitel. Hier wollen wir festhalten:
Eine Raumzeit besitzt eine Grenze
Die Lichtgeschwindigkeit c ist, laut dem Lehrbuch, durch ein Postulat der SRT, die festgesetzte maximale und für alle Beobachter identische Geschwindigkeit in unserer Raumzeit. Damit ist diese schon immer eine Grenze. Was soll an der Sichtweise der DP so besonders sein? Diese Grenze ist eine besondere Grenze. Schauen wir uns die Lichtgeschwindigkeit mal genauer an.
Wie der Name sagt, ist die Lichtgeschwindigkeit eine Geschwindigkeit. Diese ist definiert als \frac{Länge}{Zeit}. Welcher Zahlenwert die Lichtgeschwindigkeit hat ist rein willkürlich. Wir haben die Angabe von einem Meter und einer Sekunde festgelegt und damit den Wert der Lichtgeschwindigkeit. Da man allgemein von der Konstanz der Lichtgeschwindigkeit überzeugt ist, macht man in der Physik die Definition umgekehrt. Die Lichtgeschwindigkeit wird festgelegt und es ergibt sich daraus eine Definition von Meter und Sekunde. Aus Sicht der DP kann man die Lichtgeschwindigkeit sehr einfach festlegen. Dies ist die Geschwindigkeit, bei der die Zeitdilatation und die Längenkontraktion null erreichen. Damit ist die maximale Verformung der Raumzeit für eine Raumzeitdichte erreicht.
Warum erhalten wir einen konkreten Wert für die Lichtgeschwindigkeit. Es müsste dann doch \frac{Länge\space =\space 0}{Zeit\space =\space 0} für das Objekt sein. Das ist ein nicht definierter mathematischer Ausdruck und kein konkreter Zahlenwert. Zum Glück hat unserer Raumzeit mehr als eine Raumdimension. Die Abbildung der Raumzeitdichte eines Objektes, welches sich mit Lichtgeschwindigkeit bewegt, darf daher nur auf den anderen zwei Raumdimensionen vorhanden sein. Dort muss eine Raumzeitdichte abgebildet sein. Das ist aber noch nicht ausreichend. Wir können nur eine Raumzeitdichte als Objekt feststellen. Zwei Raumdimensionen ergeben keine Raumzeitdichte. Das Objekt (z.B. ein Photon) muss ein weiteres Merkmal trage, damit wir dies erkennen können. Das erklären wir noch in diesem Kapitel, aber in einem späteren Abschnitt.
Wir Wissen bereits, dass die Planck-Länge und die Planck-Zeit die Lichtgeschwindigkeit definieren. Aus der Definition heraus, gibt es aber unendlich viele Werte für die Länge und die Zeit. Die Geschwindigkeit ist ein Bruch. Es könnte auch z.B. nur die halbe Planck-Lange und halbe Planck-Zeit sein. Diese Grenzbedingung allein setzt explizit nicht Planck-Zeit und Planck-Länge als kleinstmögliche Länge- und Zeiteinheit in der Raumzeit fest. Es ist die Kombination, also der Bruch, was die Lichtgeschwindigkeit ausmacht. Das für uns wichtige Ergebnis ist, es gibt Objekte, welche in unserer Raumzeit, auf dieser Grenze noch vorhanden sind. Damit existiert diese Grenze für uns.
Die Lichtgeschwindigkeit ist ein Strukturelement der Raumzeit
Es gibt kein Grund für ein Postulat der Lichtgeschwindigkeit als maximale Geschwindigkeit. Der zweite Teil des Postulates, die Konstanz für jeden Beobachter, werden wir beim Relativitätsprinzip besprechen. Die Grenze als maximale Geschwindigkeit für (fast) alles im Universum ergibt sich automatisch aus dem Ansatz der Raumzeitdichte. Da alles, was existiert eine Raumzeitdichte ist, ist jedes Objekt davon betroffen.
Ein Beobachter erkennt (z.B. für ein Photon), eine Bewegung der Raumzeitdichte in Bewegungsrichtung mit seiner Zeit exakt auf dieser Grenze. Für die Raumzeitdichte, welche sich mit Lichtgeschwindigkeit bewegt, besagt diese Definition etwas anderes aus. Existiert ein Objekt, dass seine Raumzeitdichte nur auf zwei Raumdimensionen abgebildet hat, dann kann dieses Objekt unsere 3D Raumzeit nicht wahrnehmen. Eine Raumdimension muss explizit fehlen. Aber nicht nur eine Raumdimension. Es fehlt auch die Zeitdimension. Diese geht wie die Raumdimension gegen null. In der bisherigen Auslegung dieser Gegebenheit hat man drin keine Besonderheit gesehen. Für uns ist dies anders.
Eine der größten Innovation von Einstein war es Raum und Zeit zu einem einzigen Objekt der Raumzeit zu vereinen. Nur so konnte die SRT und später die ART funktionieren. Wir nehmen diesen „Einheitsgedanken“ zur Raumzeit zu 100% ernst und übertragen dies auf die Lichtgeschwindigkeit. Wollen wir unsere Raumzeit verlassen, dann muss die Zeitdilatation auf null gehen. Die Zeit ist zwingender Bestandteil der Raumzeit. Eine Zeitdilatation auf null haben wir bei der Lichtgeschwindigkeit. Nun macht das Verhalten der Raumzeitkomponenten Sinn. Durch die Längenkontraktion wird eine Raumdimension immer „weniger oder besser dichter“.
Wir verändert die Raumzeitkonfiguration in Richtung von (-, +, +, +) zu (-, +, +). Dabei geht die Zeitdimension durch Zeitdilatation auch gegen null und das Ergebnis ist (+, +). Dies ist keine Raumzeit mehr. Es ist keine Zeitdimension vorhanden. Wir haben damit unsere Raumzeit verlassen. Aus dieser Überlegung holen wir unsere wichtigste Schlussfolgerung:
Unsere und damit alle Raumzeiten haben Grenzen.
Diese Grenzen, separat je Raumzeit, können wir dadurch definiert, dass die Zeitdimension gegen null gehen muss.
Eine dieser Grenzen kennen wir bereits, die Lichtgeschwindigkeit. Diese ist die niederdimensionale Grenze. Durch die Längenkontraktion verlieren wir bei der Lichtgeschwindigkeit eine Raumdimension. Damit verändern wir die Raumzeitkonfiguration der Raumzeit und gehen aus unserer Raumzeit heraus. Hier ist der Punkt, wo die Analogie mit einer Substanz falsch ist. Wenn man die Eigenschaften einer Substanz oder eines Objektes verändert, dann ist es immer noch das Objekt. Nur mit anderen Eigenschaften. In der Raumzeit ist es anders. Verändern wir die Raumzeitkonfiguration, mit einer Raumdimension mehr oder weniger, dann wird die Zeitdimension zwingend auf null gesetzt und wir verlassen die Raumzeit.
Dann ist z.B. ein Photon ein echtes Schnittstellenobjekt unserer Raumzeit. Es liegt direkt auf der Grenze der Raumzeit. Nur weil die Abbildungen der Raumzeitdichte auf den anderen zwei Raumdimensionen vorhanden ist, können wir diese Objekte überhaupt erkennen. Dann aber, wenn keine Wechselwirkung vorliegt, nur im Zustand der Lichtgeschwindigkeit. Dies ist für ein Photon die Existenzbedingung und nicht einfach eine Geschwindigkeit.
Mich persönlich erfreut die Erkenntnis sehr, dass die Raumzeit Grenzen hat und eine davon die Lichtgeschwindigkeit ist. Vor langer, langer Zeit, als ich am Wirtschaft Gymnasium war, hatte ich einen Physiklehrer, Herrn Werner. Dieser erfüllt zu 100% alle Vorurteile und Klischees für einen Mathematik- und Physiklehrer. Leider verstarb Herr Werner noch zu meiner Zeit an dieser Schule. Gegen Ende des ersten Schuljahres saß ein Teil der Klasse bei einem Bierchen an Lagerfeuer. Mir ist es wichtig zu betonen, dass so etwas nicht im Schulunterricht passiert ist. Da ich schon Interesse an Physik hatte, fragte ich Herrn Werner wie er denn zum Physikstudium gekommen ist und er dies empfand. Er ist mit der QM nicht so richtig warn geworden, empfand aber die ART als sehr elegant und schön. Er hatte aber mit einer Stelle ein Problem. Dies war nicht die Singularität in der ART, sondern die maximalle Geschwindigkeit. Relativitäts- und Äquivalenzprinzip erschienen Ihm logisch und einfach nachvollziehbar. Ihm war klar, dass dies alles nur funktioniert, wenn es dies maximale Geschwindigkeit gibt. Das Postulat der Lichtgeschwindigkeit ist Ihm aber als „Fremdkörper“ in der Theorie vorgekommen. Dafür würde er gerne eine logische Erklärung haben.
Diese Fragestellung von Herrn Werner ist mir seit diesem Abend nicht mehr aus dem Kopf gegangen und ist einer der Hauptgründe, warum es die DP gibt. Mit dem Ansatz der Raumzeitdichte und der Raumzeit als Objekt/Substanz, ist dies Fragestellung geklärt. Die Lichtgeschwindigkeit ist keine festgelegte Geschwindigkeitsgrenze. Diese ergibt sich zwingend aus dem Ansatz. Es gibt keinen „höheren“ Bewegungszustand als die Lichtgeschwindigkeit. Die Zeit- und Raumdimension ist null. Weniger geht nicht. Man muss die Definition der Lichtgeschwindigkeit umdrehen. Nicht bei Lichtgeschwindigkeit werden die Zeitdilatation und die Längenkontraktion null. Das Erreichen der niederdimensionalen Grenze unserer Raumzeit ist die Bedingung für die Definition der Lichtgeschwindigkeit.
Die niederdimensionale Grenze ist die Lichtgeschwindigkeit
Schön, dass ich mit der niederdimensionalen Grenze meinen persönlichen Frieden gefunden habe. Bringt uns diese Erkenntnis an andere Stelle weiter? Wenn ich schon so Frage, ja. Die niederdimensionale Grenze oder Lichtgeschwindigkeit, kann als identische Bezeichnung gewählt werden und erklärt den harten Schalter zwischen Objekten mit oder ohne Ruhemasse und was Energie oder Masse überhaupt ist.
Wenn wir uns der niederdimensionalen Grenze nähern, geht die Raumzeitdichte gegen unendlich. Das identische Verhalten kennen wir von der Energie. Das ist kein Zufall. In der DP setzten wir die Raumzeitdichte und Energie gleich. Das sollte durch den Ansatz klar sein. Wir setzen die Raumzeitdichte als Quelle der Raumzeitkrümmung fest. Die Quelle einer Raumzeitkrümmung ist jegliche Form von Energie. Daher muss sich die Identität zwischen Energie und Raumzeitdicht zwingend ergeben. Damit können wir aber erklären, was Energie ist. Energie ist eine andere Angabe für die geometrische Definition der Raumzeit selbst.
Energie ist eine identische Angabe zur geometrischen Definition der Raumzeit = Raumzeitdichte
Wir haben hier zwei verschiedene Brillen oder Maßeinheiten für eine identische Aussage. Um diese Betrachtung weiter zu vertiefen, holen wir uns die bekannteste Formel von Einstein:
E\space =\space mc^2
Die Formel ist richtig. Sie ist aber nur so bekannt, weil die Formel in dieser Form sehr einfach ist. Die vollständige Formel hatte nie die Chance so bekannt zu werden, da diese etwas komplizierter ist:
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
Wenn der zweite Term unter der Wurzel null ist, können wir die Wurzel ziehen und landet wieder bei dem bekannten Teil, der Ruhemasse. Damit der zweite Term null ist, muss die Bewegung, also der Impuls mit p^2 unbedingt null sein. Die Lichtgeschwindigkeit c ist konstant und kann nicht null sein
Der erste Term entspricht der Ruhemasse. Auf diese gehen wir jetzt nicht näher ein. Dazu müssen wir die Grenzen der Raumzeit vollständig verstanden haben. Die Beschreibung der Ruhemasse kommt daher am Ende des Kapitels.
Der für uns jetzt interessante Teil bei der Ruhemasse sind zwei uralte bekannte Sachen.
Damit lassen wir die Ruhemasse bis zum Ende des Kapitels ruhen.
Wir wollen den zweiten Term betrachten, den Impuls. Bei unserem Ansatz muss der Impuls eine direkte Abbildung in der Raumzeitgeometrie haben. Das Ganze mit einer Richtung. Das bedeutet für uns, dass es eine Raumzeitdichte mit einer ausgezeichneten Richtung geben muss.
Für den umgangssprachlichen Begriff der Dichte klingt eine ausgezeichnete Richtung etwas seltsam. In einem Gas oder einer Flüssigkeit ist die Dichte in allen Richtungen identisch. Für die Raumzeit ist dies anders. Hier haben wir nur die Definition der Geometrie für eine Beschreibung. Die Raumzeitdichte liegt immer auf der Zeitdimension und auf mindestens einer Raumdimension. Für eine Dichte in Raum und Zeit, muss mindestens eine Raumdimension und eine Zeitdimension beteiligt sein. Die Raumzeitdichte muss nicht zwingend auf allen Raumdimensionen abgebildet werden. Wir brauchen mindestens eine Raumdimension, sonst macht der Begriff eine Raumzeitdichte keinen Sinn. Es können daher in verschiedenen Raumdimensionen unterschiedlich starke Dichten vorliegen. Damit ist ein Impuls ein Raumzeitdichte mit einer in mindestens einer Raumdimension ausgezeichneten Richtung. Beim Drehimpuls wird die Richtung ständig geändert, was eine ständige Veränderung der Geometrie bedeutet. Dies können wir feststellen, da eine „interne Kraft“ das Objekt z.B. einen Stern, gegen diese Veränderung der Richtung zusammenhalten muss. Die Raumzeitdichte nimmt aber nicht ab, wenn diese an Ort und Stelle bleibt oder in der Raumzeit eine Verschiebung erfährt. Diese wird nur auf eine andere „Richtung/Raumdimension“ verschoben. In Summe wird aber nichts verändert.
Bisher haben wir die Energie und die Geometrie der Raumzeit gleichgesetzt. Nun ist der Impuls oder Drehimpuls auch eine Form der Energie. Damit muss es für die Definition der Geometrie zwei verschiedene Beschreibungen geben. Eine vektorielle Dichte als Impuls und eine skalare Dichte als Ruhemasse. So einfach geht dies aber nicht. Wenn die Raumzeitdichte einen Bewegungszustand kennzeichnet, dann muss auch die Ruheenergie einen Bewegungszustand haben. Wie der Name sagt, ist dies bei der Ruhemasse nicht der Fall. Ok, aber wohin zeigt dann die Bewegung für eine Ruhemasse. In allen Richtungen gleichzeitig. Dann heben sich die Bewegungen gegenseitig auf und die Ruhemasse hat sich ihren Namen verdient. Wir werden im Kapitel Kosmologie sehen, dass dies zum Beispiel bei der Raumzeitexpansion der Fall ist. Bei einem Teilchen mit Ruhemasse, muss diese Masse daher aus der niederdimensionalen Schnittstelle kommen, sonst würde sich in unserer Raumzeit die Raumzeitdichte zu null aufheben. Damit muss im Umkehrschluss der Impuls immer in unserer Raumzeit liegen. Dies bedeutet, der erste Term für die Energie kommt aus der niederdimensionalen Schnittstelle und der zweite Term liegt direkt in unserer Raumzeit. Wir ziehen die Definition für die Raumzeitdichte immer enger. Hier können wir folgende Bedingung festsetzen:
Raumzeitdichte ist Energie, Geometrie der Raumzeit und Bewegungszustand
Raum und Zeit wurden zu einer Raumzeit vereint. Dies müssen wir auch für diese Begriffe machen. Diese Begriffe sind jeweils unterschiedliche Beschreibungen eines einzigen Objektes, der Raumzeitdichte.
Noch ein Wort zur Bewegung. Das der Bewegungszustand eines Objektes, eine Geometrie in der Raumzeit des Objektes selbst ist, dürfen wir ohne Einschränkung als, sagen wir mal, ungewöhnlich bezeichnen. Daran müssen wir uns erstmal gewöhnen. Verändern sich nicht alle Raumdimension identisch, so erhält man eine Bewegung im Raum. Das, was wir umgangssprachlich als Bewegung beschreiben. Verändern sich alle Raumdimensionen identisch, dann ist dies eine Veränderung als Ruhemasse oder das Gegenstück, die Raumzeitexpansion. Bei der Raumzeitkrümmung, mit gegenläufiger Veränderung der Komponenten wird dadurch die Bewegung im Raum verändert und wir erhalten das „Äquivalenzprinzip“. Dazu gibt es ein separates Kapitel. Die Unterschiede werden an der jeweiligen Stelle nochmals erklärt.
Aus unserem Ansatz heraus sollte der Umstand, dass wir die Bewegung direkt in der Geometrie der Raumzeit verankern, nicht verwundern. Die Raumzeit besteht nur aus Länge und Zeit. Damit muss die Raumzeit eine Darstellung von Geschwindigkeit sein. Eine andere physikalische Größe lässt sich mit nur Länge und Zeit nicht aufbauen.
Mit dem bisherigen Bild der Raumzeitdichte ist es sehr einfach zu erklären, warum es Objekte mit Ruhemasse und einem Bewegungszustand unterhalb der Lichtgeschwindigkeit und Objekte ohne Ruhemasse und dem exakten Bewegungszustand der Lichtgeschwindigkeit gibt.
Bei einem Objekt mit Ruhemasse, z.B. ein Elektron muss die Raumzeitdichte alle 3 Raumdimensionen unserer Raumzeit belegen. Die Lichtgeschwindigkeit ist die niederdimensionale Grenze der Raumzeit. Unserer Raumzeit verliert dann eine Raumdimension. Eine gegebene Raumdimension kann nicht einfach verschwinden. Diese kann nur bis zur Lichtgeschwindigkeit immer weiter eine steigende gerichtete Raumzeitdichte erhalten. Die gegebene skalare Raumzeitdichte, zum Beispiel die Ruhemasse für ein Elektron, wird immer weiter in Bewegungsrichtung verdichtet. Damit erhält man eine bis ins Unendliche steigende Energie. Daher ist das erreiche der Lichtgeschwindigkeit ausgeschlossen.
Raumzeitdichte mit Ruhemasse = 3 Raumdimensionen sind belegt
Ein Objekt ohne Ruhemasse darf auf keinen Fall alle 3 Raumdimensionen belegen. Es darf nur zwei Raumdimensionen belegen. Damit fehlt eine Raumdimension bereits auf Grund des „inneren Aufbaus“ des Objektes. Das Objekt darf keine Beschleunigung erfahren. Es muss sich bereits ab seiner Existenz mit Lichtgeschwindigkeit bewegen. Ein anderer Bewegungszustand ist ohne Wechselwirkung nicht möglich. Das Objekt lebt in der niederdimensionalen Schnittstelle unserer Raumzeit.
Raumzeitdichte ohne Ruhemasse = 2 Raumdimensionen sind belegt
Aus diesen Punkt lässt sich eine Prüfung für die DP erzeugen. Wird für ein Objekt ohne Ruhemasse jemals eine Beschleunigungsphase zur Lichtgeschwindigkeit entdeckt, ist die DP falsifiziert.
Aber, aber! Die Wechselwirkung mit den Higgs-Feld, über das Higgs-Boson gibt doch den Teilchen die Ruhemasse? Nicht ganz richtig! Dies können wir etwas anders sehen. Das Higgs-Feld muss in der DP irgendeiner Form einer 3D Raumzeit entsprechen. Das Higgs-Boson, muss in unserer Sichtweise ein Austauschteilchen zwischen mehreren solcher „Higgs-Felder“ sein. Das werden wir im Teil 3 klären.
Damit ist klar, dass ein Objekt entweder das eine oder das andere ist. Nur in einem „Umwandlungsprozess (Wechselwirkung in der QM)“ des Objektes, kann sich die „Innere Struktur (Standardmodell der Teilchenphysik)“ verändern. Die Raumzeitdichte kann sich auf die Raumdimensionen neu verteilen.
Da bei Lichtgeschwindigkeit, die Raum- und die Zeitdimension bereits auf null ist, kann nicht noch eine Raumdimension auf null gehen. Die Lichtgeschwindigkeit kann nur eine Richtung haben. Aus diesen Punkt lässt sich eine Prüfung für die DP erzeugen. Kein Objekt darf in zwei Richtungen gleichzeitig die Lichtgeschwindigkeit aufweisen. Wir können die Zeitdimension nur einmal auf null setzen.
Wir können aus der Lichtgeschwindigkeit, die wir mit der niederdimensionalen Grenze gleichsetzen, folgende Bedingungen ableiten:
Es gibt mit der Lichtgeschwindigkeit eine niederdimensionale Grenze. Gibt es dann auch eine höherdimensionale Grenze? Eine Raumzeit mehr und nicht weniger. Die Bedingung, um die Raumzeit zu verlassen ist, die Zeitdilatation gegen null. Diese gibt es im Universum an nur zwei Stellen.
Die Bedingung, die zu einem Schwarzen Loch führt, muss die höherdimensionale Grenze sein. Diese Bedingung ist uns sehr gut bekannt. Wenn man zu viel Raumzeitdichte (Energie) auf eine zu kleine Länge unterbringt, geht es ab ins Schwarze Loch.
Diese Bedingung ist, mit den konkreten Werten, bereits bekannt. Es ist der Kehrwert der Planck-Kraft. Das ist als Bezeichnung und in der Maßeinheit als Kraft für eine Erklärung sehr umständlich zu handhaben. Daher werden wir diesen Grenzwert anders Definieren und einen passenderen Namen wählen. Das machen wir wie bei der Raumzeitdichte.
Kraft souveräner Willkür => Dimensionale Konstante mit der Abkürzung d.
Damit hat die höherdimensionale Grenze eine klare Bezeichnung. Den Teil „höher“ lassen wir bei der Dimensionalen Konstante weg. Der Name Lichtgeschwindigkeit ist in allen Gehirnen vollständig eingebrannt. Diesen können wir nicht mehr verändern. Die niederdimensionale Grenze kann daher mit der Dimensionalen Konstante nicht gemeint sein. Die Dimensionale Konstante ist wie die Lichtgeschwindigkeit eine der wichtigsten Naturkonstanten in unserer Raumzeit. Diese ist ebenso ein Strukturelement der Raumzeit und kein festgelegter Wert.
Die Leichtgeschwindigkeit ist mit c\space =\space \frac{Länge}{Zeit} festgelegt. Bei der Dimensionalen Konstante ist es:
d\space =\space \cfrac{Länge}{Energie}
Wenn wir zu einer Kraft eine Länge dazu nehmen (andere Brille aufsetzen), erhält man die Einheit Energie. Daher muss bei einem Kehrwert der Kraft der Bruch im Nenner und im Zähler um eine Länge erweitert werden. Diese Darstellung ist für Erklärungen besser geeignet und wird deshalb als Definition verwendet.
In beiden Fällen macht es Sinn eine Länge in der Definition zu haben. Eine Raumzeitdichte braucht immer eine Raumdimension, um sich überhaupt in der Raumzeit abbilden zu können. Beide Grenzen sind Brüche, da es jeweils Aufteilungen zu einer Länge sind. Die Länge steht im Zähler, weil wir eine Länge in der Zeit oder der Energie unterbringen müssen, damit eine Raumzeitdichte Sinn macht. Dies wird ein generelles Prinzip werden. Die Definition einer Naturkonstante für unsere Raumzeit muss immer eine Länge beinhalten.
Da die Dimensionale Konstante wieder ein Bruch ist, gilt hier die identische Aussage wie bei der Lichtgeschwindigkeit. Die Länge und die Energie legen keine kleinste Länge oder eine größte Energie fest. Es kann wieder halbe Planck-Länge und Planck-Energie sein. Nur die Kombination der Werte ergibt die Dimensionale Konstante.
Die Werte sind uns wiederum als Planck-Werte bekannt. Rein aus der Lichtgeschwindigkeit und der Dimensionalen Konstante können wir die Werte nicht festlegen. Das sind 2 Gleichungen mit 3 Unbekannten. Da fehlt noch eine Angabe. Die fehlende Angabe werden wir uns noch in diesem Kapitel verschaffen.
Wenn man der Dimensionalen Konstante eine Analogie geben will, dann ist dies wohl ein Wert für einen Widerstand der Raumzeit gegen die Raumzeitdichte. Wird dieser Wert überschritten, so ist die Raumzeitdichte für unsere Raumzeit zu hoch. Die Raumzeit muss in einen Bereich gehen, der diesen Wert aushält. Dies kann nur eine Raumzeit mit einer Raumdimension mehr sein. Eine Raumzeit mit n+1 Raumdimensionen lässt sich schwerer verformen als eine Raumzeit mit n Raumdimensionen. Dieses Prinzip werden wir noch im Teil 3 für die QM benötigen.
Dabei ist bereits unsere Raumzeit ein verdammt zähes Stück. Kleine Berechnung (Achtung! Alle Werte für die Planck-Einheiten sind nicht reduziert, also nicht durch 2\pi gekürzt):
Planck-Länge =\space l_P\space =\space 4,051\space *\space 10^{-35} Meter
Planck-Zeit =\space t_P\space =\space 1,351\space *\space 10^{-43} Sekunden
Plankc-Masse =\space m_P\space =\space 5,455\space *\space 10^{-8} Kilogramm
Planck-Energie =\space m_P\space *\space c^2\space =\space 4,903\space *\space 10^9 Joule
d\space =\space \cfrac{l_P}{E_P}\space =\space 8,262\space *\space 10^{-45} 1/Newton
\cfrac{1}{d}\space =\space 1,210\space *\space 10^{44} Kehrwert von d, Newton
Egal mit welcher Raumzeitdichte wir eine Raumzeitkrümmung auslösen wollen. Die Raumzeitkrümmung ist um diesen Faktor geringer. Da müssen wir sehr viel Energie auf einer kleinen Länge unterbringen, damit dieser Wert überbrückt werden kann. Dies ist die Bedingung, die zu einem Schwarzen Loch führt. Da uns c mit der Planck-Länge und Planck-Zeit bekannt ist, kommt hier als neuer Wert nur die Planck-Masse dazu. Die Planck-Energie wird ausgerechnet. Damit bestimmen diese drei Planck-Werte die Grenzen der Raumzeit. Hier müssen wir wieder die Definition umdrehen. Die Grenzen der Raumzeit bestimmen diese drei Planck-Werte und sind damit charakteristische Werte für unsere Raumzeit.
Planck-Länge, -Zeit und -Masse sind für unsere Raumzeit charakteristische Werte
Ein Schwarzes Loch ist der Übergang in eine höherdimensionale Raumzeit, welche diese Raumzeitdichte abbilden kann. Dann muss im Umkehrschluss eine niederdimensionale Raumzeit eine kleinere Planck-Masse haben. Diese unterschiedlichen Planck-Massen je niederdimensionale Raumzeitkonfiguration werden später im Standardmodell der Teilchenphysik die unterschiedlichen Ruhemassen der Teilchen sein.
Jede Raumzeitkonfiguration hat seine eigenen Planck-Werte für die Planck-Einheiten
Machen wir noch eine kleine Gegenrechnung. Wenn wir d als maximalen Widerstand der Raumzeit ansehen, dann müssten wir dies auf einfachen Weg berechnen können. Wie nehmen die Formel von Newton für die Gravitationskraft mit:
F\space =\space \cfrac{g\space *\space m_1\space *\space m_2}{r^2}
Wenn wir für dies Formel die extremen Werte für Masse (Planck-Masse) und Abstand (Planck-Länge) einsetzen, dann muss unser maximaler Wert auch erscheinen. So ist es auch. Der Grund wird später, wenn wir die Naturkonstanten besprechen, klarer werden. Wenn eine Aussage zur Physik stabil sein soll, so kommen wir oft auf verschiedenen Wegen zu dieser Aussage. Das ist immer ein gutes Zeichen für die Richtigkeit.
F_{max}\space =\space \cfrac{g\space *\space m_P\space *\space m_P}{l_P^2}\space =\space 1,210\space *\space 10^{44}
In der Physik gibt es das sogenannte Hierarchieproblem. Dies ist ein Name für die große Differenz, wenn man die Gravitation als Kraft mit der elektromagnetischen Kraft vergleicht. Das haben wir schon ganz am Anfang gemacht. Der Wert: 4\space *\space 10^{42}
Dies ist ein sehr großer Unterschied in der Betrachtung als Kraft. Das können wir aber leicht erklären. Alle Grundkräfte aus der QM liegen immer im niederdimensionalen. Da wollen wir später die gesamte QM abbilden. Laut unserer Logik muss sich eine niederdimensionale Raumzeit sehr viel leichter verformen lassen als unserer Raumzeit. Wie wir sehen können, ist der Unterschied in dem Widerstand der jeweiligen Raumzeit sehr groß.
Wir wiederholen die Rechnung, aber nicht mit der Ruhemasse eines Elektrons m_e, sondern mit der Planck-Masse m_P. Wir tun mal so, als ob eine 2D-Raumzeit die identischen Planck-Werte wie unserer 3D-Raumzeit hätte. Dann ergibt sich nur noch ein Unterschied von 0,00116140. Dieser Wert ist uns als die Feinstrukturkonstante α bekannt. Allerdings nur, wenn wir α um 2\space *\space \pi kürzen. Das war der zusätzliche Term, den wir beim Vergleich von elektrischer zu gravitativer Kraft benutzt haben. Diese 2\space *\space \pi werden ums gleich nochmals begegnen Die Kräfte wären dann bis auf α identisch. Die Feinstrukturkonstante besprechen wir in Teil 3.
Das Hierarchieproblem ist einfach der große Unterschied im Widerstand der Raumzeitkonfigurationen, wenn man eine Raumdimension mehr oder weniger hat.
Die beiden Grenzen der Raumzeit haben wir gefunden, weil wir uns die Extreme der Raumzeit angeschaut haben und es war doch schon immer eine der großen Fragen: „Wie soll man sich null oder unendlich vorstellen“. Mathematisch hat man diese Begriffe inzwischen recht gut im Griff. Physikalisch kommt man damit immer wieder auf „schräge“ Gedanken. Wir wollen dies eindeutig klären. Das Ergebnis wird sein, dass es innerhalb einer einzigen Raumzeit bei den Verformungen weder ein Wert von null noch unendlich vorkommen kann.
Die Raumzeitdichte ist eine Dichte der Raumzeit selbst. Eine Raumzeitdichte von null bedeutet damit gleichzeitig auch eine nicht existierende Raumzeit. Schauen wir uns das genauer an. Bei unserem Ansatz ergibt sich eine Raumzeitdichte bereits durch die Existenz mindestens einer Raum- und Zeitdimension. Ohne einer Raumdimension kann es eine Abbildung als Dichte nicht geben. Dies bedeutet für uns, dass es einen Raumzeitpunkt, mit der Raumzeitdichte von null, nie geben kann. Dieser Raumzeitpunkt beinhaltet dann keine Ausdehnung auf einer Raumdimension und ist damit überhaupt kein Teil der Raumzeit.
Wir haben den Begriff „Raumzeitpunkt“ verwendet. Das werden wir auch weiterhin. In der Physik wird oft mit einer Punktgröße gearbeitet und gerechnet. Das vereinfacht die Vorstellung und insbesondere die Berechnungen. Wer bis zu diesem Zeitpunkt aufmerksam mitgelesen hat, sollte aber folgende Erkenntnis gewonnen haben:
In der DP gibt es keinen Punkt
Die mathematische Abstraktion eines Punktes, ist dadurch definiert, dass ein Punkt explizit in keine Raumdimension eine Ausdehnung besitzt. Damit ist dieser nicht Teil der Raumzeit. Er kann keine Raumzeitdichte aufweisen. Damit auch keine Definition der Raumzeitgeometrie, keine Energie und keinen Bewegungszustand. Wann immer von einem Raumzeitpunkt, einer Punktmasse usw. gesprochen wird, dies ist eine reine mathematische Abstraktion, um das Problem oder die Berechnung zu vereinfachen. In der DP kann es eine Punktgröße, egal welcher Art, nicht geben. Wir drehen die Argumentation um. Nicht die ART oder die QM haben Probleme bei einer Punktgröße, sondern die mathematische Abstraktion eines Punktes hat in der Physik keine reale Abbildung.
Wir haben nur die Raumzeitdichte betrachtet. Wie sieht es denn bei der Raumzeitkrümmung aus? Kann die Gravitation denn null werden? Aus dem, was wir bisher besprochen haben, theoretisch ja. Dazu brauchen wir eine Raumzeit mit einer absoluten homogenen Raumzeitdichte. Wenn es von Raumzeitpunkt (wir verwenden diese Abstraktion weiterhin) zu Raumzeitpunkt keine Differenz in der Raumzeitdichte gibt, dann gibt es auch keine Raumzeitkrümmung, die irgendetwas ausgleichen muss.
Wir leben aber in einer Raumzeit mit unterschiedlichen Raumzeitdichten, sonst könnten wir hier nicht diskutieren. Die Raumzeitkrümmung hat eine unendliche Reichweite. Gibt es auch nur eine abweichende Raumzeitdichte, dann gibt es auch eine Raumzeitkrümmung. Damit ist klar, in unserem Universum ist immer eine Raumzeitkrümmung vorhanden.
Hier gibt es noch keine zwingende Grenze. Die Lichtgeschwindigkeit besagt aus, dass man bis zur niederdimensionalen Grenze eine unendliche Menge an Energie benötigt. Bekommen wir diese den irgendwoher? Klares nein. Hier drei Argumente:
Egal von welcher Seite wir auch kommen. Eine einzelne Raumzeit lässt keine unendliche Raumzeitdichte oder Raumzeitkrümmung zu.
Der ART wird oft angekreidet, dass diese im Urknall oder im Zentrum eines Schwarzen Loches eine Singularität voraussagt. Dies ist nur richtig, wenn man die Raumzeitdichte auf eine Punktgröße zurückführt oder anders ausgedrückt, unsere Raumzeitgrenzen nicht kennt. Beim Urknall die gesamte Raumzeit, beim Schwarzen Loch die Masse dieses Objekts. In beiden Fällen ist dies aber nur eine mathematische Abstraktion. Leider ist in der Feldgleichung der ART dieser Umstand nicht enthalten. Im Einstein-Tensor kann man eine Raumzeitkrümmung bis ins unendliche bringen, wenn man für die Raumzeitdichte eine Punktgröße annimmt. Dann müsste aber die Raumzeitdichte weg sein. Ein Schwarzes Loch in unserer Raumzeit hat immer eine Masse. Das Schwarze Loch ist da, damit auch die Raumzeitdichte, welche zu diesem geführt hat. Damit ist im Zentrum eines Schwarzen Loches immer ein Volumen an Raumzeitdichte erhalten.
In der DP gibt es keine Singularität
Die Abstraktion eines Punktes hat schon immer für Probleme gesorgt. Der Ansatz der Stringtheorie kommt genau daher. Keine Punkt, sondern die erste mathematische „Stufe“ über dem Punkt, ein Objekt mit nur einer Raumdimension, ein String.
Damit haben wir, in Summe für eine Raumzeit, ein sehr schönes Ergebnis. Für die Raumzeitdichte kann es bereits theoretisch keinen Wert von null oder unendlich geben. Bei der Raumzeitkrümmung kann es eine unendliche Raumzeitkrümmung bereits theoretisch nicht geben. Leider ist dies nicht in den Feldgleichungen enthalten. Es könnte eine Raumzeitkrümmung von null geben, dann gibt es in dieser Raumzeit aber keine abweichende Raumzeitdichte und ist damit „leer“. Mit leer ist hier gemeint, dass es keine Teilchen geben darf. Die Raumzeit selbst trägt auch ohne ein Teilchen eine Energie. Dazu reicht die Existenz aus.
Wir schauen uns die bisher verwendeten Naturkonstanten und Planck-Werte genauer an. Dann holen wir uns noch das Planck’sche Wirkungsquantum h dazu, damit wir unseren drei, bis jetzt nicht bestimmten Planck-Werte Länge, Zeit und Masse, mit einer weiteren Gleichung festlegen können. Hier gibt es einen kleinen Vorgriff auf den Teil 3. Wir besprechen gleich noch die Compton-Wellenlänge mit. Wir werden erkennen, dass das Wirkungsquantum und die Compton-Wellenlänge aus der niederdimensionalen Grenze unserer Raumzeit folgt und nicht im niederdimensionalen (QM) bestimmt wird. Die ART gibt der QM dieses Verhalten vor und nicht umgekehrt.
In den Lehrbüchern sind die drei wichtigsten Naturkonstanten immer c, h und G. In der DP werden wir dies zu c, h und d verschieben. Dann darf für uns die Gravitationskonstante G keine weitere Relevanz mehr haben. Das erreichen wir, da G sich aus c und d zusammensetzt. Es macht Sinn, dass die Gravitationskonstante G sich aus den Grenzen der Raumzeit erzeugt. Das Verhalten der Raumzeit in der klassischen Sicht mit G, muss zwischen den Grenzen der Raumzeit liegen. Diese Grenzen sind bis jetzt die einzigen, durch unsere Raumzeit festgelegten Werte.
Da G eine Naturkonstante ist, hat diese noch keine Herleitung erfahren. Das Wort „Naturkonstante“ bezeichnet einfach, dass man in der Physik bei einer Formel eine Proportionalitätskonstante benutzt, über die man kein Wissen hat. Keine Erklärung dafür heißt, Naturkonstante. Wir konnten c und d aus den dimensionalen Grenzen unserer Raumzeit herleiten. Wenn G keine Naturkonstante mehr sein soll, müssen wir G aus bekannten (und ganz wichtig, hergeleiteten) Naturkonstanten erzeugen können.
Da wir schon mit den Planck-Einheiten arbeiten, machen wir hier weiter. Die Gravitationskonstante wird über die Planck-Einheiten, wie folgt definiert: G\space =\space \frac{l_P^2\space *\space c^3}{h}
Wir greifen etwas vor und legen fest, dass wir das Planck’sche Wirkungsquantum h\space =\space l_P\space *\space m_P\space *\space c schreiben können. Damit erhalten wir G\space =\space \frac{l_p\space *\space c^2}{m_P}. Diesen Bruch erweitern wir um c^2. Dann haben wir die gewünschte Form:
G\space =\space \cfrac{l_P}{E_P}\space *\space c^4\space =\space d\space *\space c^4
Die Gravitationskonstante ist aus c und d zusammengesetzt. Wir können auch erklären, warum c und d so verwendet werden müssen. Das bedeutet, wir müssen erklären können, warum d ohne Exponenten verwendet wird und c den Exponenten 4 haben muss.
Die Dimensionale Konstante d erzeugt ein Schwarzes Loch und damit die höherdimensionale Grenze für die gesamte Raumzeit. Egal auf welcher Raumdimension die Raumzeitdichte abgebildet wird. Ist d auf einer beliebigen Dimension erreicht, dann erzeugt sich ein Schwarze Loch für die gesamte Raumzeit. Daher wird kein Exponent benötigt.
Die Lichtgeschwindigkeit c ist für jede Raumdimension unabhängig. Der Impuls in eine Richtung, beeinflusst nicht die anderen Raumdimensionen. Längenkontraktion ergibt sich nur in Bewegungsrichtung. Daher muss für die Betrachtung der gesamten Raumzeit unbedingt ein c^4 verwendet werden. Aber, die Zeitdimension geht doch immer mit einer Raumdimension mit. Wieso nicht eine 3 als Exponent? Das kommt durch den Aufbau der Feldgleichungen für die ART. Das zeigen wir im nächsten Abschnitt.
Damit haben wir doch nur eine Verschiebung von c und G auf c und d erreicht. Austausch eines Buchstabens und fertig. Klares nein! Die Existenz der Konstanten c und d können wir auf Grund unseres Ansatzes herleiten. Für G gibt es keine Erklärung. Bei uns ist G dann einfach die passende Kombination aus c und d, wenn man eine Aussage innerhalb der Raumzeit treffen will. Wir sehen im nächsten Abschnitt, dass die Verwendung von G in der Feldgleichung gar nicht sinnvoll ist.
Holen wir uns noch einmal die Feldgleichung der ART heran: G_{\mu\nu}\space =\space k\space *\space T_{\mu\nu}
In den Tensoren G und T ist mit der jeweiligen Metrik, als Lösung der Gleichungen, der Aufbau der Raumzeit enthalten. Die Proportionalitätskonstante k kennt keine Metrik und sollte sich daher nicht um den Aufbau der Raumzeit kümmern müssen. Es sollten nur die Grenzbedingung enthalten sein. Diese ist nicht von der Metrik abhängig. Genauso ist es auch. Die normale Beschreibung von k baut sich wie folgt auf:
k\space =\space \cfrac{8\space *\space \pi\space *\space G}{c^4}
Wir setzen nun für G unsere neue Definition ein und erhalten:
k\space =\space \cfrac{8\space *\space \pi\space *\space d\space *\space c^4}{c^4}\space =\space 8\space *\space \pi\space *\space d
Wir erkennen sofort, dass G in den Feldgleichungen nicht benötigt wird. Man muss in der alten Beschreibung k explizit um die c^4 kürzen, damit man dort ein G verwenden darf. In der Metrik wir die Zeitdimension als Raumdimension behandelt. Die verschiedenen Dimensionen weisen ein abhängiges Verhalten als Raumdimensionen nur in der Metrik auf. G kennt dieses gegenseitige Verhalten nicht. Daher macht in dieser Beschreibung die c^4 in G auch Sinn. Ein c für jede Dimension getrennt.
Wenn wir G eliminieren, dann müssen alle Grenzen der Raumzeit in den Feldgleichung trotzdem vorkommen. Der Energie-Impuls Tensor T beschreibt die verschiedenen Formen der Energie. Da zur Beschreibung der Energie immer ein c notwendig ist, ist die niederdimensionale Grenze in T enthalten. Die höherdimensionale Grenze ist ein Widerstandswert der Raumzeit unabhängig von der Aufteilung der Raumzeitdichte in T. Daher dürfen wir dies aus T herausziehen und es darf ein k geben. In k darf dann nur noch die höherdimensionale Grenze enthalten sein. Damit ist k passend zu unserer Logik aufgebaut. Die Raumzeitdichte erzeugt gegen den Widerstand der Raumzeit die Raumzeitkrümmung.
Woher kommen die 8π? Wenn man die Feldgleichungen mathematisch aufbaut, ist es absolut klar woher die 8π kommen. Die mathematische Beschreibung gibt aber nie einen Grund an und zeigt immer nur wie es funktioniert. Wir wollen für alles einen Grund haben. Ich gebe hier einen sehr einfachen Hinweis:
8\space *\space \pi\space =\space 4\space *\space 2\pi
Könnt Ihr euch noch an das Beispiel mit dem Vergleich der elektrischen zur gravitativen Kraft zur Motivation von „alles ist ein Objekt“ erinnern. Da haben wir auf der einen Seite das Verhältnis der Kräfte und auf der anderen Seite das Verhältnis von Massen zum Quadrat.
\cfrac{F_{Elekt}\space *\space 2\space *\space \pi}{F_{Grav}\space *\space \alpha} =\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Ein Verhältnis von Masse kann nicht direkt ein Verhältnis von Kräften sein. Das sind zwei sehr unterschiedliche Blickwinkel auf das identische Objekt. Wir benötigen sowas wie eine Umrechnung von einem Blickwinkel auf den anderen Blickwinkel. Dies ist in dem Beispiel 2π und α. Bei α wird die Umrechnung je Wechselwirkung benötigt. Bei 2π je Raumdimension. Die Gravitation zwischen zwei Massepunkte wird als eine 1-dimensionale Verbindung gewertet. Wenn wir in der Feldgleichung die gesamte Raumzeit betrachten, brauchen wir dies 4-mal. Bei der Umrechnung von einem Blickwinkel Kraft der Raumzeit auf den Blickwinkel der Gravitation wird wohl immer je Raumdimension ein 2π benötigt. Die Dimensionale Konstante d ist ein Kehrwert der Kraft. Damit ist der Aufbau von k identisch zu unseren Kräftevergleich.
Das Warum dahinter konnte ich noch nicht zu 100% fixieren. Zurzeit 2026 läuft alles auf die folgende Erklärung hinaus. Der Auslöser der Raumzeitkrümmung muss in unserer Raumzeit liegen. Die Raumzeitdichte in einem Schwarzen Loch liegt aber hinter dem Ereignishorizont. Für die Energie ist der Ereignishorizont entscheidend. Dort kommt diese nicht mehr raus. Eine Geometrie in unserer Raumzeit folgt damit nicht einer geraden Linie zum Zentrum des Schwarzen Loches, sondern um dieses herum. Beim Kreisumfang kommt damit immer ein 2π mit rein. Damit haben wir eine erste unsichere Stelle in der DP gefunden. Zum Glück kommen nur wenige weitere dazu. Eine Stärke der DP.
Machen wir unser Trio an erklärbaren Naturkonstanten komplett. Es fehlt noch das h. Brauchen wir den das h überhaupt? Wir konnten aus c und d ein G erzeugen. Von G kennen wir den Wert. Dann haben wir drei Gleichungen mit drei unbekannten. Wir können damit die Planck-Werte bestimmen. Aus physikalischer Sicht erhalten wir aber aus G keine neue Information zur Raumzeit. Die Gravitationskontante ist nur eine Zusammensetzung aus bekannten Dingen. Wir brauchen eine zusätzliche Bedingung aus der Raumzeitgrenze.
Wie der Name schon sagt, ist h ein Wirkungsquantum. Schalten wir erstmal den Teil mit „Quant“ aus und konzentrieren uns auf die „Wirkung“. Wirkung bedeutet eine Veränderung. Von einem fixen Zustand auf einen anderen fixen Zustand. Die Wirkung beschreibt eine Zustandsveränderung. Der für uns erkennbare Zustand ist immer irgendeine Form von Energie, also Raumzeitdichte. Es geht um die Zustandsveränderung der Raumzeitdichte. Die höherdimensionale Grenze ergibt sich aus der Beschreibung der ART mit der Raumzeitkrümmung. Da steckt aber mit Sicherheit der Teil „Quant“ nicht drin. Eine Quantisierung der Raumzeitkrümmung ist noch niemanden gelungen. Also schauen wir uns die Kombination von Raumzeitdichte und niederdimensionaler Grenze an. Das Thema wird Teil 3 und die Beschreibung der gesamten QM ergeben. Hier betrachten wir nur den direkten Übergang in unsere Raumzeit. Die ART beschreibt das Verhalten in unserer Raumzeit mit den Grenzen, aber nicht außerhalb der Raumzeit.
Wir wollen die Beschreibung einer Wirkung von der niederdimensionalen Grenze in unsere Raumzeit hinein. Mit was starten wir? Genau, einer Länge. In der DP haben wir nur die Raumzeitdichte und damit muss sich alles auf eine Raumdimension abbilden. Wir brauchen immer eine Länge.
Schritt 1: h\space =\space l_P
Da wir aus dem niederdimensionalen eine Wirkung haben wollen, muss die Grenzbedingung erfüllt werden. Wir brauchen exakt einmal die Lichtgeschwindigkeit. Hier aber multiplikativ und nicht als Bruch. Wir wollen eine Wirkung erzeugen. Wir können unserer Raumzeit über diese Grenze nur einmalig erreichen. Die Zeitdimension ist bereits beim Fehlen einer einzigen Raumdimension auf null gesetzt. Das geht innerhalb einer Raumzeit nicht nochmal. Daher darf c keinen Exponenten haben.
Schritt 2: h\space =\space l_P\space *\space c
Dann fehlt uns noch mit was wir auf die Raumdimension wirken wollen. Viel Auswahlen haben wir in der DP nicht. Es muss eine Form von Raumzeitdichte sein. Nur direkt Energie, also die Raumzeitdichte in unserer Raumzeit kann es nicht sein. Da machen wir einen kleinen Vorgriff auf einen späteren Abschnitt. Über diese Grenze geht keine Zeit (Zeitdefinition auf null = Grenzbedingung), da die Zeitdimension immer an die jeweilige Raumzeitkonfiguration gebunden ist. Schauen wir uns die Definition der Energie nochmals an.
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
Der zweite Term kann es nicht sein. Ein Impuls ist die Erhöhung einer gegebenen Raumzeitdichte in 3D, in einer Richtung. Genau diesen Teil ist die Raumzeitdichte in unserer Raumzeit und kann damit nicht aus einer niederdimensionalen Raumzeit stammen. Mit einer Bewegung innerhalb unserer Raumzeit kommen wir bei der Beschreibung der Grenze nicht weit. Die Bewegung ist mit c aus Schritt 2 auch schon abgedeckt. Also der erste Term. Dort ist aber immer noch ein c vorhanden. Das c ist der Übertritt dieser Grenze und in Schritt 2 schon enthalten. Wir müssen die Energie ohne c benutzen. Damit ist eigentlich schon geklärt, was Masse ist. Eine Abbildung einer Raumzeitdichte von einer n dimensionalen Raumzeit in einer (n+1) dimensionalen Raumzeit. Daher ist es auch nicht verwunderlich, warum zur Beschreibung der Energie bei einer Masse immer die Raumzeitgrenzen mitspielen. Das machen wir aber exakter in einem späteren Abschnitt. Hier ist wichtig, wir können nur die Ruhemasse benutzen. Energie ohne den zeitlichen Bezug.
Schritt 3: h\space =\space l_P\space *\space m_P\space *\space c
Fertig! Die Wirkung aus einer niederdimensionalen Raumzeit in unsere Raumzeit darf nur so aussehen. Ok, aber was ist mit dem Teil „Quant“. Es könnte doch eine Abbildung auf einer beliebigen Länge, einer anderen Geschwindigkeit oder einer anderen Masse stattfinden. Warum die Planck-Werte unserer Raumzeit, wenn die Wirkung aus dem niederdimensionalen kommt? Insbesondere sagten wir vorher, dass im niederdimensionalen die Planck-Massen explizit andere sind als in unserer Raumzeit.
Die Grenzen kommen aus der ART. Diese beschreibt nur eine Raumzeit, unsere Raumzeit. Wenn wir irgendetwas durch eine Wechselwirkung Messen oder eine Information erhalten, dann passiert dies nur und ausschließlich in unserer Raumzeit. Energie ist die Raumzeitdichte unserer Raumzeit. Gerade sind wir noch auf dem Stand, dass wir nur Raumzeitdichte und Raumzeitkrümmung unserer Raumzeit erkennen können.
Dies bedeutet, dass eine beliebige Wirkung auf einer Raumzeitdichte eine Veränderung der Raumzeitdichte in unserer Raumzeit ist. Damit muss sich eine Wirkung an die Bedingungen unserer Raumzeit halten, egal aus welcher niederdimensionalen Raumzeitkonfiguration diese Wirkung kommt. Diese ist h zwischen den Grenzen c und d mit den bekannten Planck-Werten unserer Raumzeit. Das ist der Aufbau unserer Raumzeit. So bescheuert dieser Satz auch klingen mag: Die Quantisierung aller Wirkungen kommt nicht aus der QM, sondern aus der niederdimensionalen Grenze unserer kontinuierlichen Raumzeit.
Die Quantisierung durch h ergibt sich aus den charakteristischen Planck-Werten unserer Raumzeit durch die niederdimensionale Grenze
Damit dies Sache rund wird, gehen wir in den nächsten Abschnitt und schauen uns noch die Compton-Wellenlänge an.
Wieso packen wir hier noch die Compton-Wellenlänge mit rein. Diese zählt doch als Paradebeispiel der QM? Weil wir zu einer Wirkung noch einen Zustand benötigen. Leider wird dieser Umstand in den Lehrbuchbeschreibungen gut versteckt.
Die Bezeichnung ist oft der Compton-Effekt oder die Compton-Streuung. Es wird ein Photon auf ein Teilchen mit Ruhemasse geschossen. Das klingt doch sehr nach einem Prozess und nicht nach einem Zustand. Die passende Formel:
\Delta\lambda\space =\space \cfrac{h}{m_C\space *\space c}\space (1\space -\space cos\varphi)Die Formel beschreibt die Vergrößerung der Wellenlänge des Photons durch die Streuung. Was auffällt, der Zustand des Photons vor dem Prozess geht nicht in die Formel ein. Nur der Winkel ist entscheidend. Machen wir uns das Leben einfach und nehmen bei der Streuung einen Winkel von 90° an. Dann ist der Cosinus null. Die Formel vereinfacht sich und wir erhalten für eine Masse eine charakteristische Wellenlänge, die Compton-Wellenlänge:
\Delta\lambda\space =\space \cfrac{h}{m_C\space *\space c}Dies sieht doch schon wesentlich einfacher aus. Das tiefer gestellte große C bezeichnet die an der Streuung beteiligten Teilchen. In der Gleichung ist noch ein h enthalten. Das ist eine schlechte Darstellung. Die Formel beschreibt das Ergebnis nach dem Prozess und ist damit eine Beschreibung eines Zustandes.
Nehmen wir unsere neue Definition von h und setzen diese in die Formel ein:
\lambda_C\space =\space \cfrac{h}{m_C\space *\space c}\space =\space \cfrac{l_P\space *\space m_P\space *\space c}{m_C\space *\space c}\space =\space \cfrac{l_P\space *\space m_P}{m_C}\space \implies\space \lambda_C\space *\space m_C\space =\space l_P\space *\space m_P
Damit es etwas schöner aussieht, benennen wir \lambda_C in l_C um.
l_C\space *\space m_C\space =\space l_P\space *\space m_P
Dies ist ein gutes Ergebnis. Schauen wir uns an, was diese Formel alles aussagt:
Wer sich gewundert hat, dass wir aus der ART heraus eine Quantisierung erzeugen können, muss jetzt mal auf die Zähen beißen. Wir legen noch eine Schippe drauf. Tief durchatmen und los.
Der Zustand einer einzelnen Raumzeitdichte ist mit l_P\space *\space m_P fix festgelegt. Die Veränderung mit einem h ist nur eine andere Aufteilung auf der Seite mit der inneren Struktur l_C\space *\space m_C. Das ist der Grund, warum h der QM zugeschlagen wird. Die Definition kommt aber aus der Grenze unserer Raumzeit.
Das war jetzt starker Tobak, es fehlen jedoch noch zwei wichtige Eigenschaften aus der Grenze der Raumzeit heraus. Wir kümmern uns erstmal um diese Themen und kehren dann nochmals zur Ruhemasse zurück.
In der bisherigen Logik ist es nicht 100% klar, warum wir Schnittstellenobjekte in unserer Raumzeit erkennen können. Es stellt sich folgende Frage. Welche Eigenschaften können wir über eine dimensionale Grenze hinweg erkennen? Wir sind uns sicher, dass wir was erkennen können müssen. In unserer Raumzeit gibt es Photonen, als Objekte für die niederdimensionale Grenze und Schwarze Löcher, als Objekte für die höherdimensionale Grenze.
Wir werden sehen, dass wir nur sehr wenige Eigenschaften über die dimensionale Grenze hinweg erhalten können. Das wird gegen die normale Intuition laufen. Dabei gibt es zwei große Bereiche. Die Zeit als eigenen Bereich behandeln wir im nächsten Abschnitt 3.9. Hier kümmern wir uns um die Geometrie von Objekten und damit um die Geometrie der Raumzeit.
Das ein Schwarzes Loch irgendeine Form von Übergang sein soll ist ein alter Hut. Dazu gibt es jede Menge verschiedene Ideen. Eine davon ist zum Beispiel das Stichwort: Wurmloch. Wenn man es mal nicht so streng sieht, dann sieht der höherdimensionale Übergang auch nur wie ein Wurmloch aus. In der DP in eine höherdimensionale Raumzeit. Mit den Zutaten Schwarzes Loch und Übergang kommt man sehr leicht auf diese Idee. Leider passt das Wurmloch nicht. Um es auf den Punkt zu bringe, die Idee eines Wurmloches ist komplett falsch.
Das Problem sind Grafiken dieser Art
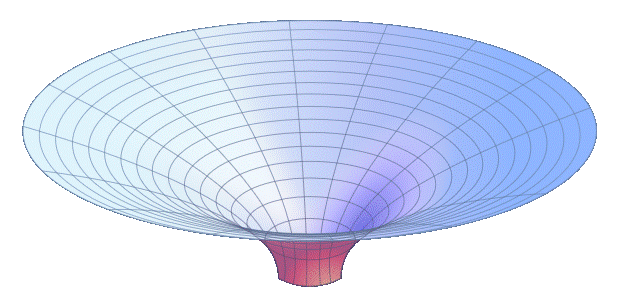
Eine Raumzeitkrümmung aus unserer Raumzeit 3D wird auf eine Abbildung in einer 1D Raumzeit zurückgeführt (Eine Raumkomponente radial und eine Zeitkomponente diagonal). Mathematisch ist da alles mit einer Einschränkung sauber. Die ART braucht für die Raumzeitkrümmung keinen höherdimensionalen umgebenden Raum. Das Bild zeigt die 1D Raumzeitkrümmung explizit mit einer extrinsischen Ausprägung in 3D. Das ist laut ART falsch. Man kann es aber nicht anders darstellen. So ein Bild der Raumzeit als Trichter wird als Wurmloch bezeichnet. Entscheidend ist der „Boden“ des Trichters. Wohin geht das „Loch“. Genau hier liegt das Problem. Es gibt kein Loch.
Das Bild mit dem Trichter führt einen auf den Gedanken, dass ein Wurmloch durch die Raumzeitkrümmung erzeugt wird. Das ist auch die allgemeine Lehrbuchmeinung in der Physik. Hier aus der DP heraus ein klares, Nein! Die Raumzeitkrümmung hat nichts, aber auch gar nichts mit dem Übergang zu tun. Das Trichterbild führt uns auf den falschen Pfad. Die Bedingung für den Übergang ist: d\space =\space \frac{l_P}{E_P}.Da steht was von Länge und Raumzeitdichte. Da kommt keine Raumzeitkrümmung vor. Die Raumzeitkrümmung ist der Ausgleich der Raumzeit zu einer Raumzeitdichte. Der Übergang ist die Raumzeitdichte und nicht die Raumzeitkrümmung. Ok, der Übergang liegt auf dem Boden des Trichters und die Raumzeitkrümmung führt dort hin. Die Raumzeitkrümmung ist aber nicht der Übergang. Es gibt keine Singularität der Raumzeitkrümmung. Der Boden muss in dieser Darstellung einfach eine flache Scheibe sein. Die Raumzeitkrümmung geht nur bis zur Raumzeitdichte. Damit ist der Boden flach. Genau dieser flache Boden ohne Raumzeitkrümmung muss mit einer höheren Raumzeit verbunden sein.
Die Raumzeitdichte und nicht die Raumzeitkrümmung ist der Grund für den höherdimensionalen Übergang
Gegenprobe: Wenn der Übergang in der Raumzeitkrümmung liegt, dann müsste es für die Raumzeitkrümmung einen maximalen Wert oder eine Singularität geben. Bei der Singularität haben wir einen unendlichen Wert, das kann kein Übergang sein, das ist nicht definiert. Haben wir einen maximalen Wert, dann müsste das Wachstum eines Schwarzen Loches begrenzt sein. Die Raumzeitkrümmung erreicht dann nur noch diesem Wert. Es könnte nicht noch mehr Materie in das Schwarze Loch fallen. Eine Wachstumsgrenze für ein Schwarzes Loch ist nicht bekannt.
Was können wir an einer Raumzeitdichte, welche auch in 4D liegt, erkennen? Das können nur noch die über den Übergang verbundenen Eigenschaften aus unserer Raumzeit sein. Bei der Raumzeitdichte ist dies nicht viel. Wir erkennen nur die Eigenschaften der Energie. Holen wir mal wieder die Formel für die Energie:
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
Der erste Term ist dann die Ruhemasse des Schwarzen Loches. Der zweite Term ist die Bewegung des Schwarzen Loches in unserer Raumzeit. Da ist der Impuls und der Drehimpuls. Ende der Fahnenstange, mehr haben wir nicht.
Moment mal! Wir kennen uns doch in dem Thema aus. Ein Schwarzes Loch hat zur Masse und Eigenbewegung noch mindestens die Eigenschaft elektrische Ladung. Die Ladungen dürfen nicht einfach verschwinden. Das führt uns direkt zum Informationsparadoxon eine Schwarzen Loches.
Die erste Begrenzung über den Inhalt des Schwarzen Loches kommt aus der Raumzeitkrümmung. Wir stimmen mit der QM überein, dass alle Wechselwirkungen des Standardmodells ohne Gravitation nur über Austauschteilchen übermittelt werden können. Das schnellste davon ist, das Photon. Ein Schwarzes Loch zeichnet sich gerade dadurch aus, dass auch ein Photon den Ereignishorizont nicht verlassen kann. Damit kann keine einzige Eigenschaft aus der QM außerhalb des Ereignishorizontes bekannt sein.
Es ist in der QM ein mathematisches Theorem, dass eine Information nicht einfach verschwinden kann. Da wir die Mathematik zur QM nicht verändern, sondern bestätigen, müssen wir uns an dieses Theorem halten. Das wir Menschen außerhalb des Schwarzen Loches an diese Information nicht mehr herankommen ist aber nicht das Paradoxon, sondern nur unsere eigene Arroganz. Dies ist nicht wichtig.
Das Problem liegt z.B. in der Hawking-Strahlung. Der exakte Mechanismus ist hier nicht relevant. Wichtig ist, dass ein Schwarzes Loch seine Energie durch Teilchen abgeben kann, welche gar nicht hinter dem Ereignishorizont waren. Die Teilchen vom Rand des Ereignishorizontes tragen damit keine Information aus dem Schwarzen Loch heraus. Das Schwarze Loch verliert trotzdem Masse und löst sich sehr, sehr langsam auf. Wo ist die Information der Teilchen im Schwarzen Loch hin?
Die Information ist tatsächlich, auf dem „Boden“ des Trichters, nicht mehr vorhanden. Wir verletzten das Informationstheorem trotzdem nicht. Den Grund könnt ihr euch vermutlich schon denken. Der dimensionale Übergang. Der niederdimensionale Übergang zwischen 3D und 2D erzeugt die gesamte QM. Nur im Zentrum eines Schwarzen Loches sind wir beim Übergang von 3D auf 4D.
Die Bedingung für ein Schwarzes Loch ist: d\space =\space \cfrac{l_P}{E_P}
Die Bedingung für eine Abbildung über die niederdimensionale Grenze ist:
Wirkung: h\space =\space l_P\space *\space m_P\space *\space c
Zustand: l_C\space *\space m_C\space =\space l_P\space *\space m_P
Die Bedingung in d ist explizit so, dass wir entweder eine Länge kleiner l_P haben oder Energie mit einer Masse größer m_P. Dann können wir über die niederdimensionale Schnittstelle weder eine Wirkung noch einen Zustand in unserer Raumzeit abbilden. Das passt sehr gut, da die Bedingung für ein Schwarzes Loch ist, dass die Raumzeitdichte nicht mehr in unserer Raumzeit abgebildet werden kann. Dann können wir dafür auch keine 2D Abbildung mehr erhalten.
Das macht absolut Sinn. Die QM bildet sich über die Schnittstelle 2D zu 3D. Im Schwarzen Loch sind wir aber aus der Raumzeit raus oder besser, genau auf der Grenze zu 4D. Da gibt es keine 2D-Abbildung mehr. Mit der Bildung eines Schwarzen Loches, verliert die 3D Raumzeitdichte ihre 2D Abbildung für die QM. Die QM ist dort nicht mehr zuständig und kann keine Aussage zum höherdimensionalen Übergang machen. Es gibt keine Informationsparadoxon aus der QM heraus in einem Schwarzen Loch. Die QM verliert im Zentrum eines Schwarzen Loches ihre Gültigkeit. Es gibt tatsächlich keine niederdimensionale „innere“ Struktur der Raumzeitdichte in einem Schwarzen Loch. Damit keine Informationen. Die QM verliert keine Information für sich selbst, diese ist dort einfach nicht mehr aussagefähig. Es ist sogar umgekehrt richtig. Wenn die Hawking-Strahlung aus einem Schwarzen Loch dessen Information herausbringen würde, dann hätten wir ein Problem.
Eventuell könnt ihr ab hier erahnen, wie ich mich fühle, wenn immer und immer wieder die große Versprechung kommt, dass nur die QM mit einer irgendwie gearteten Quantengravitation das Rätsel der Singularität in einem Schwarzen Loch lösen kann, lol.
Die exakte Beschreibung der Schnittstelle ist der gesamte Teil 3 QM. Hier gehen wir nur auf einen Punkt ein. Wenn alles eine Verformung der Raumzeit durch Dichte und Krümmung ist, warum können wir diese Geometrie nicht direkt aus dem niederdimensionalen erkennen. Wir sagen nicht, dass ein Elementarteilchen eine Raumzeitkrümmung nach oben oder unten hat. Es kommen neue Bezeichnungen wie Spin und Ladung dazu. Dies deutet darauf hin, dass man eine Raumzeitgeometrie über einen dimensionalen Übergang nicht so einfach erkennen kann.
Das Ganze ist sogar noch viel wilder. Man kann, in einem ersten Ansatz, über so eine Grenze überhaupt keine Geometrie erkennen. Die Stelle wäre fast das Ende der DP gewesen. Es war klar, dass dieser Übergang eine der wichtigsten Eigenschaften der DP sein wird. Ich konnte aber, eine sehr lange Zeit, keine geometrische Abbildung über die Grenze hinweg finden. Im Nachgang war die Lösung so einfach und offensichtlich, dass ich mich dafür wirklich geschämt habe. Wenn mal die Lösung da ist, ist alles sehr einfach. Man muss aber erstmal darauf kommen. Die Lösung ist die Schnittstelle selbst. Ab diesem Punkt haben sich dann fast alle weiteren Probleme wie von selbst gelöst. Es bedurfte dann nur noch etwas Zeit und Hirnschmalz.
Das eigentliche Problem ist nicht ein niederdimensionaler Übergang, sondern grundsätzlich der Übergang mit einer unterschiedlichen Anzahl von Raumdimensionen. Das Problem ist in jeder n-dimensionalen Raumzeit vorhanden.
Wir starten einfach in unserer Raumzeit und stellen uns ein Volumen vor. Länge * Breite * Höhe. Das Volumen hat in unserer Raumzeit eine Ausdehnung und eine Oberfläche. Das ist noch alles klar. Jetzt nehmen wir eine zweidimensionale Fläche mit Länge * Breite und Höhe = 0. Eine Raumdimension muss null sein. Das ist die Definition von niederdimensional. Dann sind das Volumen und die Oberfläche per Definition auch null.
Aber wir können doch für die Fläche Länge, Breite und Flächeninhalt angeben. Das sind gute Abmessungen. Ja schon, aber das ist wieder eine mathematische Abstraktion, ähnlich der Diskussion mit dem Punkt, dieses Mal auf 2D. In 3D können wir den Anfang oder das Ende von Länge oder Breite nicht erkennen. Die Höhe ist null. Für uns als 3D-Wesen ist da Nichts. Eine 2D-Fläche ist mathematisch abstrakt beschreibbar, aber real in einer 3D-Raumzeit nicht erkennbar. Das wir auch nicht besser, wenn wir aus der Fläche eine Sphäre machen (ein geschlossenes Objekt). Denn die Höhe oder Dicke der Fläche, welche die Sphäre begrenzt, ist per Definition null. Da ist nichts.
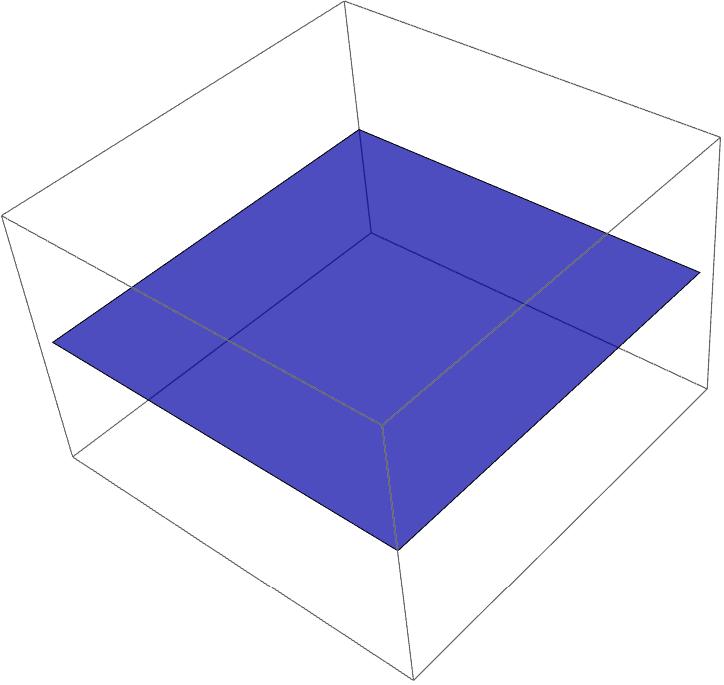
Wie wollen wir die Fläche in 3D als Objekt erkennen können, wenn wir auf Grund der fehlenden Höhe einen Beginn oder ein Ende der Länge oder Breite nicht feststellen können?
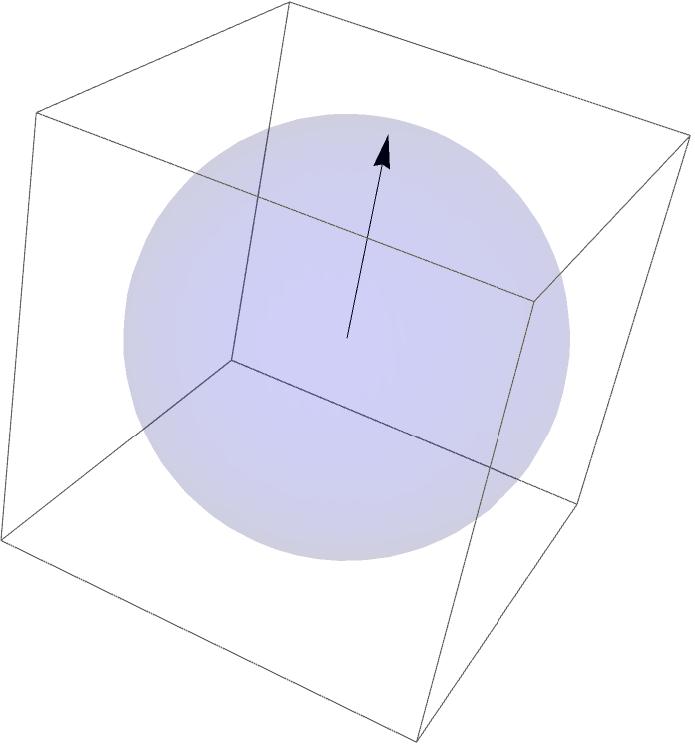
Das sieht doch erstmal nach einem 3D Objekt aus. Nur dazu müssten wir die Hülle, mit dem Radius feststellen können. Aber genau die Höhe der Hülle ist per Definition auf null festgesetzt. Da gibt es nichts, wo wir einen Radius festlegen können. Damit können wir dieses vermeidliche 3D Objekt in unserer Raumzeit nicht feststellen.
Wir können eine Fläche wie ein Blatt Papier beliebig „zusammenknüllen“. Das Blatt Papier hat ein Volumen. Daher erkennen wir jede veränderte Form davon. Eine Fläche hat kein Volumen und keine Oberfläche. Daher können wir diese Fläche in keiner Form erkennen.
Das Ganze muss sich jeder mal separat in einem ruhigen Stunden selbst überlegen. Ihr kommt auf folgendes Ergebnis:
Über die dimensionale Grenze kann keine geometrische Größe weitergeben werden
Länge, Volumen, Oberfläche oder auch nur eine Entfernung, sind Angaben, welche immer nur in der eigenen n dimensionalen Raumzeit eine sinnvolle geometrische Angabe entsprechen. Es ist vollkommen egal, welche Form die nieder- oder auch höherdimensionale Geometrie hat. In der eigenen Raumzeit ist diese Geometrie nicht erkennbar. Das ist verdammt wenig. Wir werden in Teil 3 sehen, dass genau dieses Verhalten und die fehlende Zeit aus Abschnitt 3.9 die Beschreibung der QM so „seltsam“ werden lassen.
Wir müssten schon irgendetwas erkennen können, sonst ist unser Ansatz falsch. Es ist aber gar nicht notwendig, geometrische Form erkennen zu können. Wir müssen eine Raumzeitdichte erkennen können. Darauf baut alles auf.
In der Lehrbuchbeschreibung der ART liegt die Raumzeitkrümmung und damit auch die Raumzeitdichte immer intrinsisch in der Raumzeit. Holen wir unser Trichterbild, Abbildung 3-1. Wichtig, das Bild ist aus rein mathematischer Sicht eine 100% richtige Darstellung. Nur für die Sichtweise der ART darf es keine extrinsische Krümmung geben.

Das bedeutet, die Raumzeitkrümmung muss in der Ebene liegen. Bei dem Trichter wird die Raumzeitkrümmung aber explizit aus der Ebene heraus nach unten gezeichnet. Damit ist dies eine extrinsische Darstellung und für die ART eigentlich falsch. Wirklich? Warum will man in der ART keine extrinsische Darstellung haben? Genau hier liegt die Lösung.
Unsere 3D Raumzeit müsste in eine höhere Raumzeit eingebettet sein. Da man mit so wenig zusätzlichen Annahmen wie möglich auskommen will, lässt man dies weg und macht die Abbildungen intrinsisch. Das ist mathematisch kein Problem. Die Beschreibung der ART könnte aber genauso gut extrinsisch erfolgen. Das ist die Anwendung von Ockhams Rasiermesser.
Zum Glück sind wir in der Beschreibung der DP. Durch die Raumzeitgrenzen ergibt sich zwingend, dass unsere Raumzeit in mindestens eine höherdimensionale Raumzeit eigebettet ist, da wir Schwarze Löcher haben. Die Raumzeitgrenzen existieren. Daraus folgt für uns, dass wir ohne Einschränkung eine extrinsische Beschreibung benutzen dürfen. Wir werden in Teil 3 erkennen, dass wir bis auf eine Ausnahme, die Ruhemasse, sogar nur extrinsische Eigenschaften erkennen können.
Hier ein falsches Bild von einer 2D Fläche in einem 3D Volumen. Da kann in der 2D Fläche so viel 2D-Geomerie vorhanden sein wie will. Wir können nichts erkennen. Die Fläche ist nur eine Abstraktion.


Wenn wir die 2D-Fläche aber extrinsische zu einer Welle verformen, dann enthält das 3D Volumen mehr 2D-Raumzeit. Das ist eine Erhöhung der Raumzeitdichte im 3D-Volumen. Da ist mehr niederdimensionale Raumzeit enthalten. Das bedeutet, wenn wir uns von der Vorgabe keine extrinsische Verformung zu benutze lösen, dann haben wir eine Möglichkeit für eine erkennbare Raumzeitdichte gefunden.
Die dimensionale Schnittstelle, welche keine geometrischen Eigenschaften übergibt, bedingt durch die Einbettung aber auch, dass wir eine extrinsische Ausprägung benutzen können. Diese Ausprägung können wir in 3D erkennen. Eine Wellendarstellung kann in 2D selbst nicht erkannt werden. Es muss immer über die Raumzeitdichte gehen. Das bedeutet, dass ein Photon (eine Darstellung auf nur 2 Raumdimensionen) zwingend eine Wellendarstellung sein muss. Es ist aber eine Wellendarstellung einer einzigen Raumzeitdichte. Teilchen und Welle gleichzeitig. Das ist kein Fehler oder Paradoxon, dies ist in diesem einfachen Bild tatsächlich richtig. Damit können wir auch erklären, warum für ein Photon die Wellenlänge und nicht die Amplitude die Energie angibt. Wenn wir die Amplitude erhöhen, dann müssten wir auch das betroffene Volumen erhöhen. Die Amplitude wird größer und die Höhe des Volumens wächst identisch an. Damit erhalten wir keine größere Raumzeitdichte in einem Volumen. Nur wenn wir die Wellenberge zusammenschieben, erhalten wir mehr 2D Fläche im gleichen Volumen. Vollkommen unabhängig von der Amplitude.
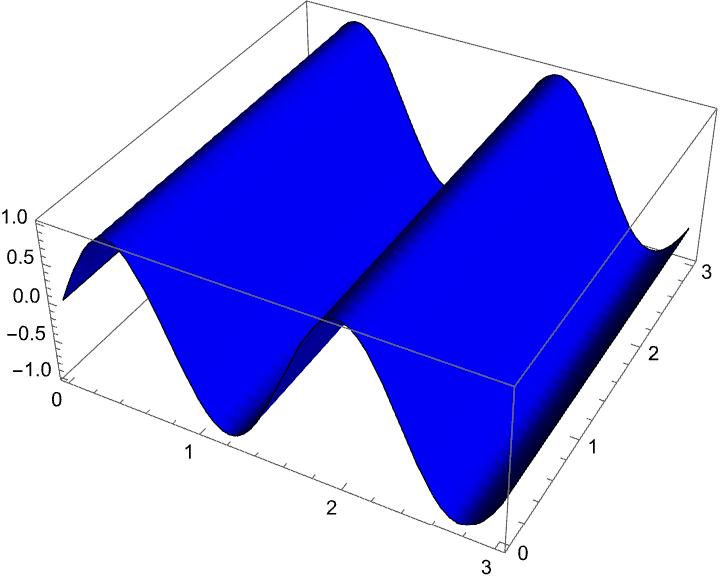
Das ist ein sehr einfaches Bild (bei exakter Beschreibung sogar ein falsches Bild) von einem Photon, das werden wir aber in Teil 3 genauer besprechen. Die Wellen läuft hier in die falsche Richtung! Es fehlt die Raumdimension in Richtung der Amplitude. Dann müsste sich das Photon in dieser Richtung bewegen. Für eine Darstellung einer Analogie ist dies aber passend. Wir haben hier erstmal einen möglichen Übergang für die Abbildung von Raumzeitdichte in 3D gefunden.
Wellenabbildung klingt schon mal, als ob es für die QM in die richtige Richtung geht. Für die QM müssen wir den gesamten Teilchen-Zoo des Standardmodells in niederdimensionalen Raumzeitkonfigurationen abbilden. Da ist die Möglichkeit mit der extrinsischen Abbildung schon mal ein Anfang. Das reicht für die benötigte Vielfalt aber niemals aus. Schön zu wissen, dass da noch was fehlt. Nur was ist es denn? Die Lösung haben wir uns jetzt schon 2-mal angeschaut und darüber diskutiert.
Trommelwirbel, die Lösung ist: Der Trichter. Das Bild lasse ich hier weg, sonst wäre es keine Überraschung geworden. Über den Trichter in Verbindung mit den Raumzeitgrenzen, sind wir auf die Idee gekommen, dass wir eine extrinsische Abbildung wie den Trichter benutzen dürfen. Frage: Welches Objekt soll der Trichter den abbilden? Genau, eine Schwarzes Loch. Was ist ein Schwarzes Loch? Richtig, der höherdimensionale Übergang. Wir brauchen im niederdimensionalen eine Abbildung eines Schwarzen Loches. Dann haben wir einen höherdimensionalen Übergang von 2D auf 3D und sind genau da, wo wir hinwollen, in unserer Raumzeit. Das steht hier in dem Absatz so einfach da. Glaubt mir, diese einfache Idee war eine schwere Geburt.
Dieses Schwarze Loch ist dann auch gleich der Grund für Teilchen mit Ruhemasse. Witzig ist, dass es in etlichen Lehrbüchern eine kleine Rechnung zu einem Schwarzen Loch gibt. Berechnen Sie bitte, warum ein Elektron kein Schwarzes Loch sein kann. Die Berechnung ist einfach und hat als Ergebnis einen Schwarzschildradius von ca. 1,353\space *\space 10^{-57} für das Elektron. Dies ist kleiner als die Planck-Länge. Damit kann ein Elektron kein Schwarzes Loch sein. Wir werden später sehen, dass diese Aussage für unsere Raumzeit absolut richtig ist. Es gibt eine minimale Grenze für den Schwarzschildradius. Der ist beim Elektron um viele Größenordnungen unterschritten. Das Elektron ist aber das perfekte Schwarze Loch in einer 2D Raumzeit. Mit einem wesentlich kleineren Dimensionalen Konstante als in dieser Raumzeit. Jede Raumzeit hat ihre eigenen Planck-Werte. Die Planck-Masse einer einfachen 2D Raumzeit kennen wir jetzt schon, die Ruhemasse des Elektrons.
Dem Mysterium der Zeit gebührt mit Sicherheit mehr als nur ein Abschnitt in diesem Kapitel. Wir dürfen uns sicher sein, dass wir dies nicht vollständig lösen werden. Wir benötigen für die DP aber eine passende logische Beschreibung der Zeit. Dies wird hier besprochen, da in der DP die Zeit nur im Zusammenhang mit den Raumzeitgrenze verständlich ist.
Zeit ist immer mit einer Veränderung verbunden. Ohne eine Veränderung könnte auch keine Zeit erkannt werden und umgekehrt. In der DP ist alles, was wir erkennen können mit mindestens einer Raumdimension verbunden. Um eine Dichte abbilden zu können benötigen wird mindestens eine Raumdimension. Eine Veränderung einer Abbildung ist damit immer die Veränderung von Raumdimension und der Zeit. Zeit und Raum sind damit nicht unabhängig.
Wir sind bereits mit einem Ansatz aus der ART gestartet. Daher ist es klar, dass wir mit einer Raumzeit als ein untrennbares Objekt arbeiten müssen. Es macht aber trotzdem Sinn, sich diese Einheit als Folgerung einer Dichte auf die Raumdimension herzuleiten. Da Raum und Zeit nicht unabhängig sind, bleiben wir bei der Raumzeit und Raumzeitdichte.
Es bleibt aber die Frage offen, warum den die Zeit nicht einfach gleichbleibend vergeht, wenn sich die Raumdichte verändert. Das liegt daran, dass die Veränderung der Raumdichte eine Veränderung der Raumdefinition ist. Die Geschwindigkeit ist Länge durch Zeit. Die Zeit bleibt gleich, die Länge wird bei Beschleunigung aber „kürzer“. Das Objekt würde bei Beschleunigung langsamer werden. Das entspricht wohl nicht der Beobachtung. Die Rechnung der ART funktionieren nur, weil man aus der Zeitdimension eine Raumdimension gemacht hat. Nochmal: Die Zeitdimension ist in der ART wie auch in der SRT eine Raumdimension mit unterschiedlichen Vorzeichen. Bei der Raumdimension verändert sich die Definition der Geometrie. Damit muss sich auch die Zeitdimension als die Definition der Zeit verändern. Raum- und Zeitdimension verändern die Definition was eine Längeneinheit oder eine Zeiteinheit ist. Da wird nichts gequetscht oder gezogen.
Die Zeit ist damit an die Raumzeitkonfiguration gebunden. Verändert sich diese Konfiguration, zum Beispiel eine Raumdimension weniger, dann ist dies nicht mehr die identische Raumzeit. Das Objekt Raumzeit wird verlassen. Dann muss auch die Zeit gegen null laufen. Daher muss jede Raumzeitkonfiguration seine eigene Zeitdimension haben.
Daraus können wir für uns folgende Dinge ableiten:
Die Raumzeitgrenzen sind aus Sicht der Zeit erreicht, wenn wir keine Wirkung an einem Zustand mehr erreichen können, keine Veränderung mehr. Dann können wir keine Zeit mehr feststellen. Schauen wir uns nochmal die kleinen Formeln zu Wirkung und Zustand in unserer Raumzeit an:
Wirkung: h\space =\space l_P\space *\space m_P\space *\space c
Zustand: l_C\space *\space m_C\space =\space l_P\space *\space m_P
Nehmen wir jeweils nur die rechte Seite und setzen die Wirkung zu Zustand ins Verhältnis:
\cfrac{Zustand}{Wirkung}\space =\space \cfrac{l_P\space *\space m_P}{l_P\space *\space m_P\space *\space c}\space \cfrac{1}{c}
Das ist der „Widerstandswert“ der Raumzeit gegen eine Veränderung. Der ist bei c überbrückt und es kann keine Veränderung mehr geben. Die Wirkung aus dem niederdimensionalen muss die Zustandsabbildung aus dem niederdimensionalen noch verändern können. Das ist die niederdimensionale Grenze.
Wir können aus diesen Überlegungen die Zeit mit dem Abstandsmaß zu den Grenzen der Raumzeit gleichsetzen.
Die Zeit ist ein Abstandsmaß zur Raumzeitgrenze
Damit gibt es in der DP keinen Fluss der Zeit oder einen Zeitpfeil. Die bessere Sichtweise ist, dass das Erleben der Zeit die ständige Abstandsmessung zur Raumzeitgrenze ist. Daher erleben wir keine Vergangenheit. Es kommt immer die nächste Messung zur Grenze. Der „Messwert (Die Definition der Zeiteinheit)“ kann sich aus der Vergangenheit wiederholen. Es ist aber eine andere Messung. Der Zeitfluss ist die Reihe der Abstandsmessungen.
Zum Abschluss noch eine oft gestellte Frage: Warum gibt es nur eine Zeitdimension? Diese Frage lässt sich mit unserer neuen Sichtweise leicht erklären. Das Objekt Raumzeit kann genau einmal verlassen werden. Dann ist man raus. Wir können die Raumzeit nicht nochmal verlassen, wenn wir schon draußen sind. Daher kann es nur eine Zeitdimension geben. Der Zeitverlauf ist die Abstandsmessung zur Raumzeitgrenze. Es ist nur eine Zeitdimension je Raumzeit möglich.
Die Idee, dass die Zeit eine Abstandsmessung ist, hat noch einen weiteren Grund: Das Relativitätsprinzip. Damit lässt sich eine lokal gleichbleibende Zeit sehr gut erklären. Das wird im nächsten Kapitel durchgearbeitet.
Es gibt separate Wert je Elementarteilchen für die Ruhemasse und nicht wie bei h einen Wert für alle. Klar, h kommt aus der Schnittstelle und gilt einfach für alles aus dem Niederdimensionalen. Die Ruhemasse ist eine niederdimensionale Raumzeitdichte. Die Ruhemassen sind für sich auch ein Quantum. Je Teilchen/Raumzeitkonfiguration gibt es nur mit einem bestimmten Wert und dann ein Vielfaches davon.
Jede Raumzeitkonfiguration hat ihre eigene Planck-Werte und in 2D ist jede Abbildung, die wir in 3D mit Ruhemasse wahrnehmen eine Abbildung mit mindestens einem Schwarzen Loch. Die Ruhemasse für ein Elektron ist in 2D die dortige Planck-Masse für die Dimensionale Konstante. Die Ruhemasse ist die Energie oder Raumzeitdichte ohne den zeitlichen Anteil.
Schauen wir uns dies mit etwas Mathematik an. Für die Ruhemasse können wir wieder die berühmteste Formel der Welt benutzen: E\space =\space mc^2. Wenn wir in unserer Raumzeit aus der Ruhemasse eine Energie machen wollen, dann müssen wir immer ein c^2 einfügen. Warum eigentlich? Ich hoffe, dass inzwischen keiner mit den Gedanken kommen will mit: „na, die Formel gibt dies so vor“. Ja das tut die Formel und die Maßeinheiten müssen übereinstimmen. Wir müssen aus der Logik der DP heraus erklären, warum wir ein c^2 benutzen. Das ergibt sich wie immer aus der Schnittstelle. Die Überlagerung von 3D zu 2D ist nur im Raum. Damit haben wir im ersten Schritt nur zwei Raumdimensionen belegt. Da in 2D die Dimensionale Konstante überschritten wurde, werden für die Abbildung mehr Raumdimensionen benötigt. Eine Energie und damit Raumzeitdichte in unserer Raumzeit muss aber alle 3 Raumdimensionen und die Zeitdimension belegen. Der Übergang ist immer eine Raumdimension und eine Zeitdimension. Wobei die Zeitdimension eine „verkappte“ Raumdimension ist. Da wir dafür den „Übergang“ schaffen müssen, brauchen wir je Raumdimension ein c und landen bei c^2. Also müssen wir immer ein c^2 multiplizieren. Die Logik stimmt für beliebig dimensionale Raumzeiten, da wir immer nur den Übergang in eine Raumdimension höher n+1 oder niedriger n-1 schaffen. Wir können schon bei einer Raumdimension mehr oder weniger fast keine Eigenschaften mehr erkennen. Bei zwei Raumdimensionen mehr erkennen wir gar nichts mehr. Bei zwei Raumdimensionen weniger geht es nur über einen Umweg, den wir bei den Neutrinos nutzen werden. Daher ist E\space =\space mc^2 für alle beliebigen Raumzeiten universell gültig.
Noch ein Wort zu den Maßeinheiten von Energie, Kraft und einer Wirkung. Als erstes schreiben wir uns für die drei Werte die Maßeinheiten auf:
Allein wie wir die Maßeinheiten hinschreibe verweist auf eine bestimmte Richtung, wie dies zu lesen ist. Die Energie haben wir gerade geklärt und daher sehen die Maßeinheiten dort so aus. Wir hätten die Energie auch wie folgt schreiben können: [kg\space *\space m\space *\space\cfrac{m}{s^2}\space]. Dann sieht es so aus, dass die Energie eine Beschleunigung beinhaltet und damit eine immerwährende Veränderungsrate. Ist für eine Größe, die sich selbst nicht verändern kann, etwas seltsam. Mit unserer Logik ist die Lesart der Maßeinheiten festgelegt. Bei der Kraft wird explizit etwas verändert. Bei der Angabe der Kraft wird die Veränderung als Beschleunigung, also als eine Veränderungsrate angegeben. Bei der Wirkung kommen die Maßeinheiten zustande, da es eigentlich eine Energie * Zeit ist und sich daher die Zeit im Nenner einmal weg kürzt. Also eine kontinuierliche Portion an Energie über eine Zeit. Da darf es keine Beschleunigung geben. Es ist die Veränderung von einem Zustand in einen neuen Zustand. Da sich die Ruhemasse nicht verändern kann, ist es hier immer eine Veränderung des Impulses. In der Wirkung steckt daher auch ein Impuls mit: [kg\space *\space \cfrac{m}{s}\space] mit drin. Wie sich dieser Impuls auf eine Länge verteilt, ist dann die Wirkung. Verteilt sich der Impuls auf eine kleine Länge, dann ist es eine große Wirkung und umgekehrt. Wir wollen hier alles erklären. Das normale Vorgehen in der Physik mit, wir setzen G (bei und d), h und c auf 1 und schieben später im Ergebnis alles nach, damit die Maßeinheiten stimmen, können wir uns nicht leisten. Das geht nur beim Berechnen ohne Nachdenken, aber nicht beim Erklären.
Können wir die Planck-Werte in einer Raumzeitkonfiguration berechnen. Ja und Nein. Ohne eine weitere Annahme für die Berechnung kommen wir auf keinen grünen Zweig. Die Planck-Werte je Raumzeitkonfiguration sind einfach gegeben. Ich habe 2026 noch keine Möglichkeit gefunden, diese berechnen zu können. Wir können aber mit einem kleinen Vorgriff auf ein späteres Thema eine Berechnung ausführen. Der Vorgriff ist, dass wir die elektromagnetische Kraft als niederdimensionale Gravitation ansehen werden. Zusätzlich ist hier nochmals darauf hingewiesen, dass wir eine Ruhemasse aus 2D nur in unserer 3D Raumzeit mit den uns bekannten Werten feststellen können. In 2D selbst sieht dies nochmals anders aus.
Nehmen wir etwas, dass wir kennen: Den Kräftevergleich der Gravitation und dem elektrischen Feld. Ich schreibe schon mal die Lösung hin.
\cfrac{F_{Elek}}{F_{Grav}}\space =\space \cfrac{\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space r^2}}{\cfrac{G\space *\space m_1\space *\space m_2}{r^2}}\space =\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space G\space *\space m_e^2}\space =\space 4\space *\space 10^{42}\space = \bigg(\cfrac{1}{2\space *\space \pi}\bigg)\space *\space \alpha\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Bei den Termen auf der rechten Seite, kommt keine Gravitation oder ein elektrisches Feld vor. Die Werte sind trotzdem identisch. Wie soll das denn gehen? Nach der Annahme, dass Gravitation als Kraft und das elektrische Feld als Kraft, sich nur in der Anzahl der Dimensionen unterscheiden, müsste dieser Vergleich nur von dem Unterschied in den Planck-Werten und vom niederdimensionalen Übergang abhängen. Genau dies sehen wir hier.
Die mathematische Erklärung ist sehr einfach. Wir nehmen der Term in der Mitte:
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space G\space *\space m_e^2}
Schritt 1: Wir schreiben unsere Definition von G in die Formel.
\cfrac{e^2\space *\space m_P}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_e^2}
Schritt 2: Wir erweitern den Bruch mit einer Planck-Masse m_P.
\cfrac{e^2\space *\space m_P^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_P\space *\space m_e^2}\space =\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_P}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Schritt 3: Wir ziehen das c^2 auseinander und schauen uns den Nenner genauer an.
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c\space *\space c\space *\space m_P}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Schritt 4: Im Nenner ist nun ein h\space =\space l_P\space *\space m_p\space *\space c versteckt.
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space h\space *\space c}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Schritt 5: Dann ist der erste Term fast die Feinstrukturkonstante \alpha. Wir haben aber ein h und keine \hbar. Darum müssen wir noch das Ganze mit 2\space *\space \pi erweitern.
\cfrac{1}{2\space *\space \pi}\space *\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space h\space *\space c}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2\space =\space \bigg(\cfrac{1}{2\space *\space \pi}\bigg)\space *\space \alpha\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Das waren alles sehr einfache mathematische Umformungen. Wenn wir wissen wollen, was dies Aussagt, so müssen wir mit dem Rechnen aufhören und zu einer Erklärung übergehen.
Rollen wir das Feld von hinten auf und fangen mit dem Term (\frac{m_P}{m_e})^2 an. Das Quadrat entsteht, da wir beim Kräftevergleich die Kraft zwischen zwei Objekten in der jeweiligen Raumzeit vergleichen. Daher müssen wir hier ein Quadrat setzen. Warum steht hier die Planck-Masse im Zähler und die Ruhemasse des Elektrons im Nenner. Beim Kräftevergleich haben wir das umgekehrt gemacht. Beim Vergleich der Kräfte, ist die Kraft aus dem elektrischen Feld viel größer, da sich die Elektronen in Ihrer Raumzeit wesentlich einfacher beeindrucken lassen. Wenn wir das Verhältnis auf die Raumzeit selbst anwenden, dann ist natürlich unsere Raumzeit viel stärker/zäher als die 2D Raumzeit. Daher muss das Verhältnis umgedreht werden.
Die Feinstrukturkonstante \alpha fangen wir uns ein, da wir einen Kräftevergleich zum elektrischen Feld machen. Die exakte Erklärung kommt im Teil 3. Hier mal die Kurzfassung: verhält sich so, wie eine Maßstabsanpassung in einer Karte. Der Maßstab muss einfach um \alpha gekürzt werden. Da die Planck-Masse festgelegt ist, kann sich \alpha nur noch auf die Lichtgeschwindigkeit beziehen. Da die Lichtgeschwindigkeit nicht von der Anzahl der Raumdimensionen abhängt, Langenkontraktion und Zeitdilatation treffen immer nur die Bewegungsrichtung ohne Berücksichtigung der restlichen Raumdimensionen, so muss der Bruch aus \frac{l_P}{t_P} mit Werten erreicht werden, die um \alpha verschieden sind.
Die Lichtgeschwindigkeit ist ein Bruch und kann mit unendlich vielen Werten erreicht werden. Da die Lichtgeschwindigkeit c aber der Dimensionale Übergang ist, muss \alpha bei jeder Wechselwirkung mit einer elektrischen Ladung mitspielen. Bei mehrfachen Wechselwirkungen mit einem Exponenten. Dies schauen wir uns im Teil 3 genauer an.
Die 2\space *\space \pi sind für uns alte Bekannte aus der Feldgleichung. Wenn wir in unserer Raumzeit mit einer Kraft arbeiten, dann brauchen wir diese je Raumdimension. Da wir bei einer Kraft immer eine Verbindungslinie zwischen den Objekten haben, kommen hier die 2\space *\space \pi nur einmal vor. Da wir das Verhältnis umgedreht haben, brauchen wir diese hier mal im Nenner.
Das war ein längerer Abschnitt zu Ruhemasse, Maßeinheiten und „Zähigkeit“ der Raumzeitkonfiguration. Diese kleinen Anmerkungen dienen dazu, das Thema mit dem Dimensionalen Übergang besser zu verstehen. Wenden wir uns am Ende des Kapitels ein komplett anderes Thema zu.
Als letzten Abschnitt wollen wir uns eine bestimmte Auswirkung aus den Grenzen der Raumzeit anschauen. Wenn an der Idee mit der sehr harten Grenze der Raumzeit etwas dran ist, hat der größte Teil aller anderen „Theory of Everything (ToE)“ oder Auslegungen der Quantenmechanik ein großes Problem. Diese funktionieren fast alle nicht mehr.
Wir können die Lösungsansätze des Mainstreams an diesen Theorien in vier Kategorien aufteilen:
In den vier Kategorien gibt es nicht die eine Theorie. Es sind immer ganze Familien an unterschiedlichen Theorien. Wie viele unterschiedliche Familienmitglieder es gibt ist für uns nicht relevant. Wir können in der DP für jede dieser Kategorien ein Argument finden, warum dies nicht funktionieren kann. Damit ist schon klar, wo der Beliebtheitsgrad der DP bei Physikern steht. Wir können wohl über 95% aller Ansätze ausschließen, für die diese Physiker in diesem Bereich ein Forschungsauftrag erhalten. Hier heißt es, gute Miene zum Bösen Spiel. Hier geht es nicht darum andere Theorien als „schlecht“ zu kennzeichnen. Wenn wir diese Theorien ausschließen können, dann haben wir Prüfungen für die DP gefunden. Die grundsätzlichen Merkmale dieser Theorien sind harte Prüfungen für die DP. Wir gehen einfach die Kategorien durch.
Hier haben wir gleich zwei Totschlagargumente, warum dies nicht mehr funktionieren kann. In der DP ist die Energie auch der Bewegungszustand. Damit muss die Raumzeit zwei zwingende Eigenschaften aufweisen: kontinuierlich und differenzierbar. Sonst können wir keine Bewegung als Raumzeitgeometrie direkt in der Raumzeit abbilden. Eine Raumzeit in Quanten ist damit nicht möglich. Insbesondere sind bei allen anderen Theorien die Raumzeit und der Inhalt der Raumzeit getrennte Beschreibungen. Die Raumzeit wird nur als „Hintergrund“ benutzt. Dann könnte man sich noch eine Quantelung vorstellen. Wenn die Bewegung aber eine Geometrie der Raumzeit selbst ist, funktioniert dies nicht mehr.
Das zweite Argument ist die Grenze selbst wie wir diese in der DP definiert haben. Das kann nur die Lichtgeschwindigkeit und ein Schwarzes Loch sein. Wie soll da die Raumzeit, meist auf Länge der Planck-Skalen, in Stücke zerlegbar sein. Dann ist jedes Raumzeitquant entweder mit Lichtgeschwindigkeit unterwegs und kann keine Zeit mehr feststellen oder es ist ein Schwarzes Loch. Beide Varianten können wir getrost ausschließen. Eine Quantelung der Raumzeit ist mit dem Ansatz der DP nicht möglich.
Was wir mit der Grenze der Raumzeit machen, ist das wir komplette Raumzeiten sehr hart voneinander trennen. Eine einzelne Raumzeit ist für uns ein Stück/Objekt. Eine einzelne Raumzeit könne wir aber nicht weiter zerlegen.
Sollte jemals eine Quantelung der Raumzeit festgestellt werden, ist die DP falsifiziert.
Hier müssen wir für den Bereich der Kosmologie und der QM etwas vorgreifen. Wir werden dort feststellen, dass es Austauschteilchen nur zwischen Raumzeiten geben kann, die in mindestens einer höherdimensionalen Raumzeit eingebettet sind. Austauschteilchen können wiederrum nur Abbildungen in einer eingebetteten Raumzeit sein. Die Raumzeitkrümmung ist explizit eine Beschreibung in der eigenen Raumzeit. Durch die Raumzeitkrümmung wird die Raumzeitdichte nicht verändert. Damit auch keine Veränderung der niederdimensionalen Abbildungen. Wir bekommen für die Raumzeitkrümmung keine Abbildung über eine Raumzeitgrenze hinweg. Zur Erinnerung: Der Übergang liegt immer in der Raumzeitdichte und nicht in der Raumzeitkrümmung. Wir können mit unserem Ansatz die Gravitation nicht in Quanten zerlegen.
Sollte jemals eine Quantelung der Gravitation festgestellt werden, ist die DP falsifiziert.
Eine Viele-Welten-Interpretation der QM klingt doch sehr stark nach der DP. Wir haben getrennte Raumzeiten. Wir haben so viele Raumzeiten wie Möglichkeiten. Das machen wir in der DP doch auch. Auf der Ebene der Schlagwörter ist dies alles richtig. Im Detail machen wir in der DP was komplett anderes.
Eine Vielzahl an Raumzeiten haben wir immer nur über die niederdimensionalen Raumzeiten. Wenn unser Universum eine 3D Raumzeit ist, dann wird bei einem Messprozess in der QM aus einer Menge von 2D Raumzeiten eine exakte Auswahl getroffen. Diese Abbildung aus 2D erzeugt über die niederdimensionale Grenze eine Wirkung in unserer Raumzeit. Wir erzeugen bei einem Messprozess keine gleichdimensionalen Welten. Wir reduzieren aus allen 2D Möglichkeiten auf die eine, welche die Wechselwirkung durchführt. In der Kosmologie werden wir dann noch sehen, dass eine 2D Raumzeit von unserer 3D Raumzeit sehr stark verschieden ist. Die Idee, es gibt mich in einem anderen Universum, wo ich die DP als Unsinn deklariere, haben wir nicht. Mich gibt es in unserem Universum nur einmal und in anderen 3D Universen bin ich nicht vorhanden.
Mit dem Higgs-Boson werden wir auch in der DP eine unendliche Anzahl von 3D- Universen erhalten. Diese erzeugen sich aber nicht durch eine Messung oder ähnliches. Die sind mit dem Urknall aus unserem Universum bereits vorhanden und können nur über das Higgs-Boson kommunizieren.
Sollte jemals eine Viele-Welten Interpretation festgestellt werden, ist die DP falsifiziert.
Hier haben wir eine ähnliche Situation. Wir behaupten in der DP, dass es niederdimensional und höherdimensional explizit gibt. In der Stringtheorie haben wir, je nach Ausprägung, eine unterschiedliche Anzahl an Raumdimensionen. Dann gibt es die AdS/CFT-Korrespondenz. Dort ist die Gravitation eine Raumdimension höher abgebildet als die Teilchen der QFT. Die Schwarzen Löcher im niederdimensionalen müssen in der DP auch eine AdS-Raumzeit sei. Sieht verdammt ähnlich aus. Letztendlich werden wir für die Abbildung eines Neutrinos ein Gebilde mit genauer einer Raumdimension haben. Das ist doch ein String!
Ich finde es erstaunlich, wie viel Ähnlichkeiten bei bestimmten Teilaspekten zwischen den verschiedenen Ansätzen der jeweiligen Theorien auftauchen. Die Theorien aber doch grundsätzlich unterschiedlich funktionieren. In der DP können wir mit jeglicher Version einer Stringtheorie nichts anfangen. Dazu nehmen wir uns drei Punkte heraus.
Die DP und jede Form von Stringtheorie schließen sich gegenseitig aus.
Sollte jemals eine Variante der Stringtheorie festgestellt werden, ist die DP falsifiziert.
Sollte jemals ein supersymmetrisches Teilchen zu einem Elementarteilchen gefunden werden, ist die DP falsifiziert.
Sollte jemals eine kompaktifizierte Raumdimension gefunden werden, ist die DP falsifiziert.
Das waren jetzt sehr viele Punkte, die es zu bedenken gibt. Alles nur aus den Grenzen der Raumzeit heraus. Diese machen die DP erst möglich und schließen aber so gut wie alle anderen Ansätze aus.
Damit wollen wir dieses inzwischen sehr lange Kapitel endlich schließen. Als nächstes werden wir eine der wichtigsten Grundlage der Physik aufbauen, das Relativitätsprinzip.