
Everything consists of spacetime.
We will start with superposition. We will do this first because in many lectures, superposition is described as the most fundamental property of QM. The solution theorem for superposition will be used almost the same way for entanglement and probabilities. Even the big point of contention—local and non-local—can be easily explained with it. Therefore, we will describe the idea of mapping superposition in more detail.
Before we explain superposition via the DP, however, we should first discuss what is meant by superposition.
Mathematics is helpful for explaining superposition. Here, mathematics is easier to understand than logical explanations. We have a linear differential equation f(x), regardless of what it is supposed to be. This mapping has a solution L. Now it may be that R is also a solution of f(x). There may be several solutions. Then, according to a mathematical theorem, L+R is also a solution to the mapping. This always works for linear differential equations in QM. Important! The additional solution is not L or R, but L+R. The combination of the solutions is also a new solution. This does not only work with two different solutions. In QM, we often need an infinite number of solutions. This sounds very simple mathematically, and it is.
The entire QM is represented by linear differential equations. That’s a good thing. QM is very complicated. It is only because it is a linear representation that we can calculate anything at all. However, this also means that if QM is the correct mathematical representation, and we assume that it is because it has been confirmed so well, then this behavior must also occur physically. In the case of a somewhat abstract description, such as the spin of a particle, we have no problem with such a statement. Then an electron simply has a combination of spin up and spin down at the same time. That doesn’t keep us awake at night. The situation is different with states that are familiar to us. This is where Schrödinger comes in with his cat. According to QM, Schrödinger’s cat is both dead and alive until it is measured. That doesn’t sound so understandable to us anymore.
In my view, however, the location of a particle is the best explanation for superposition. For us, a particle can exist at exactly one point in spacetime. According to QM, this is not correct. The clearly defined location only occurs during a measurement. Before that, a particle can be in many places at once. Every location is possible. Perhaps with a very small probability, but the possibility exists. This means that when we send out a particle, e.g., an electron, directly away from us, it is only highly probable that it is traveling away from us in a straight line. However, it could also be to the left or right of the straight line, albeit with a lower probability. This does not mean that the particle has a definite location, and we simply do not know it until we measure it. The particle is present in all possible locations at the same time. We are not familiar with this from our everyday lives. Okay, we sometimes think we have put a key in exactly this place, for example, and it is not there. But that has nothing to do with quantum mechanics. In our everyday world and also in GR, an object is present in exactly one position. In QM, the particle has the position left L, center M, right R, and additionally together (L + M + R). Location is where we have the worst case scenario. If we do not choose a specific setup for an experiment, then a particle has the entire spacetime available as a possible location. The electron is simultaneously present throughout the entire universe. Based on this mathematical approach, superposition is difficult to understand purely logically.
With SR, there may be disagreement about the timing, distance, and energy, as these depend on the state of motion. But in SR and GR, an object is clearly located in one place. Without this property, we cannot make any statements about an object in GR. Where should gravity/spacetime curvature be aligned if the energy/spacetime density does not have a clear location? This is the fundamental problem with unifying GR and QFT. In QM, the superposition of all properties of an object is the basic structure of the description. This means that an object or an interaction is not local. This means that the properties and interactions do not have a unique position. In GR, all objects are local. They must have a unique position. Otherwise, gravity could not align itself, or momentum would have no clear direction.
The next problem is that QFT or QM do not explain superposition. The mathematical descriptions were chosen to correspond to the experimental findings. This is the usual procedure. This also happened with gravity. Einstein had the idea of geometric mapping in spacetime. The field equations were constructed to correspond to the physics known at the time. For example, a major change was made for energy conservation. The mathematical description then gave rise to predictions such as black holes, gravitational waves, etc., all of which have been confirmed without restriction. It was no different in QM. In order to explain the double slit and the hydrogen atom, QM had to be constructed as a linear description with superposition and probability. All other statements of QM, such as the uncertainty principle, were found purely through mathematical description and subsequently proved to be correct. No matter how crazy the statements may sound to our everyday world.
In GR and QM, it is not possible to specify why we must choose this representation. In GR, Einstein’s idea of a geometric representation in spacetime is still reasonably “suitable for everyday use.” Therefore, there are fewer philosophical points of contention to discuss here. The main topic is almost always how to understand spacetime itself. In 2026, the discussion of whether spacetime is fundamental or emergent is a hot topic.
This is much more difficult in QM, as the number of topics is much greater. This is because QM has undergone an almost purely mathematical development. There is no comprehensible general basic concept, such as a geometric representation in spacetime. From a philosophical point of view, everything in QM is therefore “questionable.” There is no clear logical basis. This leads to an almost unmanageable number of “interpretations” of QM. Let’s take the Copenhagen interpretation of QM as an example. This is already a collection of different interpretations. Here, it is taken so far that a particle between two points cannot be assigned a distance/path. Even the existence of the particle is not recognized until a measurement is made.
We want to resolve this dilemma. We will provide justification for everything in QM. First of all, we must reject the Copenhagen interpretation. In fact, the description of QFT with path integrals is a suitable mathematical representation based on the DP. The different paths exist and are also traversed. Just not in our spacetime.
Let’s look for a possible mapping of superposition in the DP. As always, we don’t have many options. For almost all topics in QM, it will boil down to a mapping in a low-dimensional spacetime. The crux of the matter is the interface between 3D and 2D. We always obtain two fundamentally different representations for a spacetime density. One in 3D, according to GR, and at the same time an infinite number of representations in 2D, according to QM. This means that we do not resolve the two incompatible representations of GR and QM into a single representation. This “single” representation is the actual desire in a unification of GR and QFT. We must retain these two representations and connect them across the low-dimensional boundary. This is how it will work.
To begin with, we have the same problem as GR with QM. Spacetime density in our spacetime has a unique position. This has to be the case, otherwise GR no longer works. This means that the electron in front of us, which we want to accelerate away from us in a straight line, does exactly what we would classically expect from a particle according to Newton. It is not to the left or right, but in the middle with a straight momentum towards the target. At first glance, this has nothing to do with QM. This is also only one side of the coin. The part from the perspective of our 3D spacetime.
We come to quantum mechanics because every 3D spacetime volume and spac-time density is nothing else, always has an infinite number of 2D spacetimes available for mapping. Spacetime density therefore always has two simultaneously valid descriptions:
With the infinite number of lower-dimensional spacetimes, we can place at least one straight line from any point in our spacetime into the spacetime density of the electron. Based on this idea alone, it is possible to reach any spacetime point in 3D via 2D. A spacetime density from 3D can thus reach a spacetime point even away from its 3D path. However, this is only possible via 2D.
Important: We have an infinite number of paths via 2D, from a spacetime density with its local volume in 3D, to every possible spacetime point in 3D spacetime. These paths all exist simultaneously in 3D. This means that they must influence each other in 3D. How exactly this happens is explained in the later chapters on mathematics and then represents the interference of possibilities. The 3D spacetime density still has a say in the matter.
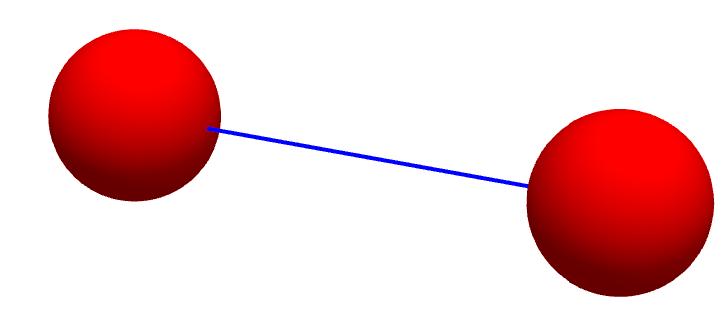
The straight line as a connection does not yet fit. Our spacetime is 3D, so the connection must be a 2D surface. We only ever go one spatial dimension deeper.
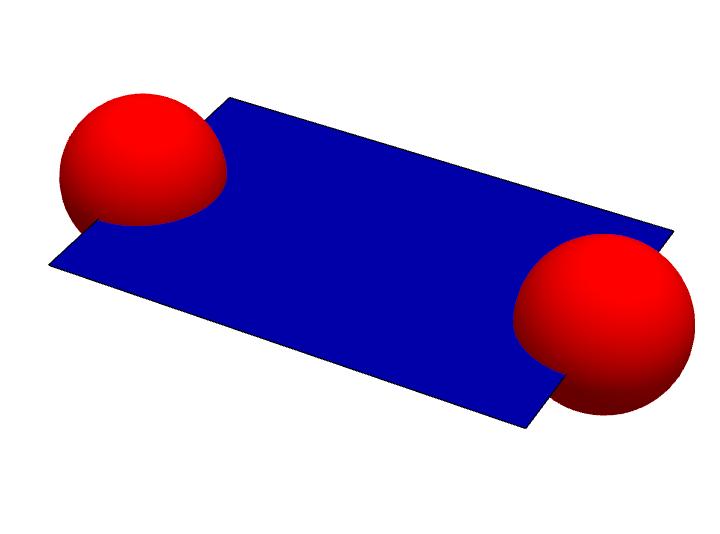
This is just one possible connection. If we rotate the surface between the two volumes around the connecting line, we can place an infinite number of 2D spacetimes between this distance. This alone allows us to reach all spacetime points in our spacetime. But that is still not enough. Who says that the 2D spacetime between the volumes has to be straight? There are many more ways to reach the points via an extrinsically curved 2D spacetime.
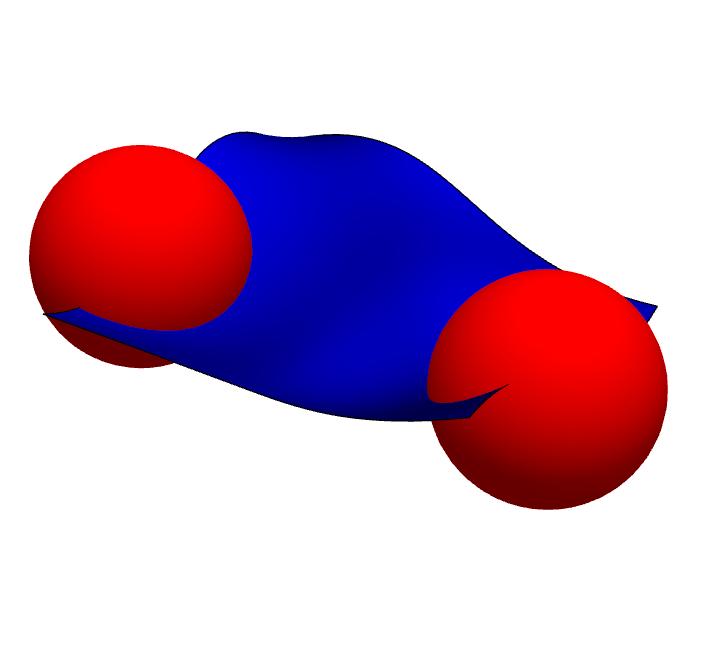
However, there is one important limitation. We only have one “type” of object available for a connection: spacetimes. All fields of QFT, and thus also the possible paths, are constructed by us using spacetimes. In DP, we have no other object available. In order for spacetime to be described by GR, spacetime must have certain properties. The two fundamental properties are: continuity and differentiability. For GR, we also need a certain “type” of differentiability, but this is not relevant here. These two conditions are mandatory in any n-dimensional spacetime.
We need continuity because otherwise we would obtain different spacetime boundaries. Spacetime must not have any “gaps.” Neither in 3D nor in 2D, otherwise there may be no connection.
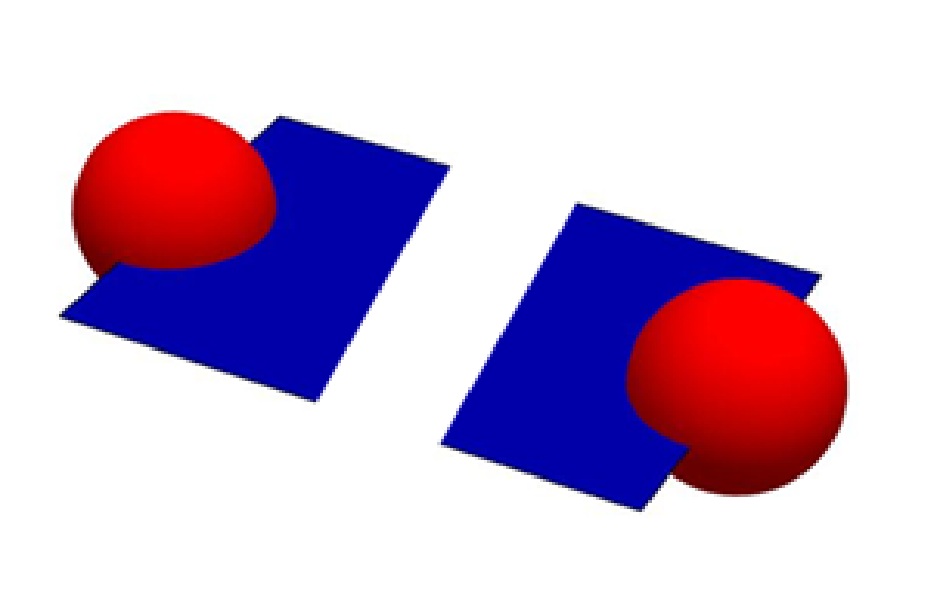
This is not how it should look.
In every spacetime, the image of a spacetime density always has a connection to every other point in spacetime. To repeat:
This means that the electron already has a connection to every possible spacetime volume in 3D. There are no boundaries within spacetime. Only the bridging of the distance deviating from the momentum is not possible directly in 3D. We do not need a description of QM for the straight path.
Through 2D spacetime, the electron has additionally gained an infinite number of paths to any given point in spacetime. However, only those paths that are continuous and thus uninterrupted may be counted. In fact, we will see later in the double-slit experiment that we cannot explain this experiment if we assume that an electron can “jump” directly from the source to the target (detector screen) without a path. Then it would not matter whether it is a double slit or not. Real “beaming,” as in Star Trek, from source to target is also not possible here. Paths must exist. However, the rule is that if I have at least one path in 3D, there are always infinitely many in 2D.
Differentiability is a simple mathematical term. It can best be translated as “round and connected geometry without corners and edges.” Here, a picture really is worth a thousand words.
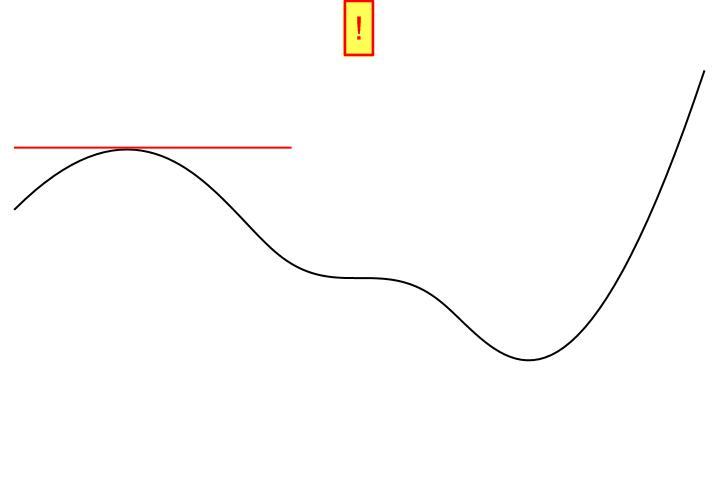
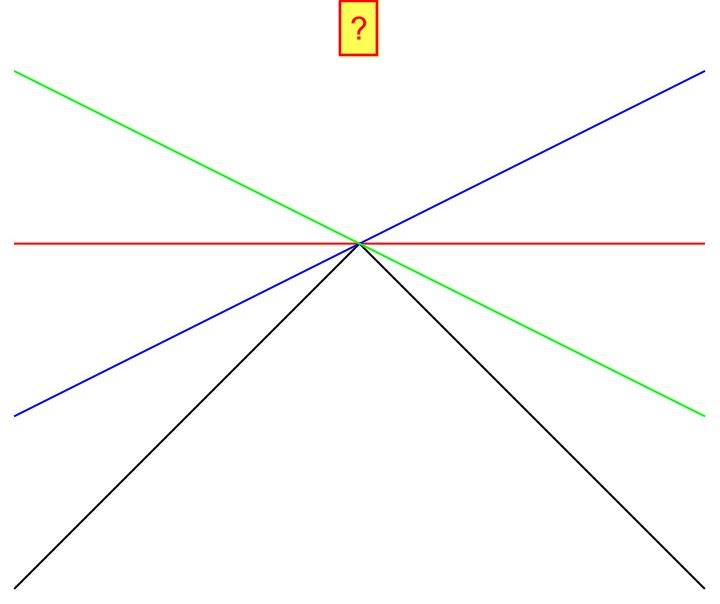
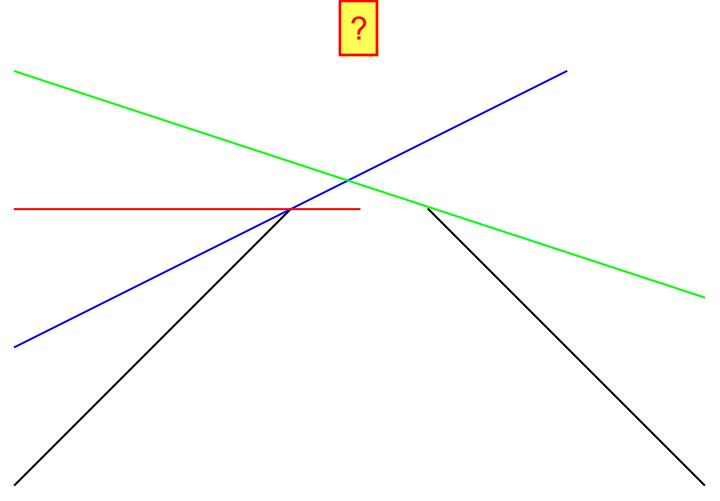
If you approach a specific point of a function from the left and from the right, you must be able to draw a unique tangent there. With a “smooth” function, this is always possible. With a function that has a corner or edge, this is not possible. There, you could draw an infinite number of tangents. This point is precisely where differentiation is not possible. Our argument of continuity also plays a role here. If there is a jump, we cannot draw a unique tangent at the jump. So much for simple mathematics.
Why is this differentiability so important to us? As a reminder, spacetime density is energy, geometry, and state of motion. Spacetime density is directly mapped in the geometry of spacetime. This also applies to the state of motion. The geometric mapping of a state of motion is differentiability.
No differentiability => no state of motion => no spacetime density => no spacetime. Spacetime density is spacetime itself. With non-differentiable spacetime, our approach would be useless.
This property is important again for mathematical representation. It influences the structure of the Schrödinger equation. In 3D, there are changes in spacetime, so we need to be able to differentiate twice. In 2D, everything is static. A simple differentiation is sufficient there. Since we can only allow “round” mappings, a wave description will explicitly be useful. Flat spacetime is the special case. But more on that in the chapter on mathematics.
A crucial question is: How do we bridge the distance in 2D? The answer is somewhat different than we would assume in the first step. In 3D, i.e., spacetime with spacetime density, the answer is momentum (directed spacetime density). Even if a certain amount of time is required to bridge the distance in a 2D or 1D spacetime, no time passes across the interface. Therefore, the process can take as long as it wants. In our 3D spacetime, every low-dimensional process will always happen instantaneously. We only know time in our spacetime. However, we have to use 2D spacetime specifically for QM. There, all images are static. We already had this in cosmology. How can an image, e.g., as a black hole, bridge the distance in 2D if there can be no change in spacetime?
Anyone who wants to invest 2–3 minutes here and come up with the solution themselves has understood the basic idea of DP.
The black hole or the extrinsic spacetime curvature in 2D does not have to bridge the distance at all. Again, every n-dimensional spacetime density is the n-dimensional spacetime itself. If 2D spacetime connects the destination and source in 3D, then everything needed for bridging is already present with a spacetime density. Spacetime and thus a spacetime density in 2D connects the locations in 3D simply by its existence. Whether the 2D spacetime itself has an extrinsic deformation or an intrinsic deformation as a black hole is irrelevant for the connection. With these deformations, the connection/spacetime only maps the properties of the particles. However, the existence of the particles is spacetime itself. It does not matter where these properties lie on the “path.” We cannot recognize any geometric quantities such as distance/length, etc. from low-dimensional.
Only two properties are important.
This means that flat 2D spacetime drawn in the first images cannot be recognized in 3D without a black hole. More on this later in the standard model.
However, from this bridging of a distance in 2D, we can make a demand on QM. All recognizable interactions from 2D to 3D must always and without exception occur instantaneously. If an interaction has a delay, this part always originates from our spacetime. We will revisit this in the context of entanglement.
If we obtain an infinite number of images as spacetime density in 2D from a single spacetime density in 3D, do we not then have a miraculous increase in energy? No, fortunately not. In DP, energy conservation remains valid. However, only separately for each spacetime.
In fact, this topic is not so easy to answer; it has many different facets. This is the description of the interface between 3D and 2D. This is exactly what the entire Part 3 is about. Therefore, we divide this into two areas. For the first area, the specification of energy, the answer can be found in this section. For all other open questions on this topic, and there are quite a few, we will explain this in the respective sections in Part 3.
Energy cannot be transferred across the dimensional boundary because time cannot be transferred. Energy can only be explained in relation to a specification of time, hence:
Spacetime density = energy = spacetime geometry = state of motion. A specification without time is not a complete representation in spacetime geometry or the state of motion. Without time, there is no energy. This means that, from the perspective of 3D, no energy is transferred from 3D to 2D. In 3D, spacetime density remains exactly what it is. Spacetime density in 3D does not emit energy into 2D spacetime.
What does it look like in 2D? It depicts spacetime density and thus also energy. Yes, that’s right. But the energy only exists to a limited extent in this spacetime, as an additional representation of the 3D spacetime density. The representations in 3D and 2D are based on the same energy, without 3D having to transfer energy to 2D. This means that this principle can be applied an infinite number of times. The mere existence of a 2D spacetime is a spacetime density and thus an energy. However, it does not count as energy in 3D. To do so, the 2D representation must bridge the boundary to 3D and thus enter quantization as an effect in 3D and not directly as energy. We describe this in more detail in quantization. We will take a closer look at what the individual representations look like in 2D in the standard model.
So, could we already be done with superposition? Superposition arises because we have an infinite number of 2D images at the same time. However, the word “simultaneously” should be used with caution here. In QM, just as in relativity theory, there is no longer any simultaneity. In relativity theory, this is due to the maximum speed of light. In QM, there is not even a temporal reference between the different spacetimes. This will become important later when we discuss the double-slit experiment. First of all, nothing has ever changed backwards in time. There is no forward or backward between spacetimes.
However, there is a second aspect to superposition that is important here. Superposition also exists for properties that do not relate to location. If we want to have superposition everywhere and in all properties, then the individual 2D image must also have a special geometry. To stay true to the example with location, we will describe this using an effect that only exists in QM, the tunnel effect.
The peculiarity of the geometric mapping in a single 2D spacetime is beautifully described by the tunneling effect. Let’s take our electron again, which we shoot away from us in a straight line. We place an obstacle in the path of this electron. The obstacle does not need to be a structure made of rest mass, such as a thin wall. A strong electric field that a charged particle cannot pass through is also sufficient.
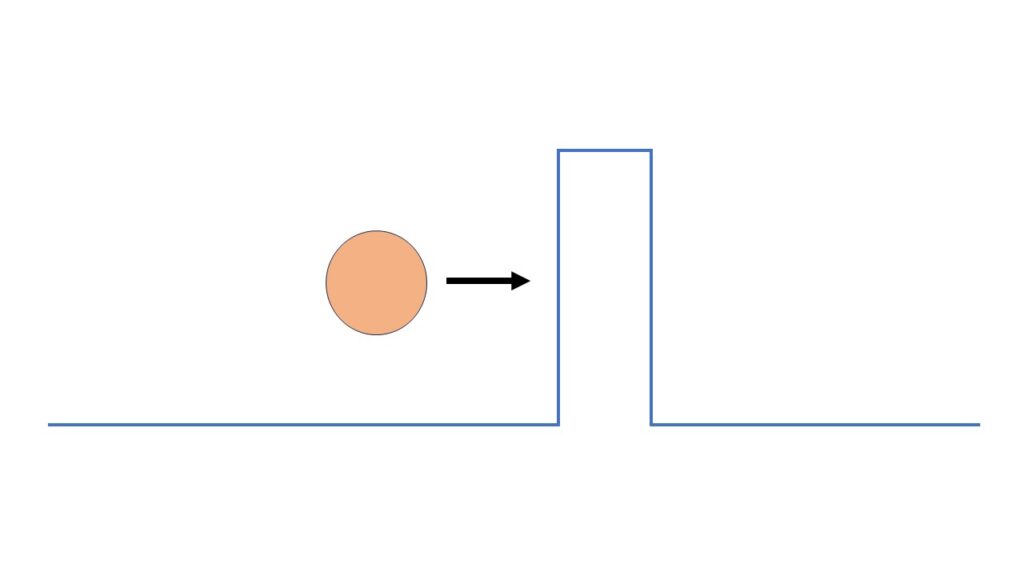
Our expectation is that the electron will not make it through the wall. This is also the description of classical physics. In QM, the electron may, albeit with only a small probability, pass through the obstacle to the other side. The reason for this should now be clear to us.
We simply map everything as geometry in continuous and differentiable spacetime. It follows that a “digital” mapping is not possible, even though we are talking about quantum mechanics. The spacetime density of the electron and the obstacle must not look like this.
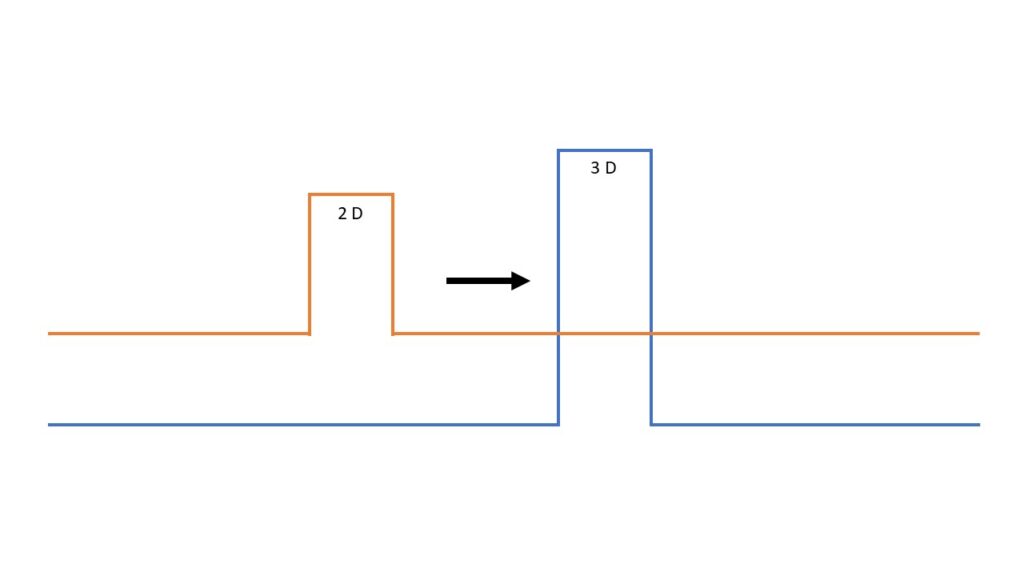
Both objects always look the same in 3D as well as in 2D.
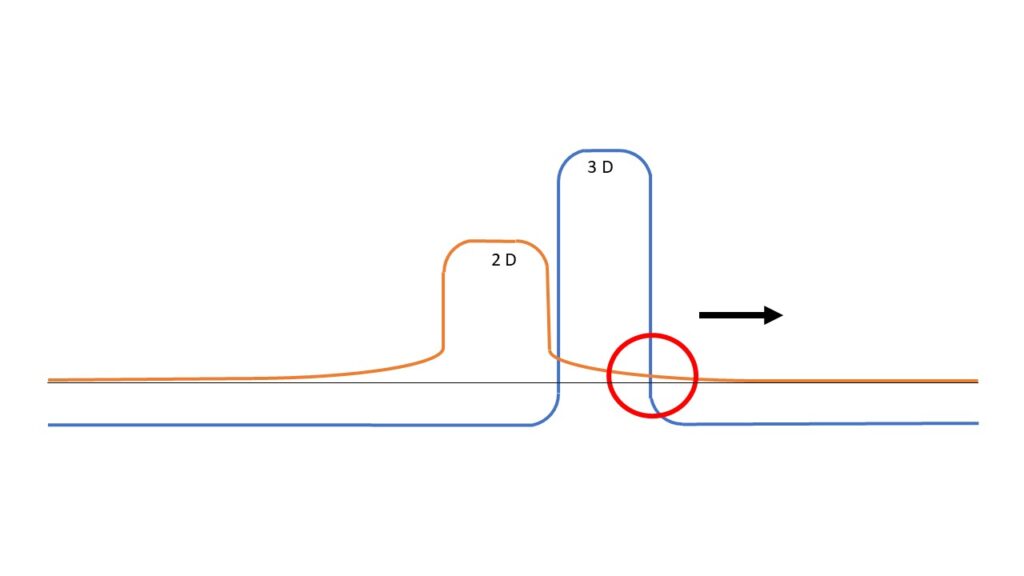
This wave mapping therefore always has the two properties that are most important for tunneling.
If you like, the term quantum mechanics is completely wrong from the perspective of geometric mappings. The mapping must not be quantized. We always create a possible overlap of the geometric mappings. This is the red circle, which lies behind the obstacle. We will discuss how we measure the electron there later. We will discuss interaction and measurement in a separate chapter.
However, the distance can only be bridged in 2D. In 3D, the obstacle blocks the spacetime density. This is the experimental setup. This allows us to demand that the tunnel effect must always happen instantaneously. In addition, the tunnel effect and superposition must be present for all properties of a particle. We map everything using the geometry of spacetime. This means that superposition and the tunnel effect do not only occur with momentum or location. However, we can illustrate this very clearly here. As we will see later in the chapter on the mathematics of QM, continuous and differentiable spacetime is the reason for the wave descriptions.
Superposition arises because we have an infinite number of low-dimensional images that condition each other in 3D. Each individual mapping stands alone in 2D. In 3D, however, all mappings are together. Therefore, the solution is not L, M, and R individually, but also L+M+R together in 3D. Our measurement always takes place in 3D. Therefore, the behavior of a superposition may be present until the measurement. After that, it is no longer present.
The big problem of locality does not exist in DP. In every n-dimensional spacetime, the spacetime density is always local. In 2D, an infinite number of images are present in 3D at the same time. This means that no local behavior may be present in QM. Local and non-local are only the different “dimensional manifestations” of a single spacetime density. This only becomes a problem if we want to map both sides of the coin in a single spacetime. However, according to DP, this is not possible. In DP, the question of locality in a spacetime is already wrong as a question.
In fact, there is one object that already exhibits clear local behavior in 3D without 2D: the black hole. Since the spacetime density at the center of the black hole cannot have a low-dimensional image, there is no superposition here and therefore no non-local behavior. This can also be seen in Hawking radiation. If the black hole and thus the event horizon did not have a unique position in our spacetime, no Hawking radiation could form. This is because the incoming and escaping particles would statistically balance each other out if the boundary fluctuated. Hawking radiation only works if the GR part of the equation remains local and the quantum fluctuations do not. This behavior can only be explained if the black hole with its event horizon has no quantum mechanical image.