
Everything consists of spacetime.
GR is based on only 3 principles
We have already derived the principle of relativity and the speed of light in the chapter on SR. For GR, the principle of equivalence is still missing. There are two of these: the weak and the strong principle of equivalence. We will treat both separately. The strong principle is sufficient, as it includes the weak principle. Hence the names chosen. The separate derivation is interesting for the logical structure. The astonishing result of the derivation is that spacetime itself is a potential field. This becomes very important again in cosmology, in a different form. In GR, the vector potential field of spacetime is identical to the potential field of gravity. All other potential fields in physics function according to the same principle. In QM, they do so in different spacetime configurations.
In addition, in this chapter we will clarify what a force is in the classical description of physics. This helps in understanding gravity. Einstein’s ingenious idea of a force as a geometric mapping in spacetime is not always immediately understandable. We then find it easier to see why we can use such different descriptions for an identical phenomenon.
Let’s start small, then we can build on it. The weak equivalence principle is already contained in Newton’s good old mechanics. In classical mechanics, however, it was unclear why this is so. Here, the principle is often referred to as the equality of inertial and gravitational mass.
What E\space =\space m^2 is to Einstein, f\space =\space ma is to Newton. The two most famous formulas in the world. Force is equal to mass times acceleration. Newton’s second axiom. The mass m in the formula is inertial mass. Inertial because it does not change its state of motion unless acceleration acts on it. The more mass there is, the greater the acceleration we must apply to achieve an identical change. No acceleration, no force, and therefore no change => inertia. Since mass is the only object in the formula, this inertia must be linked to mass. So far, so simple.
Same question as with SR. Why then is there the first axiom? Well, do you still know it by heart? Let me help you: “A force-free body remains at rest or moves in a straight line at a constant speed.” We already had that in the second axiom. No acceleration, no change. Why does this statement appear twice in separate axioms? Here is an argument without the principle of relativity. For this to make sense, we have to read the first axiom differently. We reverse the statement: if no forces act on a body, then what the body does is rest or move in a straight line at a constant speed.
The first axiom is also a measurement rule. We can measure what a straight and uniform motion is. In a spacetime with spacetime curvature, “straight” is not so easy to determine. This makes a popular statement about gravity questionable. A body in a gravitational field falls without force in a straight line toward the center of gravity. We will see that this statement should be treated with caution. Here we will learn the difference between a potential field and a force.
Newton’s next famous formula is the formula for gravitational force
F\space =\space \cfrac{G\space *\space M_{grav}\space *\space m_{grav}}{r^2}
The large M is supposed to be the Earth and the small m a test mass. The mass here is the gravitational mass. That is what the scales show. We put this formula together differently.
F\space =\space \cfrac{G\space *\space M_{grav}}{r^2}\space *\space m_{grav}
According to the units of measurement, the first term with the fraction is acceleration. For the Earth as M, this results in the familiar small g for the acceleration due to gravity. This gives us:
m_{inertial}\space *\space a\space =\space g\space *\space m_{grav}
If anything is to fit together here, we must be able to eliminate the different m or g and a. This brings us to the following statements:
The identity of inertial and gravitational mass was a mystery to Newton. We see that it must be so, but there was no reason for it. This identity has been verified very precisely in 2026. A deviation can only occur after the 14th decimal place. It is one of the most thoroughly verified values ever.
In DP, the approach is completely different. Every mass is a spacetime density. There is no characteristic for differentiation. All known characteristics for differentiation lie in QM and not in GR. This means that these characteristics cannot produce any difference when a “force” is exerted via gravity. We do not have to justify equality; it is necessarily given by the approach. We turn the tables. We do not even have the possibility of describing a difference.
If a difference is ever detected, no matter how far behind the decimal point, the DP is falsified.
Somehow there must be a connection between force and gravity as a geometric mapping. The strong equivalence principle refers to acceleration. In classical mechanics, this always generates a force. The solution is already contained in Newton’s axioms. First and second axioms: A force is a change.
In DP, we can understand classical force as a change in spacetime density. Without interaction, spacetime density remains what it is. Interaction can cause it to change. That is very simple. However, we have a big problem, especially with gravity. What is exchanged in an interaction? The long-sought graviton as the exchange particle of quantum gravity? No, definitely not!
In GR, there is only a geometric representation as spacetime curvature for gravity. All mass-energy equivalents are collected in the stress-energy tensor. In the Einstein tensor, we do not have spacetime density as an exchange particle. However, we still need a change in spacetime density. This is precisely where the strength of DP lies. We have curvature or density, but nothing more. It cannot be density. There is only one possibility left. The spacetime curvature must cause a change in the spacetime density without an exchange particle and without a change in the spacetime density. I know the sentence sounds a bit silly. But that’s exactly what I mean.
Ultimately, we have to come to the strong equivalence principle. There, gravity must not be distinguishable from acceleration in its effect on a mass. Thus, the curvature of spacetime must produce a change in the density of spacetime that corresponds to acceleration. The DP could also have been deduced if one wanted to fully explain the concept of a potential, in this case the gravitational potential. Unfortunately, people were already satisfied with the exact calculation. The reason why was no longer interesting.
For us, force is a change in spacetime density. Since spacetime density is also a state of motion, it should come as no surprise that force is associated with acceleration. Changing a state of motion requires acceleration. This clarifies the concept of force. Let’s move on and finally take a look at the strong equivalence principle.
In the strong equivalence principle, we cannot distinguish the effect of gravity from the effect of acceleration. Gravity and acceleration do not have to be identical; we just cannot distinguish between their effects.
We saw the first approach in the weak equivalence principle. There, a and g had to be identical. Einstein then came up with the idea that motion in a curved space must correspond exactly to this acceleration. As we can see from the word “effect,” it was already clear to him that this is realized with different phenomena.

We are back on the road with Galileo’s closed box. In SR, there was no external effect. Here, it is gravity or the acceleration of the rocket. In both boxes, we cannot determine whether it is gravity or acceleration with any experiment. The effect is identical.
Since the concept of spacetime deformation was not yet widely understood at the beginning of general relativity, the old analogy with acceleration was retained. In order to obtain an effect similar to acceleration, the test object m must “fall” into the center of gravity in curved spacetime. I believe that this analogy has slowed down the search for the “why” question. The moon falls toward the Earth. Since spacetime is curved, the moon falls in its orbit around the Earth. This can also be calculated very well. Everyone can understand this, and everyone is satisfied.
Not us! This analogy explains nothing. According to calculations in general relativity, the moon moves around the Earth on a geodesic. This term refers to the direction of motion without the influence of any force. In a spacetime without gravity, this is a straight line. With gravity, it is the almost circular orbit around the Earth. Force-free, which reminds us of Newton’s first axiom. In a flat spacetime, straight and uniform. In a curved spacetime, always following the curvature. But that is precisely the measurement rule that states that the moon is not subject to any interaction. No acceleration and therefore no change. Where is the effect of acceleration supposed to come from? The first axiom and the second axiom are mutually exclusive in the case of acceleration. In GR, however, it is assumed that both can exist simultaneously. The force-free moon (since it is on a geodesic) falls (and thus accelerates) around the Earth. No, that’s not how it works.
So, let’s calm down a bit and continue. There is no external interaction, and yet we still need a change. This change remains constant, for example in the case of the moon, over billions of years. This question has never been resolved. So, let’s do that now.
The first idea we can have is that the value of spacetime density changes in a spacetime curvature. Then we have no interaction from outside and still have a changed value. That sounds very much like the solution we are looking for. In the spacetime curvature, the length becomes larger and larger and the length of the spacetime density remains the same. Then, in relative terms, the density becomes larger and larger. This means that spacetime density undergoes a perpetual change = acceleration due to the environment. Yes, but we have a spacetime. In the time dimension, the opposite is true and everything balances out again.
Don’t be sad, that’s a good thing. We need energy conservation. Spacetime curvature does not change the spacetime density for its area. Remember the constant surface area. This means that the ratio of a spacetime density to the surrounding spacetime with spacetime curvature does not change either.
Ultimately, we have no interaction from the outside. This means that the ratio of the spacetime densities of the environment and the object cannot change. But we only have spacetime curvature and spacetime density, so where else could it come from?
The only thing that remains now are the shifts between the spatial dimension and the temporal dimension in spacetime curvature. Let’s take a closer look at this.
A spacetime density moves toward Earth at 1 m/s. Far away from Earth, this is a straight-line and uniform motion. Here again is the important note: spacetime density is always the state of motion. Since we have no external interaction, the speed must remain the same. No change in spacetime density is identical to the same state of motion. However, in spacetime curvature, space and time change their definition. The meter becomes longer, and the second becomes slower. But this only happens with the surrounding spacetime and not for the spacetime density. The speed must remain at 1 m/s. This means that the spacetime density must become faster. It now has to cover a longer distance in less time. The spacetime density is accelerated solely due to the opposite change in the space and time dimensions. Locally, the spacetime density is free of any force, as it does not change. This somewhat strange acceleration is exactly what we need:
The strong equivalence principle results from the opposite deformations of the spacetime components in a spacetime curvature. The spacetime density does not explicitly undergo any change or interaction. We obtain acceleration because the state of motion must not change. That is the joke of the equivalence principle according to the DP. Here we see again how important it is that this deformation is a change in definition and not just a point of view. The equivalence principle only works with a change in definition.
The change in the spacetime components can also have the opposite effect. This happens precisely when acceleration can no longer increase speed. We must consider the special case of the speed of light. Here we have two possibilities:
Let’s look at the following image:
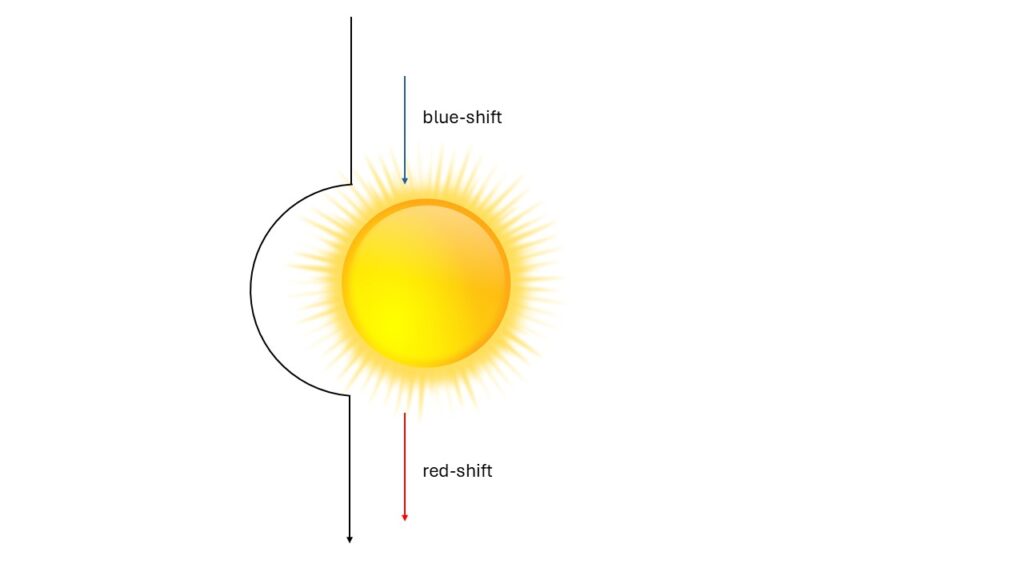
A photon traveling at the speed of light flies very close to the sun. As the photon flies toward the sun, it is blue-shifted. As it flies away from the sun, it is red-shifted to the same extent. Overall, there is no change in frequency.
However, the photon must follow the curvature of space. This results in a longer path for the photon. Then the longer path simply has to be traveled at the speed of light, and everything is perfect. This is what people thought until Mr. Shapiro discovered a deviation for light in the mathematics of general relativity. Light signals must have a lower speed when passing a mass. The effect has been experimentally confirmed to approximately 4 decimal places.
Even at the risk of boring you to death. Here, too, we see in the equivalence principle that the change in the spacetime metric must necessarily be a change in the definition of geometry. If this curvature were only a longer distance, this effect would not occur.
The photon has the maximum speed. In spacetime curvature, by definition, the distance becomes longer and the time shorter. Acceleration is not possible. In this environment, the photon slows down for an observer. Locally, the photon retains the speed of light, as we discussed in SR.
In fact, Einstein had already encountered a delay. But it was Mr. Shapiro who came up with the correct result. Einstein was missing a 2 in the formula. But it is important. We have a longer distance and a slowed-down time. Therefore, the delay is doubled.
Is there such a thing as anti-gravity, like the positive and negative forces in electricity? With gravity, everything is always attractive. According to general relativity, yes. That was a very surprising result from the mathematics of general relativity. Gravity has a repulsive effect when it becomes too strong. In mathematics, this is possible because GR is not a linear equation. It is rather difficult to understand this using pure logic alone.
This does not mean that gravity is cancelled out by the geometry of the object. The center of a hollow sphere has no gravity, even though it is surrounded by mass. Since gravitational force is a vector force, it cancels itself out at the center. If we use the Kerr metric instead of the Schwarzschild metric to solve the field equation, this also happens at the center of a black hole. The singularity is then not a point, but a ring in the center of a black hole. This is because the Kerr metric can map a rotating black hole. This is also the more exact solution. Due to the rotation, the singularity is not a point, but a ring. In the center of the ring, gravity is zero. Gravity toward the singularity is canceled out.
What we want is a repulsive effect, not a cancellation. According to GR, this repulsion exists at the center of a black hole, where gravity is very strong. This is why ideas keep cropping up that our universe is the center of a gigantic black hole. Since this is what mathematics indicate, it is simply assumed.
What does DP say about this? Since we want to confirm the mathematics of GR, except for the singularity, something like this should also exist. That is exactly what happens. With one crucial difference. Once again, we can clearly explain the reason for this “repulsion.” In DP, we only need this repulsion in the case of very high gravity, or rather, very high spacetime density.
Spacetime curvature is the reaction to spacetime density. This makes the space dimension longer and the time dimension shorter. For anti-gravity, we have to reverse this. The space dimension must become shorter and the time dimension longer. This happens for two reasons:
Spacetime is a continuum. This means that there is no boundary between spacetime density and spacetime curvature. They merge directly into one another. This is not a problem as long as the difference between spacetime density and spacetime curvature is not too great. The problem arises when we want to move from extreme spacetime density to extreme spacetime curvature. We have no problem with the time dimension. In both cases, the time dimension becomes shorter, and we already have a suitable transition. It is different with the space dimension. It becomes smaller with spacetime density and larger with spacetime curvature. Above a certain difference between these behaviors, the difference is greater than our dimensional constant d, which allows for change within a certain length. That does not work. There must then be a range between the spacetime density and the spacetime curvature where this continuously adjusts. We get anti-gravity from the spacetime curvature to the spacetime density. The spatial dimension becomes smaller and not longer. Since the time dimension also has to adjust, but actually already has the appropriate behavior, this adjustment is also only possible within a certain length.
We obtain anti-gravity shortly before the “singularity.” This is the desired behavior according to the field equation, and we now also know why this is the case. However, this only happens when we get close to d. The greater the spacetime density, the greater the area of transition with anti-gravity. We will not be able to detect anti-gravity in our solar system.
The final act for this chapter will be gravitational potential. In my opinion, the term “potential” is one of the least understood but most frequently used terms in physics for calculations. If it does not have to be 100% accurate, then we always calculate problems involving gravity using potential rather than directly using spacetime curvature. Otherwise, it is far too complicated. The trajectories of almost all objects that we have launched into space and will launch in the future have been calculated in this way.
If we ask a physicist what potential is, we almost always get something along the lines of: Potential is the ability to convert potential energy into kinetic energy. Okay, where does this ability come from? Is it inherent in the body? Everyone agrees that this ability lies in the potential and not in the body. The identical body outside of a potential does not experience acceleration. So, what is this ability? Usually, there is a pause. Often the answer is: a property of the potential. We are back to square one.
For almost all potentials, it is important whether the test body participates in the interaction of the potential at all. A neutral neutrino is completely unaffected by an electric potential. With gravity, we have the peculiarity that absolutely everything we can identify as an object participates in the gravitational potential. This makes sense, since in DP everything is a spacetime density in curved spacetime and must therefore participate. With the other interactions, the geometry in QM determines whether an interaction may take place.
We have another special feature. The “internal structure” of the object with the appropriate charge for the potential is irrelevant. Whether an electron as an elementary particle with an elementary charge of 1 or a composite proton that is almost 2000 times heavier with an elementary charge of 1 participates is irrelevant for the effect. It is only about the elementary charge of 1. In gravity, however, particles that have no charge, in this case no mass, also participate, e.g., the photon. It is about the deviation of the length dimension from the time dimension. This is always zero in spacetime density, since the space and time dimensions deform identically. The deviation comes solely and exclusively from the environment with spacetime curvature. This will also be the case for other potentials, such as the electric field.
If we want to get out of a gravitational potential, we have to counteract this acceleration. We need a rocket. The acceleration is not just an apparent effect. A rocket must deliver sufficient power to successfully counteract this acceleration. This time, we apply a force to the rocket via interaction, which actually increases the spacetime density. The state of motion of the spacetime density (rocket) and thus the energy itself must be increased to escape velocity by acceleration.
Acceleration converts kinetic energy into potential energy. This is the classic statement about gravitational potential. In fact, nothing is converted into potential energy. The rocket must generate acceleration against gravity through interaction. The rocket leaves the gravitational potential and then has a higher state of motion outside the potential.
Calculating the potential is very simple. Energy conservation results because the mutual accelerations must cancel each other out. The energy of the rocket has actually increased. The potential is simply assigned to negative energy. However, the object, our rocket, has actually increased its spacetime density when leaving the potential. This is all lumped together in the calculation. Negative energy in the potential gives us energy conservation and the calculations are very simple.
How does this work in the special case of light? Let’s look at a photon in the wave description, as this is somewhat simpler. The photon does not necessarily have to slow down; it can do something else. If the energy of a photon is determined by its wavelength and acceleration corresponds to an increase in energy, then the photon can increase its energy at the same speed by means of a smaller wavelength. This is the blue-shift. If the photon wants to escape from the gravitational potential, the opposite happens and we get the red-shift. It has to use part of its existing spacetime density to counteract the acceleration of gravity. However, this only works into or out of the potential.
This clarifies where the equivalence principle comes from. To summarize again in a few short sentences:
This brief explanation should now make it clear why Lagrange and Hamilton work so well. It all comes down to the conservation of energy. Spacetime density can only transform itself. Spacetime density cannot decrease or increase itself; this is the conservation of energy. With this knowledge, we can turn our attention to cosmology: the evolution of our universe.