
Everything consists of spacetime.
In this chapter, we will derive the most important conclusion from the assumption of spacetime density. Our spacetime, and every other spacetime, has boundaries. From these boundaries, we deduce that there are an infinite number of spacetimes in different configurations. The definition of spacetime density is also described in detail here. The importance of this topic cannot be overstated. The entire field of cosmology and quantum mechanics depends on this topic. Without understanding the boundaries of spacetime, there is no point in even starting the subsequent chapters. Therefore, read this chapter when you have time and peace and quiet. The other ingredients, besides time and peace and quiet, are up to you. I suggest gummy bears and a glass of wine. You may want to read the chapter twice until you have grasped the basics.
Before we go through all the points in detail, here is an overview of what we need to discuss. The number and importance of the points already show you the high priority of the spacetime boundaries:
Some points may not be 100% fully developed. These will then be taken up again in the respective special topics. This mainly concerns the structure of spacetime. In particular, the interaction of different spacetime configurations is described in cosmology and QM.
How did we come up with the idea that spacetime has a boundary? Currently, in 2026, this question is considered unresolved in textbook physics. Based on our everyday experience, absolutely every object has a limited extent. At some point, an object ends and there is then another surrounding space for the object.
This is not the case with spacetime. The reason is simple. Spacetime defines what length or time is. That was our approach to spacetime density. This means that there is no valid definition of distance or time outside of spacetime. This definition only exists within spacetime. The definition may vary in different spacetime configurations, but without spacetime there is no definition of space and time. How then can we define the boundary of spacetime if there is no surrounding spacetime and therefore no “outside” of spacetime?
One possible solution: there may be other spacetimes in which our spacetime is embedded. In this chapter, we will learn that this is indeed the case. However, this environment is of no use to us at all for specifying a distance or time outside our spacetime. A spacetime defines length and time only for itself. From Newton to Einstein, space and time went from being separate objects with absolute specifications to a single object with dynamic behavior of space and time. We go one step further and will have the definition of space and time separately in each spacetime. This means that we can no longer assume that our spacetime defines a distance or time in any other spacetime. Again, each spacetime is its own separate object, which defines length and time only for itself. This will be one of the most important statements in this chapter. This means that we cannot set a boundary from spacetime with a specification of length, volume, or distance. We need another idea.
If we want to examine spacetime as such, then the best way to do so is to look at the deformations of spacetime. As already indicated in the assumptions, we cannot ultimately recognize anything else. How do we proceed? We have reintroduced spacetime density, so let’s take a look at its extreme values. For new objects such as spacetime density, it is always a good idea to examine these objects in their extremes.
We want to let the spacetime density approach zero. To do this, the time and space dimensions must let their definitions of length and time approach infinity. Time relaxation and length relaxation. We had defined these names as such. This “counter-deformation” to spacetime density will become important again in the chapter on cosmology. This will result in our expansion of spacetime (not just space).
We do not obtain a limit. The spacetime density decreases but will never become zero. We will clarify this in more detail in a later section. What is crucial for us here is that spacetime has no limit in this case. If this approach does not work for us, then we will try the opposite.
At higher energies, the time and space dimensions approach zero identically to their definitions. This means that the spacetime density becomes larger and larger and approaches infinity. If both dimensions approach zero linearly, the increase in spacetime density must be at least quadratic. However, the already larger spacetime density must be compressed further and further. Therefore, the increase in spacetime density is even exponential with linear time dilation and length contraction. Spacetime density is energy. This has been explicitly defined by our approach (source of gravity). Thus, with a linear increase in energy, the increase in spacetime density will become less and less. The proportion of the increase in total energy continues to decrease with the same amount of energy. Therefore, an exponentially growing amount of energy must be applied for a linear increase in space contraction and time dilation.
In addition, there must be an insurmountable limit to the “shrinking” of the time and space dimensions. Once we have reached zero in the definitions of the dimensions, that is the end. It cannot go any further. Before this limit, the spacetime density must tend toward infinity. In addition, a spacetime density that occupies all spatial dimensions cannot lose a spatial dimension all at once. This is present in spacetime. It must already be determined in the occupation of the spatial dimensions (“internal structure”/QM) whether this limit is reachable or not.
This allows us to obtain a boundary. This boundary behaves in a very peculiar way. The boundary can only be reached if at least one spatial dimension and the time dimension are not occupied by the spacetime density from the outset. If all spatial dimensions are occupied, neither the spatial dimension nor the time dimension can reach this boundary. This is a very strict switch for reaching this spacetime boundary.
What we need is now clear. An absolute boundary within spacetime that cannot be reached by certain objects and is the condition of existence for objects that lie on this boundary. We need time dilation towards zero and length contraction towards zero. We are familiar with this, namely the speed of light. Therefore, the speed of light, as the boundary of spacetime, is a change in the structure within spacetime. Every point in spacetime can experience this boundary. It does not have to be located at an edge. An edge, as with a normal everyday object, does not exist in spacetime. If we remove one spatial dimension, then we must be located at the lower-dimensional boundary of spacetime. Of course, the time dimension is then also zero. If we want to identify spacetime as a single object, then we can no longer have time when we leave spacetime. Space and time are a single object and therefore inseparable. Leaving a spacetime is thus caused by a structural change. Why we can still perceive an object (spacetime density) with the speed of light in our spacetime is another topic for this chapter. Here we want to note:
A spacetime has a boundary
According to the textbook, the speed of light c is, by postulate of SR, the fixed maximum speed in our spacetime, identical for all observers. This means that it has always been a boundary. What is so special about the DP’s view? This boundary is a special boundary. Let’s take a closer look at the speed of light.
As the name suggests, the speed of light is a speed. It is defined as \frac{Length}{Time}. The numerical value of the speed of light is purely arbitrary. We have defined it as one meter and one second, and thus the value of the speed of light. Since it is generally accepted that the speed of light is constant, physics reverses the definition. The speed of light is defined, and this results in a definition of the meter and the second. From the perspective of DP, the speed of light can be defined very simply. It is the speed at which time dilation and length contraction reaches zero. This means that the maximum deformation of spacetime for a given spacetime density has been reached.
Why do we obtain a specific value for the speed of light? It should be \frac{Lenght\space =\space 0}{Time\space =\space 0} for the object. This is an undefined mathematical expression and not a specific numerical value. Fortunately, our spacetime has more than one spatial dimension. The representation of the spacetime density of an object moving at the speed of light can therefore only exist in the other two spatial dimensions. A spacetime density must be represented there. But that is not enough. We can only determine a spacetime density as an object. Two spatial dimensions do not result in a spacetime density. The object (e.g., a photon) must have another characteristic for us to recognize this. We will explain this later in this chapter, but in a later section.
We already know that Planck length and Planck time define the speed of light. However, based on the definition, there are an infinite number of values for length and time. Speed is a fraction. It could also be, for example, only half Planck length and half Planck time. This boundary condition alone does not explicitly define Planck time and Planck length as the smallest possible units of length and time in spacetime. It is the combination, i.e., the fraction, that determines the speed of light. The important result for us is that there are objects that still exist in our spacetime at this boundary. Thus, this boundary exists for us.
The speed of light is a structural element of spacetime
There is no reason for a postulate of the speed of light as the maximum speed. We will discuss the second part of the postulate, its constancy for every observer, in the principle of relativity. The boundary as the maximum speed for (almost) everything in the universe results automatically from the approach of spacetime density. Since everything that exists is a spacetime density, every object is affected by it.
An observer recognizes (e.g., for a photon) a movement of spacetime density in the direction of motion with its time exactly at this limit. For spacetime density, which moves at the speed of light, this definition means something else. If an object exists that has mapped its spacetime density to only two spatial dimensions, then this object cannot perceive our 3D spacetime. One spatial dimension must be explicitly missing. But not just one spatial dimension. The time dimension is also missing. Like the spatial dimension, it approaches zero. In the previous interpretation of this fact, no special feature was seen in it. For us, this is different.
An observer recognizes (e.g., for a photon) a movement of spacetime density in the direction of motion with its time exactly at this limit. For spacetime density, which moves at the speed of light, this definition means something else. If an object exists that has mapped its spacetime density to only two spatial dimensions, then this object cannot perceive our 3D spacetime. One spatial dimension must be explicitly missing. But not just one spatial dimension. The time dimension is also missing. Like the spatial dimension, it approaches zero. In the previous interpretation of this fact, no special feature was seen in it. For us, this is different.
We change the space-time configuration from (-, +, +, +) to (-, +, +). In doing so, the time dimension also approaches zero due to time dilation, and the result is (+, +). This is no longer spacetime. There is no time dimension. We have thus left our spacetime. From this consideration, we draw our most important conclusion:
Our spacetime, and thus all spacetimes, have limits.
We can define these limits, separately for each spacetime, by stating that the time dimension must approach zero.
We already know one of these limits: the speed of light. This is the lower-dimensional limit. Due to length contraction, we lose one spatial dimension at the speed of light. This changes the spacetime configuration of spacetime and takes us out of our spacetime. This is where the analogy with a substance is incorrect. If you change the properties of a substance or an object, it is still the same object. Only with different properties. In spacetime, it is different. If we change the spacetime configuration, with one more or one less spatial dimension, then the time dimension is necessarily set to zero and we leave spacetime.
hen, for example, a photon is a real interface object of our spacetime. It lies directly on the boundary of spacetime. Only because the images of the spacetime density are present on the other two spatial dimensions can we recognize these objects at all. But then, if there is no interaction, only at the speed of light. For a photon, this is the condition of existence and not simply a speed.
Personally, I am very pleased to know that spacetime has limits and that one of them is the speed of light. A long, long time ago, when I was at business school, I had a physics teacher, Mr. Werner. He fulfilled 100% of all the prejudices and clichés about math and physics teachers. Unfortunately, Mr. Werner passed away while I was still at that school. Towards the end of the first school year, some of the class sat around a campfire drinking beer. It is important to me to emphasize that this did not happen during school lessons. Since I was already interested in physics, I asked Mr. Werner how he came to study physics and how he felt about it. He was not comfortable with quantum mechanics but found general relativity very elegant and beautiful. However, he had a problem with one aspect. This was not the singularity in general relativity, but the maximum speed. The principles of relativity and equivalence seemed logical and easy to understand to him. It was clear to him that all this only works if there is this maximum speed. However, the postulate of the speed of light seemed to him to be a “foreign body” in the theory. He would like to have a logical explanation for this.
Mr. Werner’s question has been on my mind ever since that evening and is one of the main reasons why the DP exists. With the approach of spacetime density and spacetime as an object/substance, this question is clarified. The speed of light is not a fixed speed limit. This necessarily follows from the approach. There is no “higher” state of motion than the speed of light. The time and space dimensions are zero. It cannot be any less. The definition of the speed of light must be reversed. It is not at the speed of light that time dilation and length contraction become zero. Reaching the low-dimensional limit of our space-time is the condition for the definition of the speed of light.
The low-dimensional limit is the speed of light
It’s great that I have found personal peace with the low-dimensional boundary. Does this insight take us further elsewhere? If I ask the question, yes. The low-dimensional boundary, or speed of light, can be chosen as an identical designation and explains the hard switch between objects with or without rest mass and what energy or mass is.
As we approach the low-dimensional boundary, spacetime density approaches infinity. We know this identical behavior from energy. This is no coincidence. In DP, we equate spacetime density and energy. This should be clear from the approach. We define spacetime density as the source of spacetime curvature. The source of spacetime curvature is any form of energy. Therefore, the identity between energy and spacetime density must necessarily follow. However, this allows us to explain what energy is. Energy is another term for the geometric definition of spacetime itself.
Energy is an identical expression for the geometric definition of spacetime = spacetime density
Here we have two different perspectives or units of measurement for an identical statement. To further deepen this consideration, let’s take Einstein’s most famous formula:
E\space =\space mc^2
The formula is correct. However, it is only so well-known because the formula in this form is very simple. The complete formula never had a chance to become so well-known because it is somewhat more complicated:
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
If the second term under the root is zero, we can take the root and end up back at the familiar part, the rest mass. For the second term to be zero, the movement, i.e., the momentum with p^2, must be zero. The speed of light c is constant and cannot be zero.
The first term corresponds to the rest mass. We will not go into this in detail now. To do so, we would need to have a complete understanding of the limits of spacetime. The description of rest mass will therefore come at the end of the chapter.
The part of rest mass that is of interest to us now are two ancient known facts.
We will therefore leave rest mass alone until the end of the chapter.
Let us consider the second term, momentum. In our approach, momentum must have a direct mapping in spacetime geometry. The whole thing with a direction. For us, this means that there must be a spacetime density with a distinguished direction.
For the colloquial term density, an excellent direction sounds a little strange. In a gas or liquid, density is identical in all directions. For spacetime, this is different. Here, we only have the definition of geometry for a description. Spacetime density always lies on the time dimension and on at least one space dimension. For a density in space and time, at least one spatial dimension and one temporal dimension must be involved. Spacetime density does not necessarily have to be mapped onto all spatial dimensions. We need at least one spatial dimension, otherwise the term spacetime density makes no sense. Therefore, different spatial dimensions can have different densities. Thus, momentum is a spacetime density with a distinguished direction in at least one spatial dimension. In the case of angular momentum, the direction is constantly changing, which means a constant change in geometry. We can determine this because an “internal force” must hold the object, e.g., a star, together against this change in direction. However, the spacetime density does not decrease when it remains in place or undergoes a shift in spacetime. It is only shifted to another “direction/spatial dimension.” Overall, however, nothing changes.
So far, we have equated the energy and geometry of spacetime. Now, momentum or angular momentum is also a form of energy. This means that there must be two different descriptions for the definition of geometry. A vector density as momentum and a scalar density as rest mass. But it’s not that simple. If the spacetime density characterizes a state of motion, then the rest energy must also have a state of motion. As the name suggests, this is not the case with rest mass. Okay, but then where does the motion point for a rest mass? In all directions at once. Then the motions cancel each other out and the rest mass has earned its name. We will see in the chapter on cosmology that this is the case, for example, with spacetime expansion. For a particle with rest mass, this mass must therefore come from the lower-dimensional interface, otherwise the spacetime density in our spacetime would cancel out to zero. Conversely, this means that the momentum must always lie in our spacetime. This means that the first term for energy comes from the lower-dimensional interface and the second term lies directly in our spacetime. We are narrowing down the definition of spacetime density. Here we can set the following condition:
Spacetime density is energy, spacetime geometry, and state of motion
Space and time have been combined into a single spacetime. We must do the same for these terms. These terms are different descriptions of a single object, spacetime density.
One more word about motion. The fact that the state of motion of an object is a geometry in the spacetime of the object itself can be described, without restriction, as unusual. We have to get used to this first. If not, all spatial dimensions change identically, we obtain motion in space. This is what we colloquially describe as motion. If all spatial dimensions change identically, this is a change in rest mass or its counterpart, spacetime expansion. In the case of spacetime curvature, with opposing changes in the components, this alters the movement in space and we obtain the “equivalence principle.” There is a separate chapter on this. The differences are explained again at the relevant point.
Based on our approach, the fact that we anchor motion directly in the geometry of spacetime should come as no surprise. Spacetime consists only of length and time. Spacetime must therefore be a representation of velocity. No other physical quantity can be constructed with only length and time.
With the current picture of spacetime density, it is very easy to explain why there are objects with rest mass and a state of motion below the speed of light and objects without rest mass and the exact state of motion of the speed of light.
For an object with rest mass, e.g., an electron, the spacetime density must occupy all three spatial dimensions of our spacetime. The speed of light is the low-dimensional limit of spacetime. Our spacetime then loses one spatial dimension. A given spatial dimension cannot simply disappear. It can only continue to increase in directional spacetime density up to the speed of light. The given scalar spacetime density, for example the rest mass for an electron, is continuously compressed in the direction of motion. This results in an energy that increases to infinity. Therefore, reaching the speed of light is impossible.
Space-time density with rest mass = 3 spatial dimensions are occupied
An object without rest mass must not occupy all 3 spatial dimensions under any circumstances. It may only occupy two spatial dimensions. This means that one spatial dimension is already missing due to the “internal structure” of the object. The object must not experience any acceleration. It must already be moving at the speed of light from the moment it comes into existence. No other state of motion is possible without interaction. The object lives in the low-dimensional interface of our spacetime.
Spacetime density without rest mass = 2 spatial dimensions are occupied
From this point, a test for the DP can be generated. If an acceleration phase to the speed of light is ever discovered for an object without rest mass, the DP is falsified.
But wait! Doesn’t the interaction with the Higgs field via the Higgs boson give the particles their rest mass? Not quite right! We can see this a little differently. In DP, the Higgs field must correspond to some form of 3D spacetime. In our view, the Higgs boson must be an exchange particle between several such “Higgs fields.” We will clarify this in Part 3.
This makes it clear that an object is either one or the other. Only in a “transformation process (interaction in QM)” of the object can the “internal structure (standard model of particle physics)” change. The spacetime density can be redistributed across the spatial dimensions.
Since at the speed of light, the space and time dimensions are already zero, no other spatial dimension can go to zero. The speed of light can only have one direction. From this point, a test for the DP can be generated. No object may have the speed of light in two directions at the same time. We can only set the time dimension to zero once.
We can derive the following conditions from the speed of light, which we equate with the low-dimensional limit:
With the speed of light, there is a lower-dimensional limit. Is there also a higher-dimensional limit? One more spatial dimension and no less. The condition for leaving spacetime is time dilation towards zero. This exists in only two places in the universe.
The condition that leads to a black hole must be the higher-dimensional limit. We are very familiar with this condition. If too much spacetime density (energy) is concentrated in too small length, it will turn into a black hole.
This condition, with its specific values, is already known. It is the reciprocal of Planck’s force. This is very cumbersome to use as a designation and in the unit of measurement as a force for an explanation. Therefore, we will define this limit differently and choose a more appropriate name. We will do this as we did with spacetime density.
Force of sovereign arbitrariness => Dimensional constant with the abbreviation d.
This gives the higher-dimensional limit a clear designation. We omit the word “higher” in the dimensional constant. The name “speed of light” is completely ingrained in everyone’s mind. We can no longer change this. The lower-dimensional limit cannot therefore be meant by the dimensional constant. Like the speed of light, the dimensional constant is one of the most important natural constants in our spacetime. It is also a structural element of spacetime and not a fixed value.
The speed of light is defined as c\space =\space \frac{Lenght}{Time}. For the dimensional constant, it is:
d\space =\space \cfrac{Lenght}{Energy}
If we add a length to a force (put on different glasses), we obtain the unit of energy. Therefore, for a reciprocal value of the force, the fraction in the denominator and numerator must be extended by a length. This representation is more suitable for explanations and is therefore used as a definition.
In both cases, it makes sense to have a length in the definition. A spacetime density always needs a spatial dimension in order to be able to be mapped in spacetime at all. Both limits are fractions, as they are divisions into a length. The length is in the numerator because we have to accommodate a length in time or energy for a spacetime density to make sense. This will become a general principle. The definition of a natural constant for our spacetime must always include a length.
Since the dimensional constant is again a fraction, the same statement applies here as for the speed of light. The length and energy do not specify a smallest length or a largest energy. It can again be half the Planck length and Planck energy. Only the combination of the values results in the dimensional constant.
The values are again known to us as Planck values. We cannot determine the values purely from the speed of light and the dimensional constant. These are two equations with three unknowns. One piece of information is still missing. We will obtain the missing information later in this chapter.
If one wants to give the dimensional constant an analogy, then it is probably a value for the resistance of spacetime to spacetime density. If this value is exceeded, the spacetime density is too high for our spacetime. Spacetime must enter a range that can withstand this value. This can only be a spacetime with one more spatial dimension. A spacetime with n+1 spatial dimensions is more difficult to deform than a spacetime with n spatial dimensions. We will need this principle in Part 3 for QM.
Our spacetime is already a damn tough piece of work. Small calculation (Note: All values for the Planck units are not reduced, i.e., not shortened by 2\pi):
Planck lenght =\space l_P\space =\space 4.051\space *\space 10^{-35} meters
Planck time =\space t_P\space =\space 1.351\space *\space 10^{-43} seconds
Plankc mass =\space m_P\space =\space 5.455\space *\space 10^{-8} kilogramms
Planck energy =\space m_P\space *\space c^2\space =\space 4.903\space *\space 10^9 joules
d\space =\space \cfrac{l_P}{E_P}\space =\space 8.262\space *\space 10^{-45} 1/Newton
\cfrac{1}{d}\space =\space 1.210\space *\space 10^{44} Reciprocal of d, Newton
No matter what spacetime density we want to use to trigger spacetime curvature, the spacetime curvature is lower by this factor. We have to accommodate a great deal of energy over a small length in order to bridge this value. This is the condition that leads to a black hole. Since we know c with the Planck length and Planck time, the only new value added here is the Planck mass. The Planck energy is calculated. These three Planck values thus determine the limits of spacetime. Here we have to reverse the definition again. The limits of spacetime are determined by these three Planck values and are therefore characteristic values for our spacetime.
Planck length, time, and mass are characteristic values for our spacetime
A black hole is the transition to a higher-dimensional spacetime that can map this spacetime density. Conversely, a lower-dimensional spacetime must have a smaller Planck mass. These different Planck masses for each lower-dimensional spacetime configuration will later be the different rest masses of the particles in the standard model of particle physics.
Each spacetime configuration has its own Planck values for the Planck units
Let’s do a little counter-calculation. If we consider d to be the maximum resistance of spacetime, then we should be able to calculate this in a simple way. Let’s use Newton’s formula for gravitational force:
F\space =\space \cfrac{g\space *\space m_1\space *\space m_2}{r^2}
If we substitute the extreme values for mass (Planck mass) and distance (Planck length) into this formula, then our maximum value must also appear. And so, it does. The reason for this will become clearer later when we discuss the constants of nature. If a statement about physics is to be stable, we often arrive at this statement in different ways. This is always a good sign of its accuracy.
F_{max}\space =\space \cfrac{g\space *\space m_P\space *\space m_P}{l_P^2}\space =\space 1.210\space *\space 10^{44}
In physics, there is what is known as the hierarchy problem. This is a name for the large difference when comparing gravity as a force with electromagnetic force. We did this at the very beginning. The value: 4\space *\space 10^{42}
This is a very large difference when considered as a force. However, we can easily explain this. All fundamental forces from QM always lie in the low-dimensional. We want to map the entire QM later. According to our logic, a low-dimensional spacetime must be much easier to deform than our spacetime. As we can see, the difference in the resistance of the respective spacetime is very large.
We repeat the calculation, but not with the rest mass of an electron m_e, but with the Planck mass m_P. Let’s pretend that a 2D spacetime has the same Planck values as our 3D spacetime. This results in a difference of only 0.00116140. We know this value as the fine structure constant α. However, this is only the case if we reduce α by 2\space *\space \pi. This was the additional term we used when comparing electric and gravitational forces. We will encounter these 2\space *\space \pi again shortly. The forces would then be identical except for α. We will discuss the fine structure constant in Part 3.
The hierarchy problem is simply the large difference in the resistance of spacetime configurations when there is one more or one less spatial dimension.
We found the two limits of spacetime by looking at the extremes of spacetime, and it has always been one of the big questions: “How can we imagine zero or infinity?” Mathematically, these concepts are now quite well understood. Physically, however, they repeatedly lead to “strange” ideas. We want to clarify this unequivocally. The result will be that within a single spacetime, neither a value of zero nor infinity can occur in the deformations.
Spacetime density is a density of spacetime itself. A spacetime density of zero therefore also means a non-existent spacetime. Let’s take a closer look at this. In our approach, spacetime density already results from the existence of at least one space and time dimension. Without a space dimension, there can be no representation as density. For us, this means that there can never be a spacetime point with a spacetime density of zero. This spacetime point then contains no extension on a space dimension and is therefore not part of spacetime at all.
We have used the term “spacetime point.” We will continue to do so. In physics, point sizes are often used in calculations. This simplifies the concept, and particularly the calculations. However, anyone who has read attentively up to this point should have gained the following insight:
There is no point in DP
The mathematical abstraction of a point is defined by the fact that a point has no explicit extension in any spatial dimension. This means that it is not part of spacetime. It cannot have any spacetime density. This also means that it has no definition of spacetime geometry, no energy, and no state of motion. Whenever we talk about a point in spacetime, a point mass, etc., this is a purely mathematical abstraction to simplify the problem or the calculation. In DP, there can be no point size of any kind. Let’s turn the argument around. It is not GR or QM that have problems with a point size, but rather the mathematical abstraction of a point has no real representation in physics.
We have only considered spacetime density. What about spacetime curvature? Can gravity become zero? From what we have discussed so far, theoretically yes. To do this, we need a spacetime with an absolutely homogeneous spacetime density. If there is no difference in spacetime density from one spacetime point (we continue to use this abstraction) to another, then there is also no spacetime curvature that needs to compensate for anything.
However, we live in a spacetime with varying spacetime densities, otherwise we would not be able to discuss this here. Spacetime curvature has an infinite range. If there is even one deviating spacetime density, then there is also spacetime curvature. This makes it clear that spacetime curvature is always present in our universe.
There is no compelling limit here yet. The speed of light implies that an infinite amount of energy is required to reach the low-dimensional limit. Can we get this from somewhere? A clear no. Here are three arguments:
No matter which side we come from. A single spacetime does not allow for infinite spacetime density or spacetime curvature.
GR is often criticized for predicting a singularity in the Big Bang or at the center of a black hole. This is only correct if one reduces the spacetime density to a point size or, in other words, does not know the limits of our spacetime. In the case of the Big Bang, this is the entire spacetime; in the case of a black hole, it is the mass of this object. In both cases, however, this is only a mathematical abstraction. Unfortunately, this circumstance is not included in the field equation of general relativity. In the Einstein tensor, spacetime curvature can be extended to infinity if a point size is assumed for the spacetime density. But then the spacetime density would have to be gone. A black hole in our spacetime always has a mass. The black hole is there, and so is the spacetime density that led to it. This means that a volume of spacetime density is always preserved at the center of a black hole.
There is no singularity in DP
The abstraction of a point has always caused problems. This is precisely where string theory comes in. Not a point, but the first mathematical “level” above the point, an object with only one spatial dimension, a string.
This gives us a very nice result for spacetime. Theoretically, spacetime density cannot have a value of zero or infinity. Theoretically, spacetime curvature cannot be infinite. Unfortunately, this is not included in the field equations. There could be a spacetime curvature of zero, but then there would be no deviating spacetime density in this spacetime, and it would therefore be “empty.” Empty here means that there must be no particles. Spacetime itself carries energy even without a particle. Its existence is sufficient for this.
We will take a closer look at the natural constants and Planck values used so far. Then we will add Planck’s constant h so that we can define our three Planck values of length, time, and mass, which have not yet been determined, with another equation. Here we are anticipating Part 3 a little. We will discuss the Compton wavelength in a moment. We will see that the quantum of action and the Compton wavelength follow from the low-dimensional limit of our spacetime and are not determined in the low-dimensional (QM). GR dictates this behavior to QM and not vice versa.
In textbooks, the three most important natural constants are always c, h, and G. In DP, we will shift this to c, h, and d. Then the gravitational constant G will no longer be relevant to us. We achieve this because G is composed of c and d. It makes sense that the gravitational constant G is generated from the boundaries of spacetime. The behavior of spacetime in the classical view with G must lie between the boundaries of spacetime. These boundaries are so far the only values determined by our spacetime.
Since G is a natural constant, it has not yet been derived. The term “natural constant” simply means that in physics, a proportionality constant is used in a formula about which we have no knowledge. No explanation for it means natural constant. We were able to derive c and d from the dimensional limits of our spacetime. If G is no longer to be a natural constant, we must be able to generate G from known (and, very importantly, derived) natural constants.
Since we are already working with Planck units, we will continue here. The gravitational constant is defined via Planck units as follows: G\space =\space \frac{l_P^2\space *\space c^3}{h}. We will jump ahead a little and specify that we can write Planck’s constant as h\space =\space l_P\space *\space m_P\space *\space c. This gives us G\space =\space \frac{l_p\space *\space c^2}{m_P}. We extend this fraction by c^2. Then we have the desired form:
G\space =\space \cfrac{l_P}{E_P}\space *\space c^4\space =\space d\space *\space c^4
The gravitational constant is composed of c and d. We can also explain why c and d must be used in this way. This means we must be able to explain why d is used without an exponent and why c must have the exponent 4.
The dimensional constant d creates a black hole and thus the higher-dimensional boundary for the entire spacetime. Regardless of the spatial dimension on which the spacetime density is mapped. If d is reached on any dimension, a black hole is created for the entire spacetime. Therefore, no exponent is required.
The speed of light c is independent for each spatial dimension. The momentum in one direction does not influence the other spatial dimensions. Length contraction only occurs in the direction of motion. Therefore, a c^4 must be used to consider the entire spacetime. But the time dimension always goes along with a spatial dimension. Why not use a 3 as exponent? This is due to the structure of the field equations for GR. We will show this in the next section.
This only achieves a shift from c and G to c and d. Swap one letter and you’re done. A clear no! We can derive the existence of the constants c and d based on our approach. There is no explanation for G. For us, G is simply the appropriate combination of c and d if you want to make a statement within spacetime. In the next section, we will see that the use of G in the field equation does not make sense at all.
Let’s take another look at the field equation of GR: G_{\mu\nu}\space =\space k\space *\space T_{\mu\nu}
The tensors G and T contain the structure of spacetime with the respective metric as the solution to the equations. The proportionality constant k does not know any metric and should therefore not have to concern itself with the structure of spacetime. Only the boundary conditions should be included. This does not depend on the metric. This is exactly how it is. The normal description of k is structured as follows:
k\space =\space \cfrac{8\space *\space \pi\space *\space G}{c^4}
We now apply our new definition to G and obtain
k\space =\space \cfrac{8\space *\space \pi\space *\space d\space *\space c^4}{c^4}\space =\space 8\space *\space \pi\space *\space d
We immediately recognize that G is not needed in the field equations. In the old description, k must be explicitly reduced by the c^4 so that G can be used there. In the metric, the time dimension is treated as a spatial dimension. The different dimensions exhibit dependent behavior as spatial dimensions only in the metric. G does not know this mutual behavior. Therefore, the c^4 in G also makes sense in this description. One c for each dimension separately.
If we eliminate G, then all limits of spacetime must still appear in the field equation. The stress-energy tensor T describes the different forms of energy. Since c is always necessary to describe energy, the low-dimensional limit is contained in T. The higher-dimensional boundary is a resistance value of spacetime independent of the distribution of spacetime density in T. Therefore, we can extract this from T and there can be a k. Only the higher-dimensional boundary can then be contained in k. This means that k is structured in line with our logic. The spacetime density generates the spacetime curvature against the resistance of spacetime.
Where does the 8π come from? If you construct the field equations mathematically, it is absolutely clear where the 8π comes from. However, the mathematical description never gives a reason and only shows how it works. We want to have a reason for everything. Here is a very simple clue:
8\space *\space \pi\space =\space 4\space *\space 2\pi
Can you remember the example comparing electrical and gravitational forces to motivate the idea that “everything is an object”? On the one hand, we have the ratio of forces and, on the other, the ratio of masses squared.
\cfrac{F_{elect}\space *\space 2\space *\space \pi}{F_{grav}\space *\space \alpha} =\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
A ratio of mass cannot directly be a ratio of forces. These are two very different perspectives on the same object. We need something like a conversion from one perspective to the other. In the example, this is 2π and α. With α, the conversion is needed for each interaction. With 2π, it is needed for each spatial dimension. The gravity between two mass points is considered a 1-dimensional connection. If we consider the entire spacetime in the field equation, we need this 4 times. When converting from the perspective of spacetime force to the perspective of gravity, 2π is probably always required for each spatial dimension. The dimensional constant d is a reciprocal value of the force. This makes the structure of k identical to our force comparison.
I have not yet been able to determine the reason behind this with 100% certainty. Currently, in 2026, everything boils down to the following explanation. The trigger for spacetime curvature must lie in our spacetime. However, the spacetime density in a black hole lies behind the event horizon. The event horizon is decisive for energy. It cannot escape from there. A geometry in our spacetime therefore does not follow a straight line to the center of the black hole, but around it. This means that 2π always comes into play in the circumference of a circle. This gives us our first point of uncertainty in the DP. Fortunately, there are only a few more. This is one of the strengths of the DP
Let’s complete our trio of explainable natural constants. We still need h. Do we even need h? We were able to generate G from c and d. We know the value of G. Then we have three equations with three unknowns. We can use them to determine the Planck values. From a physical point of view, however, we do not obtain any new information about spacetime from G. The gravitational constant is only a composition of known things. We need an additional condition from the spacetime boundary.
As the name suggests, h is a quantum of action. Let’s first ignore the part with “quantum” and concentrate on the “action.” Action means change. From one fixed state to another fixed state. Action describes a change of state. The state that we can perceive is always some form of energy, i.e., spacetime density. It is about the change in state of spacetime density. The higher-dimensional limit results from the description of GR with spacetime curvature. But the “quantum” part is certainly not included in this. No one has yet succeeded in quantizing spacetime curvature. So, let’s look at the combination of spacetime density and low-dimensional boundary. This topic will be covered in Part 3 and the description of the entire QM. Here we only consider the direct transition into our spacetime. GR describes the behavior in our spacetime with the boundaries, but not outside of spacetime.
We want to describe an effect from the low-dimensional boundary into our spacetime. Where do we start? Exactly, with a length. In DP, we only have spacetime density, and so everything must be mapped to a spatial dimension. We always need a length.
Step 1: h\space =\space l_P
Since we want to have an effect from the low-dimensional space, the boundary condition must be fulfilled. We need exactly one speed of light. Here, however, it is multiplicative and not a fraction. We want to create an effect. We can only reach our spacetime once via this boundary. The time dimension is already set to zero when a single spatial dimension is missing. This cannot be done again within spacetime. Therefore, c must not have an exponent.
Step 2: h\space =\space l_P\space *\space c
Then we still need something with which to act on the spatial dimension. We don’t have many choices in DP. It must be a form of spacetime density. It cannot be direct energy, i.e., the spacetime density in our spacetime. Here we are anticipating a later section. No time passes beyond this boundary (time definition set to zero = boundary condition), since the time dimension is always bound to the respective spacetime configuration. Let’s take another look at the definition of energy.
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
The second term cannot be it. An impulse is the increase of a given spacetime density in 3D, in one direction. This part is precisely the spacetime density in our spacetime and therefore cannot originate from a lower-dimensional spacetime. With a movement within our spacetime, we do not get very far in describing the boundary. The movement is already covered by c from step 2. So, the first term. But there is still a c there. The c is the crossing of this boundary and is already included in step 2. We have to use energy without c. This actually clarifies what mass is. A representation of a spacetime density from an n-dimensional spacetime in an (n+1)-dimensional spacetime. It is therefore not surprising that spacetime boundaries always play a role in describing the energy of a mass. We will do this more precisely in a later section. The important thing here is that we can only use the rest mass. Energy without temporal reference.
Step 3: h\space =\space l_P\space *\space m_P\space *\space c
Done! The effect from a lower-dimensional spacetime on our spacetime can only look like this. Okay, but what about the “quant” part? It could be a mapping to any length, any other speed, or any other mass. Why use the Planck values of our spacetime if the effect comes from the lower-dimensional one? In particular, we said earlier that in the lower-dimensional one, the Planck masses are explicitly different from those in our spacetime.
The limits come from GR. This describes only one spacetime, our spacetime. When we measure anything through an interaction or receive information, this happens only and exclusively in our spacetime. Energy is the spacetime density of our spacetime. Especially in, we are still at the stage where we can only recognize the spacetime density and spacetime curvature of our spacetime.
This means that any effect on a spacetime density is a change in the spacetime density in our spacetime. Thus, an effect must comply with the conditions of our spacetime, regardless of the low-dimensional spacetime configuration from which this effect originates. This is h between the boundaries c and d with the known Planck values of our spacetime. This is the structure of our spacetime. As silly as this statement may sound, the quantization of all effects does not come from QM, but from the low-dimensional boundary of our continuous spacetime.
Quantization by h results from the characteristic Planck values of our spacetime through the low-dimensional boundary.
To round this off, let’s move on to the next section and take a look at the Compton wavelength.
Why are we including the Compton wavelength here? Isn’t this a prime example of quantum mechanics? Because we need a state in addition to an effect. Unfortunately, this fact is well hidden in textbook descriptions.
The term is often referred to as the Compton effect or Compton scattering. A photon is fired at a particle with rest mass. That sounds very much like a process and not a state. The appropriate formula:
\Delta\lambda\space =\space \cfrac{h}{m_C\space *\space c}\space (1\space -\space cos\varphi)The formula describes the increase in the wavelength of the photon due to scattering. What is striking is that the state of the photon before the process is not included in the formula. Only the angle is decisive. Let’s make life easy and assume an angle of 90° for the scattering. Then the cosine is zero. The formula is simplified, and we obtain a characteristic wavelength for a mass, the Compton wavelength
\Delta\lambda\space =\space \cfrac{h}{m_C\space *\space c}This looks much simpler. The subscript C denotes the particles involved in the scattering. The equation also contains an h. This is a poor representation. The formula describes the result after the process and is therefore a description of a state.
Let’s take our new definition of h and insert it into the formula:
\lambda_C\space =\space \cfrac{h}{m_C\space *\space c}\space =\space \cfrac{l_P\space *\space m_P\space *\space c}{m_C\space *\space c}\space =\space \cfrac{l_P\space *\space m_P}{m_C}\space \implies\space \lambda_C\space *\space m_C\space =\space l_P\space *\space m_P
To make it look a little nicer, we rename \lambda_C to l_C.
l_C\space *\space m_C\space =\space l_P\space *\space m_P
This is a good result. Let’s take a look at what this formula tells us:
Anyone who was surprised that we can generate quantization from GRT will now have to grit their teeth. We’re going to take it up a notch. Take a deep breath and let’s go.
The state of a single spacetime density is fixed at l_P\space *\space m_P. The change with an h is just a different distribution on the side with the internal structure l_C\space *\space m_C. That is why h is attributed to QM. However, the definition comes from the boundary of our spacetime.
That was strong stuff, but two important properties from the boundary of spacetime are still missing. We will deal with these topics first and then return to rest mass.
In the logic presented so far, it is not 100% clear why we can recognize interface objects in our space-time. The following question arises: What properties can we recognize across a dimensional boundary? We are certain that we must be able to recognize something. In our spacetime, there are photons as objects for the lower-dimensional boundary and black holes as objects for the higher-dimensional boundary.
We will see that we can only preserve very few properties across the dimensional boundary. This runs counter to normal intuition. There are two major areas here. We will treat time as a separate area in the next section, 3.9. Here, we will deal with the geometry of objects and thus with the geometry of spacetime.
The idea that a black hole is some kind of transition is old hat. There are lots of different ideas about this. One of them, for example, is the keyword: wormhole. If you don’t look at it too strictly, the higher-dimensional transition just looks like a wormhole. In DP, into a higher-dimensional spacetime. With the ingredients black hole and transition, it’s very easy to come up with this idea. Unfortunately, the wormhole doesn’t fit. To put it bluntly, the idea of a wormhole is completely wrong.
The problem is graphics of this kind
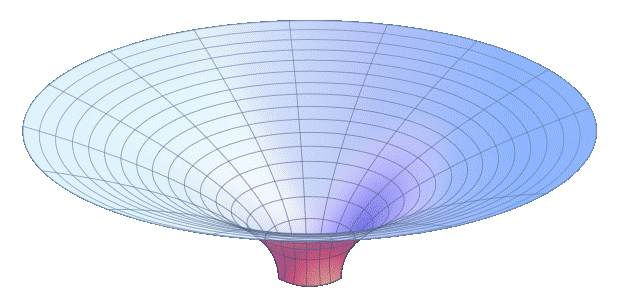
A spacetime curvature from our 3D spacetime is reduced to an image in a 1D spacetime (one spatial component radial and one temporal component diagonal). Mathematically, everything is neat with one restriction. GR does not need a higher-dimensional surrounding space for spacetime curvature. The image shows the 1D spacetime curvature explicitly with an extrinsic manifestation in 3D. According to GR, this is incorrect. However, it cannot be represented in any other way. Such an image of spacetime as a funnel is called a wormhole. The decisive factor is the “bottom” of the funnel. Where does the “hole” lead? This is precisely where the problem lies. There is no hole.
The image with the funnel leads one to believe that a wormhole is created by the curvature of spacetime. This is also the general textbook opinion in physics. Here, from the DP, a clear no! The curvature of spacetime has nothing, absolutely nothing, to do with the transition. The funnel image leads us down the wrong path. The condition for the transition is: d\space =\space \frac{l_P}{E_P}.It mentions length and spacetime density. There is no mention of spacetime curvature. Spacetime curvature is the compensation of spacetime to a spacetime density. The transition is the spacetime density and not the spacetime curvature. Okay, the transition is at the bottom of the funnel and the spacetime curvature leads there. However, spacetime curvature is not the transition. There is no singularity of spacetime curvature. In this representation, the bottom must simply be a flat disc. Spacetime curvature only extends to spacetime density. This means that the bottom is flat. It is precisely this flat bottom without spacetime curvature that must be connected to a higher spacetime.
The space-time density, and not the space-time curvature, is the reason for the higher-dimensional transition
Cross-check: If the transition lies in the spacetime curvature, then there would have to be a maximum value or a singularity for the spacetime curvature. With singularity, we have an infinite value, which cannot be a transition; it is not defined. If we have a maximum value, then the growth of a black hole would have to be limited. The spacetime curvature would then only reach this value. No more matter could fall into the black hole. There is no known growth limit for a black hole.
What can we recognize in a spacetime density that also lies in 4D? These can only be the properties from our spacetime that are connected via the transition. In the case of spacetime density, this is not much. We only recognize the properties of energy. Let’s take another look at the formula for energy:
E\space =\space \sqrt{m^2c^4\space +\space p^2c^2}
The first term is then the rest mass of the black hole. The second term is the motion of the black hole in our spacetime. There is momentum and angular momentum. That’s it, that’s all we have
Wait a minute! We are familiar with this topic. In addition to mass and intrinsic motion, a black hole also has at least one property: electric charge. The charges cannot simply disappear. This leads us directly to the information paradox of a black hole.
The first limitation on the contents of a black hole comes from the curvature of spacetime. We agree with QM that all interactions of the Standard Model without gravity can only be transmitted via exchange particles. The fastest of these is the photon. A black hole is characterized by the fact that even a photon cannot leave the event horizon. This means that no single property from QM can be known outside the event horizon.
In quantum mechanics, it is a mathematical theorem that information cannot simply disappear. Since we do not change the mathematics of quantum mechanics, but rather confirm it, we must adhere to this theorem. The fact that we humans outside the black hole can no longer access this information is not a paradox, but merely our own arrogance. This is not important.
The problem lies, for example, in Hawking radiation. The exact mechanism is not relevant here. What is important is that a black hole can release its energy through particles that were not behind the event horizon at all. The particles from the edge of the event horizon therefore do not carry any information out of the black hole. Nevertheless, the black hole loses mass and dissolves very, very slowly. Where has the information of the particles in the black hole gone?
The information is indeed no longer present at the “bottom” of the funnel. Nevertheless, we are not violating the information theorem. You can probably guess the reason. The dimensional transition. The low-dimensional transition between 3D and 2D generates the entire QM. Only at the center of a black hole are we at the transition from 3D to 4D.
The condition for a black hole is: d\space =\space \cfrac{l_P}{E_P}
The condition for a mapping across the low-dimensional boundary is:
Effect: h\space =\space l_P\space *\space m_P\space *\space c
State: l_C\space *\space m_C\space =\space l_P\space *\space m_P
The condition in d is explicitly such that we either have a length smaller than l_P or energy with a mass greater than m_P. Then we can map neither an effect nor a state in our spacetime via the low-dimensional interface. This fits very well, since the condition for a black hole is that the spacetime density can no longer be mapped in our spacetime. Then we can no longer obtain a 2D mapping for it either.
That makes perfect sense. QM is formed via the interface between 2D and 3D. In a black hole, however, we are outside of spacetime, or rather, right on the border to 4D. There is no longer a 2D representation. With the formation of a black hole, the 3D spacetime density loses its 2D representation for QM. QM is no longer applicable there and cannot make any statements about the higher-dimensional transition. There is no information paradox from QM in a black hole. QM loses its validity at the center of a black hole. There is actually no low-dimensional “inner” structure of spacetime density in a black hole. Therefore, there is no information. QM does not lose any information for itself; it is simply no longer meaningful there. In fact, the opposite is true. If Hawking radiation from a black hole were to bring out its information, then we would have a problem.
Perhaps you can guess how I feel when, time and again, the great promise is made that only QM with some kind of quantum gravity can solve the mystery of the singularity in a black hole, lol.
The exact description of the interface is the entire Part 3 of QM. Here we will only address one point. If everything is a deformation of spacetime due to density and curvature, why can’t we recognize this geometry directly from the low-dimensional? We are not saying that an elementary particle has a spacetime curvature upwards or downwards. New terms such as spin and charge are added. This suggests that it is not so easy to recognize a spacetime geometry via a dimensional transition.
The whole thing is even wilder than that. In a first approach, it is impossible to recognize any geometry at all across such a boundary. That point was almost the end of DP. It was clear that this transition would be one of the most important properties of DP. However, for a very long time, I was unable to find a geometric mapping across the boundary. In retrospect, the solution was so simple and obvious that I was really ashamed of myself. Once you have the solution, everything is very easy. But first you have to come up with it. The solution is the interface itself. From that point on, almost all other problems solved themselves. All it took was a little time and brainpower.
The real problem is not a low-dimensional transition, but fundamentally the transition with a different number of spatial dimensions. The problem exists in every n-dimensional spacetime.
Let’s start in our spacetime and imagine a volume. Length * width * height. The volume has an extension and a surface area in our spacetime. So far, so good. Now let’s take a two-dimensional surface with length * width and height = 0. One spatial dimension must be zero. That is the definition of low-dimensional. Then, by definition, the volume and surface area are also zero.
But we can specify the length, width, and area for the surface. These are good dimensions. Yes, but that is again a mathematical abstraction, similar to the discussion with the point, this time in 2D. In 3D, we cannot recognize the beginning or end of length or width. The height is zero. For us as 3D beings, there is nothing there. A 2D surface can be described mathematically in abstract terms, but it cannot be recognized in real 3D spacetime. We are no better off if we turn the surface into a sphere (a closed object). This is because the height or thickness of the surface that bounds the sphere is zero by definition. There is nothing there.
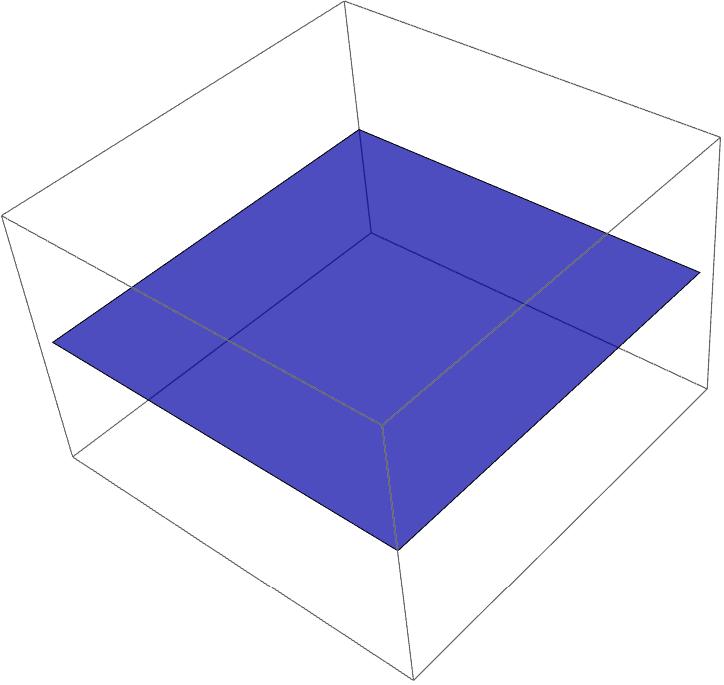
How can we recognize the surface as an object in 3D if we cannot determine the beginning or end of its length or width due to its lack of height?
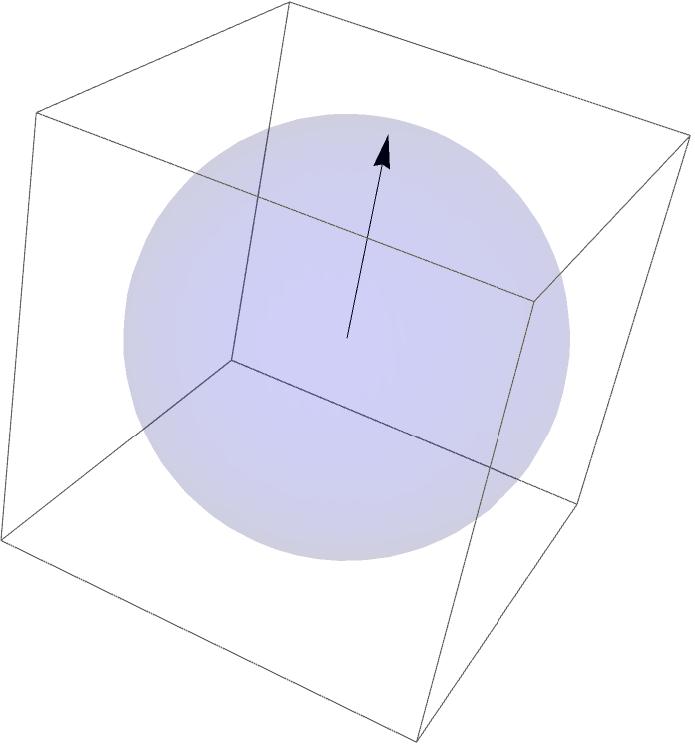
At first glance, this looks like a 3D object. But to do so, we would need to be able to determine the shell with the radius. However, the height of the shell is defined as zero. There is nothing where we can determine a radius. This means that we cannot identify this supposed 3D object in our spacetime.
We can “crumple” a surface such as a sheet of paper as we wish. The sheet of paper has a volume. Therefore, we can recognize any change in its shape. A surface has no volume and no surface area. Therefore, we cannot recognize this surface in any form.
Everyone needs to think about this separately in a quiet moment. You will come to the following conclusion:
No geometric quantity can be transmitted across the dimensional boundary.
Length, volume, surface area, or even just a distance are specifications that only correspond to meaningful geometric specifications in their own n-dimensional spacetime. It does not matter what form the lower- or higher-dimensional geometry has. This geometry is not recognizable in its own spacetime. That is very little. In Part 3, we will see that it is precisely this behavior and the lack of time from Section 3.9 that make the description of QM so “strange.”
We should be able to recognize something, otherwise our approach is wrong. However, it is not necessary to be able to recognize geometric shapes. We must be able to recognize a spacetime density. Everything is based on this.
In the textbook description of GR, spacetime curvature and thus also spacetime density are always intrinsic to spacetime. Let’s take our funnel image, Figure 3-1. It is important to note that, from a purely mathematical point of view, the image is a 100% accurate representation. Only from the perspective of GR can there be no extrinsic curvature.

This means that the spacetime curvature must lie in the plane. In the funnel, however, the spacetime curvature is explicitly drawn downwards out of the plane. This makes it an extrinsic representation and actually incorrect for GR. Really? Why does GR not want to have an extrinsic representation? This is precisely where the solution lies.
Our 3D spacetime would have to be embedded in a higher spacetime. Since we want to get by with as few additional assumptions as possible, we leave this out and make the illustrations intrinsic. This is not a problem mathematically. However, the description of GR could just as well be extrinsic. This is the application of Ockham’s razor.
Fortunately, we are in the description of the DP. The spacetime boundaries necessarily imply that our spacetime is embedded in at least one higher-dimensional spacetime, since we have black holes. The spacetime boundaries exist. It follows that we can use an extrinsic description without restriction. In Part 3, we will see that, with one exception, the rest mass, we can only recognize extrinsic properties.
Here is a false image of a 2D surface in a 3D volume. There can be as much 2D geometry in the 2D surface as you like. We cannot recognize anything. The surface is only an abstraction.


However, if we extrinsically deform the 2D surface into a wave, then the 3D volume contains more 2D spacetime. This is an increase in spacetime density in the 3D volume. There is more low-dimensional spacetime contained. This means that if we deviate from the default setting of not using extrinsic deformation, we have found a way to achieve a recognizable spacetime density.
The dimensional interface, which does not transfer any geometric properties, also means that we can use an extrinsic characteristic due to the embedding. We can recognize this characteristic in 3D. A wave representation cannot be recognized in 2D itself. It must always go through the spacetime density. This means that a photon (a representation in only two spatial dimensions) must necessarily be a wave representation. However, it is a wave representation of a single spacetime density. Particle and wave at the same time. This is not an error or a paradox; it is actually correct in this simple image. This also allows us to explain why the wavelength and not the amplitude indicates the energy for a photon. If we increase the amplitude, we would also have to increase the volume affected. The amplitude becomes larger and the height of the volume grows identically. This does not give us a greater spacetime density in a volume. Only when we push the wave crests together do we obtain more 2D area in the same volume. This is completely independent of the amplitude.
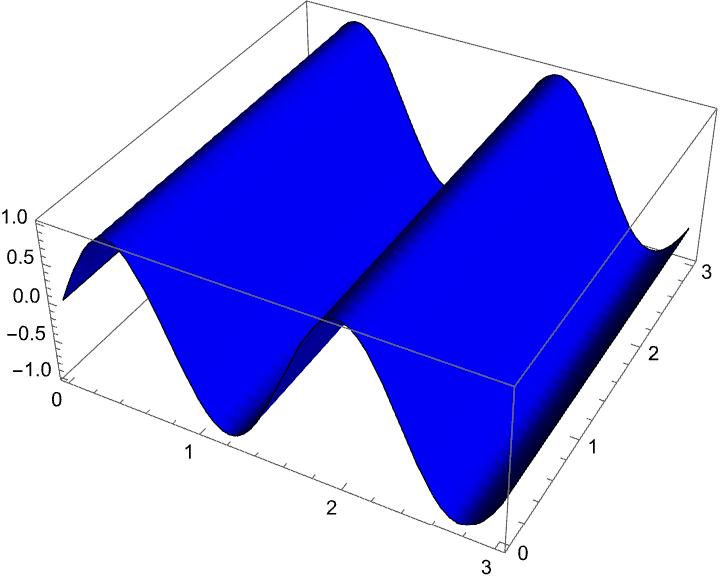
This is a very simple image (and to be precise, an incorrect image) of a photon, but we will discuss this in more detail in Part 3. The waves are traveling in the wrong direction here! The spatial dimension in the direction of the amplitude is missing. The photon would then have to move in this direction. However, this is suitable for illustrating an analogy. We have now found a possible transition for the representation of spacetime density in 3D.
Wave mapping sounds as if it is heading in the right direction for QM. For QM, we have to map the entire particle zoo of the Standard Model in low-dimensional spacetime configurations. The possibility of extrinsic mapping is a start. However, it is never sufficient for the required diversity. It’s good to know that something is still missing. But what is it? We have already looked at the solution twice and discussed it.
Drum roll, the solution is: the funnel. I won’t show the picture here, otherwise it wouldn’t be a surprise. The funnel in connection with the spacetime boundaries gave us the idea that we could use an extrinsic representation such as the funnel. Question: What object should the funnel represent? Exactly, a black hole. What is a black hole? Right, the higher-dimensional transition. We need a representation of a black hole in the lower dimension. Then we have a higher-dimensional transition from 2D to 3D and are exactly where we want to be, in our spacetime. It’s written here in this paragraph so simply. Believe me, this simple idea was a difficult birth.
This black hole is also the reason for particles with rest mass. The funny thing is that there is a small calculation about a black hole in quite a few textbooks. Please calculate why an electron cannot be a black hole. The calculation is simple and results in a Schwarzschild radius of approximately 1,353\space *\space 10^{-57} for the electron. This is smaller than the Planck length. Therefore, an electron cannot be a black hole. We will see later that this statement is absolutely correct for our spacetime. There is a minimum limit for the Schwarzschild radius. The electron falls short of this by many orders of magnitude. However, the electron is the perfect black hole in a 2D spacetime. With a much smaller dimensional constant than in this spacetime. Every spacetime has its own Planck values. We already know the Planck mass of a simple 2D spacetime, the rest mass of the electron.
The mystery of time certainly deserves more than just one section in this chapter. We can be sure that we will not solve it completely. However, we need a suitable logical description of time for the DP. This is discussed here because in the DP, time can only be understood in connection with the spacetime boundary.
Time is always associated with change. Without change, time could not be recognized, and vice versa. In DP, everything we can recognize is associated with at least one spatial dimension. To be able to map a density, we need at least one spatial dimension. A change in a mapping is therefore always a change in spatial dimension and time. Time and space are therefore not independent.
We have already started with an approach from GR. It is therefore clear that we must work with spacetime as an inseparable object. Nevertheless, it makes sense to derive this unity as a consequence of a density on the spatial dimension. Since space and time are not independent, we will stick with spacetime and spacetime density.
However, the question remains as to why time does not simply pass at a constant rate when the density of space changes. This is because a change in the density of space is a change in the definition of space. Speed is length divided by time. Time remains the same, but length becomes “shorter” when acceleration occurs. The object would slow down during acceleration. This does not correspond to observation. The calculations of GR only work because the time dimension has been turned into a spatial dimension. Again: in GR, as in SR, the time dimension is a spatial dimension with different signs. The definition of geometry changes in the spatial dimension. This means that the time dimension, as the definition of time, must also change. The spatial and time dimensions change the definition of what a unit of length or a unit of time is. Nothing is squeezed or stretched.
Time is thus bound to the spacetime configuration. If this configuration changes, for example, if there is one less spatial dimension, then this is no longer the same spacetime. The object spacetime is abandoned. Then time must also run towards zero. Therefore, each spacetime configuration must have its own time dimension.
From this, we can deduce the following:
From the perspective of time, the spacetime boundaries are reached when we can no longer achieve any effect on a state, no further change. Then we can no longer determine time. Let’s take another look at the small formulas for effect and state in our spacetime:
Effect: h\space =\space l_P\space *\space m_P\space *\space c
State: l_C\space *\space m_C\space =\space l_P\space *\space m_P
Let’s take only the right side in each case and put the effect in relation to the state:
\cfrac{State}{Effect }\space =\space \cfrac{l_P\space *\space m_P}{l_P\space *\space m_P\space *\space c}\space \cfrac{1}{c}
This is the “resistance value” of spacetime against change. It is bridged at c and no further change can occur. The effect from the lower dimension must still be able to change the state mapping from the lower dimension. This is the lower-dimensional boundary.
From these considerations, we can equate time with the distance to the boundaries of spacetime.
Time is a measure of distance to the spacetime boundary
Thus, in DP, there is no flow of time or arrow of time. The better view is that the experience of time is the constant measurement of distance to the spacetime boundary. Therefore, we do not experience the past. The next measurement to the boundary always comes. The “measured value (the definition of the unit of time)” can repeat itself from the past. However, it is a different measurement. The flow of time is the series of distance measurements.
Finally, a frequently asked question: Why is there only one time dimension? This question can be easily explained with our new perspective. The object spacetime can be left exactly once. Then you are out. We cannot leave spacetime again once we are already outside. Therefore, there can only be one time dimension. The passage of time is the distance measurement to the spacetime boundary. Only one time dimension per spacetime is possible.
The idea that time is a distance measurement has another reason: the principle of relativity. This explains very well why time remains constant locally. This will be worked through in the next chapter.
There are separate values for each elementary particle for rest mass, unlike h, which has one value for all. Of course, h comes from the interface and simply applies to everything from the low-dimensional. Rest mass is a low-dimensional spacetime density. Rest masses are also a quantum in themselves. For each particle/spacetime configuration, there is only one specific value and then a multiple of that.
Each spacetime configuration has its own Planck values, and in 2D, every image we perceive in 3D with rest mass is an image with at least one black hole. The rest mass for an electron in 2D is the Planck mass for the dimensional constant there. The rest mass is the energy or spacetime density without the temporal component.
Let’s look at this with some mathematics. For the rest mass, we can again use the most famous formula in the world: E\space =\space mc^2. If we want to turn the rest mass into energy in our spacetime, we always have to insert a c^2. WWhy is that? I hope that no one will now come up with the idea that “well, the formula specifies this.” Yes, the formula does, and the units of measurement must match. We have to explain why we use c^2 based on the logic of DP. As always, this results from the interface. The superposition of 3D to 2D is only in space. This means that in the first step, we have only occupied two spatial dimensions. Since the dimensional constant was exceeded in 2D, more spatial dimensions are required for the mapping. However, energy and thus spacetime density in our spacetime must occupy all three spatial dimensions and the time dimension. The transition is always one spatial dimension and one time dimension. The time dimension is a “disguised” spatial dimension. Since we have to create the “transition” for this, we need one c per spatial dimension and end up with c^2. So, we always have to multiply by a c^2. The logic is correct for spacetime of any dimension, since we only ever create the transition to a spatial dimension higher n+1 or lower n-1. Even with one spatial dimension, we can more or less no longer recognize any properties. With two more spatial dimensions, we can no longer recognize anything at all. With two fewer spatial dimensions, it is only possible via a detour, which we will use for neutrinos. Therefore, E\space =\space mc^2 is universally valid for all arbitrary spacetimes.
A word about the units of measurement for energy, force, and effect. First, let’s write down the units of measurement for the three values:
The way we write the units of measurement alone indicates a certain direction in which to read them. We have just clarified energy, and that is why the units of measurement look like this. We could also have written energy as follows: [kg\space *\space m\space *\space\cfrac{m}{s^2}\space]. Then it looks as if energy involves acceleration and thus a perpetual rate of change. This is somewhat strange for a quantity that cannot change itself. With our logic, the interpretation of the units of measurement is fixed. With force, something is explicitly changed. When specifying force, the change is given as acceleration, i.e., as a rate of change. With effect, the units of measurement arise because it is actually energy * time, and therefore the time in the denominator of cancels out. In other words, a continuous portion of energy over a period of time. There must be no acceleration. It is the change from one state to a new state. Since the rest mass cannot change, it is always a change in momentum. The effect therefore also includes momentum: [kg\space *\space \cfrac{m}{s}\space]. How this momentum is distributed over a length is then the effect. If the momentum is distributed over a short length, then the effect is large, and vice versa. We want to explain everything here. We cannot afford to use the normal procedure in physics, where we set G (at and d), h, and c to 1 and then adjust everything later in the result so that the units of measurement are correct. This only works when calculating without thinking, but not when explaining.
Can we calculate the Planck values in a spacetime configuration? Yes and no. Without a further assumption for the calculation, we will not get anywhere. The Planck values per spacetime configuration are simply given. In 2026, I have not yet found a way to calculate them. However, we can perform a calculation by anticipating a later topic. The anticipation is that we will consider electromagnetic force as low-dimensional gravity. In addition, it should be noted once again that we can only determine a rest mass from 2D in our 3D spacetime with the values known to us. In 2D itself, this looks different again.
Let’s take something we know: the comparison of the forces of gravity and the electric field. I’ll write down the solution.
\cfrac{F_{elec}}{F_{grav}}\space =\space \cfrac{\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space r^2}}{\cfrac{G\space *\space m_1\space *\space m_2}{r^2}}\space =\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space G\space *\space m_e^2}\space =\space 4\space *\space 10^{42}\space = \bigg(\cfrac{1}{2\space *\space \pi}\bigg)\space *\space \alpha\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
The terms on the right-hand side do not include gravity or an electric field. Nevertheless, the values are identical. How is that possible? Assuming that gravity as a force and the electric field as a force differ only in the number of dimensions, this comparison should only depend on the difference in the Planck values and the low-dimensional transition. This is exactly what we see here.
The mathematical explanation is very simple. Let’s take the term in the middle:
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space G\space *\space m_e^2}
Step 1: We write our definition of G into the formula.
\cfrac{e^2\space *\space m_P}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_e^2}
Step 2: We expand the fraction with a Planck mass m_P.
\cfrac{e^2\space *\space m_P^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_P\space *\space m_e^2}\space =\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c^2\space *\space m_P}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Step 3: We pull the c^2 apart and take a closer look at the denominator.
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space l_P *\space c\space *\space c\space *\space m_P}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Step 4: There is now an h\space =\space l_P\space *\space m_p\space *\space c hidden in the denominator.
\cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space h\space *\space c}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
Step 5: Then the first term is almost the fine structure constant \alpha. However, we have an h and no \hbar. Therefore, we must expand the whole thing with 2\space *\space \pi.
\cfrac{1}{2\space *\space \pi}\space *\space \cfrac{e^2}{4\space *\space \pi\space *\space \epsilon_0\space *\space h\space *\space c}\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2\space =\space \bigg(\cfrac{1}{2\space *\space \pi}\bigg)\space *\space \alpha\space *\space \bigg(\cfrac{m_P}{m_e}\bigg)^2
These were all very simple mathematical transformations. If we want to know what this means, we have to stop calculating and move on to an explanation.
Let’s roll up the field from the back and start with the term (\frac{m_P}{m_e})^2. The square arises because, when comparing forces, we compare the force between two objects in the respective spacetime. Therefore, we have to put a square here. Why is the Planck mass in the numerator and the rest mass of the electron in the denominator? When comparing forces, we did the opposite. When comparing forces, the force from the electric field is much greater because electrons are much more easily influenced in their spacetime. If we apply the ratio to spacetime itself, then of course our spacetime is much stronger/tougher than 2D spacetime. Therefore, the ratio must be reversed.
We capture the fine structure constant \alpha because we are comparing forces to the electric field. The exact explanation will come in part 3. Here is the short version: \alpha behaves like a scale adjustment on a map. The scale must simply be shortened by \alpha can only refer to the speed of light. Since the speed of light does not depend on the number of spatial dimensions, length contraction and time dilation only affect the direction of motion without taking the remaining spatial dimensions into account, so the fraction from \frac{l_P}{t_P} must be achieved with values that differ from \alpha. The speed of light is a fraction and can be achieved with an infinite number of values. However, since the speed of light c is the dimensional transition, \alpha must play a role in every interaction with an electric charge. In the case of multiple interactions, this occurs with an exponent. We will take a closer look at this in Part 3.
2\space *\space \pi is an old acquaintance of ours from the field equation. When we work with a force in our space-time, we need it for each spatial dimension. Since we always have a connecting line between the objects in a force, 2\space *\space \pi only occurs once here. Since we have reversed the ratio, we need them in the denominator here.
That was a lengthy section on rest mass, units of measurement, and the “toughness” of the spacetime configuration. These small notes serve to better understand the topic of dimensional transition. At the end of the chapter, let’s turn to a completely different topic.
In the last section, let’s look at a specific effect of the boundaries of spacetime. If there is any truth to the idea of a very hard boundary of spacetime, most other “Theories of Everything (ToE)” or interpretations of quantum mechanics have a big problem. Almost all of them no longer work.
We can divide the mainstream approaches to these theories into four categories:
For each of these categories as to why this cannot work. This makes it clear how popular DP is among physicists. We can probably rule out over 95% of all approaches for which these physicists receive research grants in this field. Here, we have to grin and bear it. This is not about labeling other theories as “bad.” If we can rule out these theories, then we have found tests for DP. The fundamental characteristics of these theories are tough tests for the DP. Let’s just go through the categories.
Here we have two killer arguments as to why this can no longer work. In the DP, energy is also the state of motion. This means that spacetime must have two compelling properties: it must be continuous and differentiable. Otherwise, we cannot map motion as spacetime geometry directly in spacetime. A spacetime in quanta is therefore not possible. In particular, in all other theories, spacetime and the content of spacetime are separate descriptions. Spacetime is only used as a “background.” Then one could still imagine quantization. But if motion is a geometry of spacetime itself, this no longer works.
The second argument is the boundary itself as we have defined it in DP. This can only be the speed of light and a black hole. How can spacetime, usually on the length of Planck scales, be divisible into pieces? Then every spacetime quantum either travels at the speed of light and can no longer determine time, or it is a black hole. We can confidently rule out both variants. Quantization of spacetime is not possible with the DP approach.
What we do with the boundary of spacetime is that we separate complete spacetimes very strictly from one another. For us, a single spacetime is a piece/object. However, we cannot further divide a single spacetime.
If quantization of spacetime is ever detected, the DP will be falsified.
Here we must anticipate somewhat in the areas of cosmology and QM. We will find there that exchange particles can only exist between spacetimes that are embedded in at least one higher-dimensional spacetime. Exchange particles, in turn, can only be images in an embedded spacetime. Spacetime curvature is explicitly a description in its own spacetime. The spacetime curvature does not change the spacetime density. This means that there is also no change in the lower-dimensional images. We do not obtain an image of the spacetime curvature across a spacetime boundary. As a reminder, the transition always lies in the spacetime density and not in the spacetime curvature. With our approach, we cannot break down gravity into quanta.
If quantum gravity is ever discovered, the DP will be falsified.
A many-worlds interpretation of QM sounds very much like DP. We have separate spacetimes. We have as many spacetimes as there are possibilities. We do the same thing in DP. At the level of keywords, this is all correct. In detail, however, we do something completely different in DP.
We only ever have a multitude of spacetimes via the lower-dimensional spacetimes. If our universe is a 3D spacetime, then in a measurement process in QM, an exact selection is made from a set of 2D spacetimes. This mapping from 2D produces an effect in our spacetime via the lower-dimensional boundary. We do not create worlds of equal dimensions in a measurement process. We reduce all 2D possibilities to the one that carries out the interaction. In cosmology, we will then see that a 2D spacetime is very different from our 3D spacetime. We do not have the idea that I exist in another universe where I declare DP to be nonsense. I exist only once in our universe and I do not exist in other 3D universes.
With the Higgs boson, we will also obtain an infinite number of 3D universes in the DP. However, these are not created by a measurement or similar. They already exist in our universe since the Big Bang and can only communicate via the Higgs boson.
If a many-worlds interpretation is ever established, the DP will be falsified.
Here we have a similar situation. In the DP, we claim that low-dimensional and higher-dimensional spaces exist explicitly. In string theory, we have a different number of spatial dimensions depending on the configuration. Then there is the AdS/CFT correspondence. There, gravity is mapped one spatial dimension higher than the particles of QFT. The black holes in the lower dimension must also be an AdS spacetime in DP. It looks damn similar. Ultimately, for the mapping of a neutrino, we will have a structure with exactly one spatial dimension. That’s a string!
I find it amazing how many similarities there are in certain aspects between the different approaches of the respective theories. But the theories work fundamentally differently. In DP, we can’t do anything with any version of string theory. Let’s take three points.
DP and any form of string theory are mutually exclusive.
If a variant of string theory is ever discovered, DP will be falsified.
If a supersymmetric particle is ever found to be an elementary particle, DP is falsified.
If a compactified spatial dimension is ever found, DP is falsified.
That was a lot of points to consider. All of them stem from the limitations of spacetime. These limitations make DP possible in the first place, but they rule out virtually all other approaches.
With that, we will finally close this now very long chapter. Next, we will build one of the most important foundations of physics, the principle of relativity.